III уровень

3.1.Постройте эмпирическую функцию распределения и ее график для выборки:

xi	2	5	7	10
ni	5	25	15	5

3.2.Постройте гистограмму относительных частот для выборки:

Вариант i	Интервал	ni
1	(10; 15)	2
2	(15; 20)	4
3	(20; 25)	8
4	(25; 30)	4
5	(30; 35)	2

3.3.Постройте дискретный вариационный ряд и начертите полигон для следующего распределения размеров 45 пар мужской обуви, проданных магазином за день:

39 41 40 42 41 40 42 44 40 43 42 41 43

39 42 41 42 39 41 37 43 41 38 43 42 41

40 41 38 44 40 39 41 40 42 40 41 42 40

43 38 39 41 41 42.

3.4.Определение жирности молока (в %) от 25 коров дало следующие результаты:

3,45 3,56 3,68 3,66 3,70 3,76 3,75

3,78 3,80 3,94 3,88 3,86 3,88 3,94

3,93 3,90 3,96 4,03 4,03 3,98 4,00

4,08 4,10 4,18 4,35.

Выбрав за длину интервала h = 0,10 %, составьте интервальную таблицу частот; постройте гистограмму.

3.5.Постройте гистограмму относительных частот по заданному распределению выборки:

Номер интервала i	Частичный интервал xi – xi + 1	Сумма частот вариант частичного интервала ni
1	10–15	2
2	15–20	4
3	20–25	8
4	25–30	4
5	30–35	2

3.6.Напряжение тока в электросети измерялось через каждый час. При этом были получены следующие значения (в вольтах):

Постройте статистическое распределение и начертите полигон.

32.2. Точечные и интервальные оценки

параметров распределения

Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится извлеченным значениеxпризнакаXэтого объекта. Таким образом, можно рассматривать извлечение объекта из генеральной совокупности как испытание,X– как случайную величину, аx– как одно из возможных значенийX.

Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного нахождения) параметров, которыми определяется это распределение.

Обычно в распоряжении имеются лишь данные выборки генеральной совокупности, например, значения количественного признака x₁,x₂, …,x_n, полученные в результатеnнаблюдений. Через эти данные и выражается оцениваемый параметр.

Опытные значения признака Xможно рассматривать и как значения разных случайных величинX₁,X₂, …,X_nс тем же распределением, что иX, и, следовательно, с теми же числовыми характеристиками, которые имеетX. Значит,иВеличиныX₁,X₂, …,X_nможно считать независимыми в силу независимости наблюдений.

Систему случайных величин X₁,X₂, …,X_nназываютвыборкой. Функцию f(X₁,X₂, …,X_n) от наблюдаемых случайных величинX₁,X₂, …,X_nназываютстатистикой. Статистической оценкойнеизвестного параметратеоретического распределения называют статистику, значения которой близки к.

Точечной называется статистическая оценка, которая определяется одним числом гдеx₁, x₂, …, x_n – результаты n наблюдений над количественным признаком (выборка).

К оценке предъявляются следующие требования.

1.

Оценка, удовлетворяющая такому условию, называется несмещенной.

2. Для любого

Оценку, обладающую такими свойствами, называют состоятельной.

Если m– неизвестное математическое ожидание случайной величиныX, то в качестве оценкиmприменяется выборочная средняяравная

Выборочная средняя являетсянесмещенной и состоя­тельной оценкой m.

Если же значения признака x₁, x₂, …, x_k имеют соответственно частотыn₁, n₂, …, n_k, причемn₁ + n₂ + … + n_k= n, то

Отметим, что если варианты x_i – большие числа, то для упрощения вычисления выборочной средней применяют следующий прием. Пусть C – константа. Так как то

Константу C(ложный нуль) берут такой, чтобы разностиx_i – Cбыли небольшими.

В качестве оценки неизвестной дисперсии Dслучайной величиныXприменяетсявыборочная дисперсия

Выборочная дисперсия D_Bявляетсясостоятельной, но смещенной оценкой дисперсии D. Несмещенной и состоятельной оценкой D является исправленная выборочная дисперсия

При малом объеме выборки пользуются исправленной выборочной дисперсиейS²; при больших n практически безразлично, какой из двух оценок (D_B или S²) пользоваться.

Если значения признака x₁, x₂, …, x_kимеют соответственно частотыn₁, n₂, …, n_k, причемто

Более удобна формула

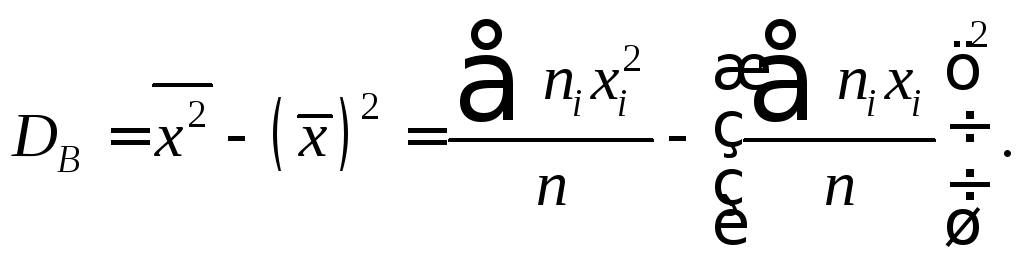
Если варианты x_i – большие числа, то для упрощения вычисления выборочной дисперсии D_B формулу приводят к следующему виду:

где C– ложный нуль.

Выборочным средним квадратическим отклонениемназывается квадратный корень из выборочной дисперсии:

Обычным эмпирическим моментом порядканазывают среднее значение-х степеней разностей

где – объем выборки;

–частота варианты;

–наблюдаемая варианта;

–произвольное постоянное число (ложный нуль).

Начальным эмпирическим моментом порядка называют обычный момент порядкапри

В частности,

Центральным эмпирическим моментом порядка называют обычный момент порядкапри

В частности,

Метод моментов точечной оценкинеизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.

Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент к одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка к начальному эмпирическому моменту первого порядка: Учитывая, чтоиполучают

Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение относительно неизвестного параметра, тем самым получают его точечную оценку.

Если распределение определяется двумя параметрами, то приравнивают два теоретических момента к двум соответствующим эмпирическим моментам того же порядка. Например, можно приравнять начальный теоретический момент первого порядка к начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка к центральному эмпирическому моменту второго порядка:

Учитывая, что приходят к системе уравнений

Решив эту систему относительно неизвестных параметров, получают их точечные оценки.

Всюду выше неизвестный параметр оценивался одним числомТакая оценка называетсяточечной. При большом числе опытов точечная оценка, как правило, близка к неизвестному параметру. Если же число наблюдений мало, то случайный характер величиныможет привести к значительному расхождению междуи. Тогда возникает задача о приближении параметране одним числом, а целыминтерваломтак, чтобы вероятность поглощения этим интервалом параметра, т. е. вероятность двойного неравенства

была не меньше заданного числа .

Интервал называетсядоверительным для параметра с доверительной вероятностью (надежностью) если неравенствовыполняется с вероятностью, не меньшей чем, т. е.

Концы идоверительного интервала называютсядоверительными границамидля оцениваемого параметра.

Интервальной оценкой (с надежностью ) математического ожидания a нормально распределенного количественного признака Xпо выборочной среднейпри известном среднем квадратическим отклонениигенеральной совокупности служит доверительный интервал

где – точность оценки,t– значение аргумента функции ЛапласаФ(t), при котором n– объем выборки. При неизвестном(и объеме выборкиn < 30)

где находят по таблице значенийпо заданнымnи (прил. 4),

S– исправленное выборочное среднее квадратическое отклонение.

Интервальной оценкой (с надежностью ) среднего квадратического отклонения  нормально распределенного признака Xпо исправленному выборочному среднему квадратическому отклонениюSслужит доверительный интервал

при q < 1,

при q > 1.

q находят по таблице значений по заданнымn и  (прил. 5).

Интервальной оценкой (с надежностью ) неизвестной вероятности p биномиального распределенияпо относительной частотеwслужит доверительный интервал

где

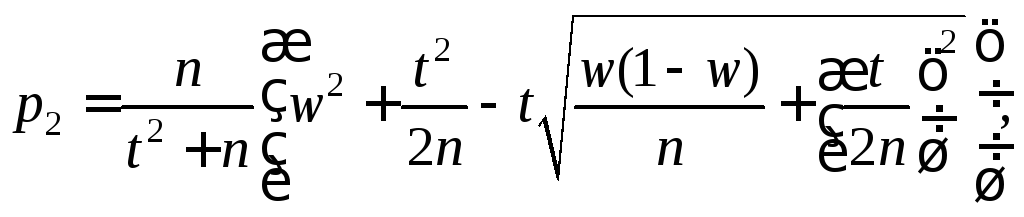
где – относительная частота;

n – общее число испытаний;

m – число появлений события;

t – значение аргумента функции Лапласа, при котором ( – заданная надежность).

При больших значениях n (порядка нескольких сотен) можно принять в качестве приближенных границ доверительного интервала величины

Пример 1. Выборочная совокупность задана таблицей распределения:

xi	1	2	3	4
ni	20	15	10	5

Найти выборочную дисперсию.

Решение. Производим вычисления:

Пример 2. Имеется выборка:

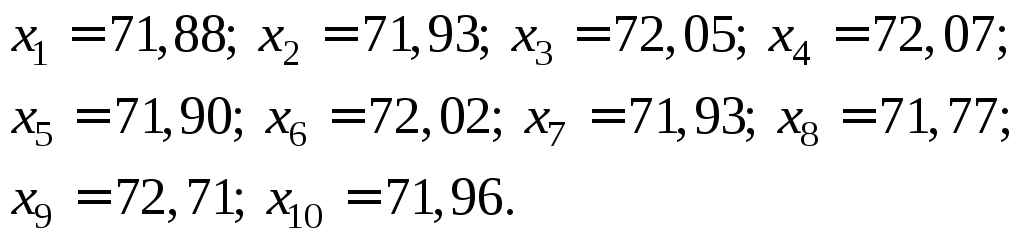
Найти выборочную дисперсию.

Решение. Возьмем ложный нуль Вычислим разности

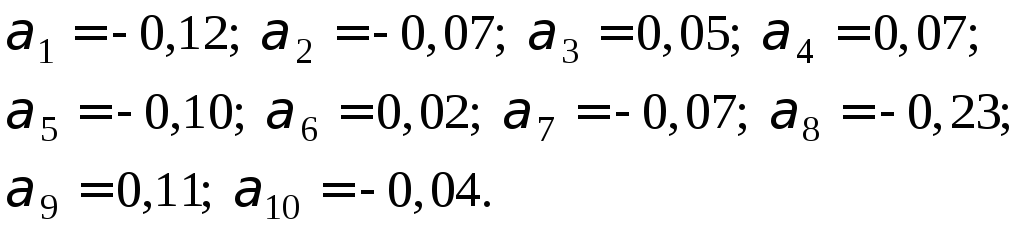
Их сумма:

их среднее арифметическое:

Выборочная средняя:

Наконец, согласно формуле получим

Пример 3. Пусть дисперсия нормально распределенной случайной величины X равна 0,25. По выборке объема найдена выборочная средняяНайти доверительный интервал по неизвестному математическому ожиданиюm, если доверительная вероятность должна быть равна 0,95.

Решение. Решим уравнение используя таблицу значений функции Лапласа (прил. 2). Дляt получим значение 1,96. Затем найдем концы доверительного интервала:

Таким образом, (51,804; 52,196) – искомый доверительный интервал с надежностью 0,95, т. е.

Задания