III уровень

3.1.Непрерывная случайная величинаХраспределена равномерно в интервале (3; 9). Найдите вероятность событияОцените вероятность событияА, используя неравенство Чебышева.

3.2.Случайная величинаХзадана функцией распределения

С помощью неравенства Чебышева оцените вероятность события Найдите

3.3.От числа посаженных саженцев приживаются в среднем 70 %. Определите, сколько нужно посадить саженцев, чтобы с вероятностью, не меньшей 0,9, ожидать, что отклонение числа прижившихся саженцев от математического ожидания не превышает по модулю 40. Решите задачу с помощью:

1) неравенства Чебышева;

2) интегральной теоремы Муавра–Лапласа.

3.4.Для определения средней урожайности поля в 5000 га предлагается взять выборку по 1 м²с каждого гектара площади и точно посчитать урожайность на этих квадратных метрах. Оцените вероятность того, что средняя выборочная урожайность будет отличаться от истинной средней урожайности на всем массиве не более чем на 0,2 ц, если предположить, что среднее квадратичное отклонение урожайности на каждом гектаре не превышает 5 ц.

3.5.Изготовлена партия деталей. Среднее значение длины детали равно 20 см, а среднее квадратичное отклонение равно 0,1 см. Оцените снизу вероятность того, что длина случайно отобранной детали находится в пределах от 19,6 до 20,4 см.

3.6.Общая стоимость всех букетов в цветочном киоске составляет 18 000 денежных единиц. Вероятность того, что стоимость взятого наудачу букета не превышает 300 денежных единиц, равна 0,7. Оцените количество букетов в киоске.

3.7.Вероятность того, что покупателю обувного магазина необходимы туфли 41-го размера, равна 0,15. Оцените границы процента покупателей среди 2000 побывавших в магазине, кото­рым нужны такие туфли, если эти границы надо гарантировать с вероятностью 0,98.

3.8.Известно, что случайная величинаХимеет плотность распределения

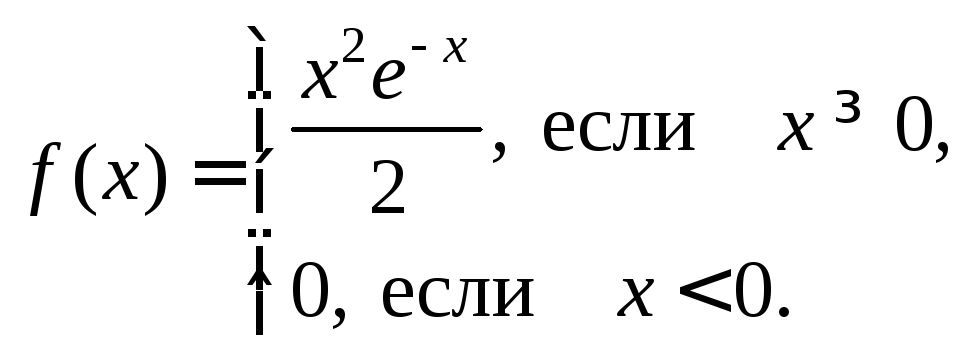
Используя неравенство Чебышева, оцените вероятность события

32. Математическая статистика

32.1. Основные понятия математической

статистики. Выборочный метод

Пусть требуется изучить множество однородных объектов (это множество называется статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Лучше всего провести сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным принципам это сделать невозможно.

Если сплошное обследование невозможно, то из генеральной совокупности для изучения выбирают часть объектов.

Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью.

Множество объектов, случайно отобранных из всей совокупности, называется выборочной совокупностью, или выборкой.

Число объектов генеральной совокупности и выборки называется соответственно объемом генеральной совокупности и объемом выборки.

Для того чтобы по данным выборки уверенно судить об интересующем нас признаке генеральной совокупности, необходи­мо, чтобы объекты выборки правильно его представляли. Дру­гими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).

Пусть для изучения количественного (дискретного или непрерывного) признака Xиз генеральной совокупности извлечена выборкаx₁,x₂, …,x_kобъемаn, причемx₁наблюдаласьn₁раз,x₂–n₂раз, …,x_k–n_kраз иn₁ + n₂ +…+ n_k=n– объем выборки. Наб-людаемые значенияx_iпризнакаXназываютвариантами, а последовательность вариант, записанная в возрастающем порядке,называется вариационным рядом. Числа наблюдений n₁, n₂, …,n_kназываютчастотами, а их отношения к объему выборки–относительными частотами. Отметим, что сумма относительных частот равна единице:

Статистическим распределением выборкиназывают перечень вариантx_iвариационного ряда и соответствующих им частот или относительных частот.

Если на плоскости в прямоугольной системе координат построить точки (x_i;n_i), (x_i;w_i) и последовательно соединить их отрезками прямых, то получим ломаную, которая называетсяполигоном частот (полигоном относительных частот).

Полигон частот дает приближенное наглядное представление о характере распределения случайной величины X.

Если изучаемая случайная величина Xнепрерывна, то вместо обычного (дискретного) вариационного ряда составляютинтервальный вариационный ряд: находят минимальную и максимальную варианты выборки и весь промежуток между ними разбивают на частичные промежутки в количестве 1–2 десятков. Получается интервальный вариационный ряд:

Далее по выборке находят n_i– сумму частот вариант, попавших вi-й интервал и– относительную частоту попадания значенийXвi-й интервал.

Если при этом некоторое значение x_kвыборки совпадает с пограничной точкой между промежутками, то его относят к правому промежутку.

Интервальная таблица частот (относительных частот) графически изображается гистограммой частот (гистограммой относительных частот).

Гистограмма частот представляет собой ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы, а высоты h_iтаковы, что площадь частичногоi-го прямоугольника равна частотеn_i. По построению суммарная площадь всех прямоугольников гистограммы равна объему выборкиn.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы, а высоты h_i таковы, что площадь i-го прямоугольника равна w_i – относительной частоте вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.

Эмпирической функцией распределения (функцией распределения выборки)называют функциюF^*(x), определяющую для каждого значенияxотносительную частоту событияX < x:

где n_x– число вариант, меньшихx; n– объем выборки.

Свойства эмпирической функции

1. Значения эмпирической функции принадлежат отрезку [0; 1].

2.F^*(x) – неубывающая функция.

3.Еслиx₁– наименьшая варианта, аx_k– наибольшая, тоF^*(x) = 0 прииF^*(x) = 1 при

Пример 1. При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка:

10 13 10 9 9 12 12 6 7 9

8 9 11 9 14 13 9 8 8 7

10 10 11 11 11 12 8 7 9 10

14 13 8 8 9 10 11 11 12 12

Составить: 1) вариационный ряд; 2) таблицу относительных частот.

Решение. 1) Выбирая различные варианты из выборки и располагая их в порядке возрастания, получим вариационный ряд:

6, 7, 8, 9, 10, 11, 12, 13, 14.

2) Для нахождения относительных частот предварительно подсчитаем для каждой варианты соответствующие частотыn_i: n_i = 1, 3, 6, 8, 6, 6, 5, 3, 2.

Получаем следующую таблицу относительных частот.

Варианта xi	6	7	8	9	10	11	12	13	14
Относительная частота wi

Пример 2. Построить полигон следующего распределения:

Варианта xi	1	2	3	5
Относительная частота wi	0,4	0,2	0,3	0,1

Решение. Полигон данного распределения изображен на рис. 32.1.

Рис. 32.1

Пример 3. Найти эмпирическую функцию по заданному распределению выборки:

Варианта xi	1	5	8
Частота ni	10	15	25

Решение. Найдем объем выборки: Наименьшая варианта равна единице, поэтомуF^*(x) = 0 при

Значение X < 5, а именно x₁ = 1, наблюдалось 10 раз, следовательно, при

Значения x < 8, а именно: x₁ = 1 и x₂ = 5, наблюдались 10 + 15 = 25 раз, следовательно, при

Так как x = 8 – наибольшая варианта, то F^*(x) = 1 при x > 8.

Напишем искомую эмпирическую функцию:

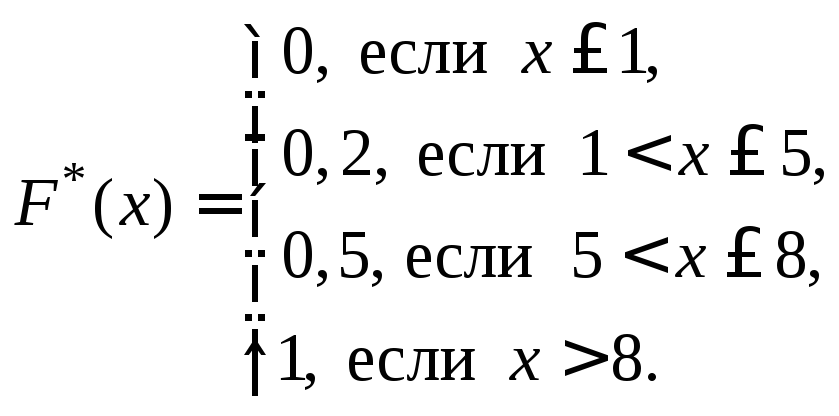
График этой функции изображен на рис. 32.2.

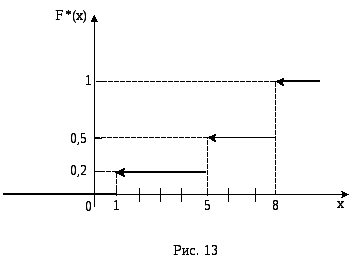
Рис. 32.2

Пример 4. Построить гистограмму относительной частоты по данному распределению выборки:

Номер интервала i	Частичный интервал xi – xi + 1	Сумма частот вариант частичного интервала ni
1	0–2	20
2	2–4	30
3	4–6	50

Решение. Найдем относительные частоты:

Найдем плотности относительных частот, учитывая, что длина интервала h = 2:

Построим на оси абсцисс данные частичные интервалы. Изобразим над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям относительной частоты. Например, на интервале (0; 2) построим отрезок, параллельный оси абсцисс и находящийся от нее на расстоянии, равном 0,1. Аналогично строим остальные отрезки.

Искомая гистограмма относительных частот изображена на рис. 32.3.

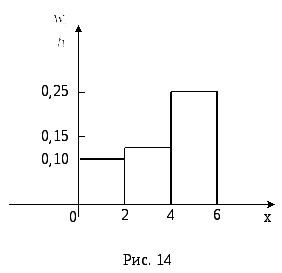
Рис. 32.3

Задания