32.3. Статистическая проверка

параметрических гипотез

Статистическойназывается гипотеза о предполагаемом виде неизвестного распределения или о параметрах известных распределений.

Нулевой (основной) называется выдвинутая гипотеза

Конкурирующей (альтернативной)называется гипотезакоторая противоречит нулевой.

Простойназывается гипотеза, содержащая только одно предположение. Гипотеза, состоящая из конечного или бесконечного числа простых гипотез, называетсясложной.

Гипотезу проверяют на основании выборки, полученной из генеральной совокупности. Из-за случайности выборки в результате проверки могут возникать ошибки и приниматься неправильные решения. В принципе возможны ошибки первого и второго рода.

Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза. Вероятность ошибки первого рода называется уровнем значимости и обозначается через . Вероятность ошибки второго рода обозначается через .

Критериемназывается случайная величинаK, которая служит для проверки нулевой гипотезы

Наблюдаемым (эмпирическим)значениемназывается то значение критерия, которое вычислено по выборкам.

Критической областьюназывается совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений)называется совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки статистических гипотез:если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Критическими точками (границами) называются точки, отделяющие критическую область от области принятия гипотезы.

Правостороннейназывается критическая область, определяемая неравенствомгде– положительное число.

Левостороннейназывается критическая область, определяемая неравенствомгде– отрицательное число.

Двустороннейназывается критическая область, определяемая неравенствами гдеВ частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенствами (в пред­положении, чтоили равносильным неравенством

Для отыскания критической области задают уровень значимости  и ищут критические точки из следующих соотношений:

а) для правосторонней критической области

б) для левосторонней критической области

в) для двусторонней симметричной области

Мощностью критерияназывается вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.

Часто распределение случайной величины известно, и по выборке наблюдений необходимо проверить предположение о значении параметров этого распределения. Такие гипотезы называются параметрическими, а методы проверки параметрических гипотез –параметрическими критериями.

Если при увеличении объема выборки вероятность стремится к единице, то такой статистический критерий называетсякритерием согласия. Критерий согласия проверяет, согласуется ли наблюдаемое распределение с гипотетическим распределением. Критерий, не использующий предположения о распределении, называетсянепараметрическим. Критерий согласия относится к непараметрическим критериям.

Пусть по независимым выборкам, объемы которых n₁иn₂, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсиииНеобходимо сравнить эти дисперсии.

Правило 1.Чтобы при заданном уровне значимостипроверить нулевую гипотезуо равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезенадо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей исправленной дисперсии)

По таблице критических точек распределения Фишера–Сне­декора (прил. 6), по заданному уровню значимости  и числам степеней свободы (k₁ – число степеней свободы большей исправленной дисперсии) необходимо найти критическую точку Если– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе :критическую точкуищут по уровню значимости(вдвое меньше заданного) и числам степеней свободыk₁иk₂(k₁– число степеней свободы большей дисперсии). Если– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Сравнение исправленной выборочной дисперсии

с гипотетической генеральной дисперсией

Правило 1.Чтобы при заданном уровне значимостипроверить нулевую гипотезуо равенстве неизвестной генеральной дисперсиигипотетическому (предполагаемому) значениюпри конкурирующей гипотезенеобходимо вычислить наблюдаемое значение критерия

где – исправленная выборочная дисперсия; n– объем выборки, и по таблице критических точек распределения(прил. 7) по заданному уровню значимостии числу степеней свободынайти критическую точкуЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2.При конкурирующей гипотезенаходят левуюи правуюкритические точки. Если– нет оснований отвергнуть нулевую гипотезу. Еслиили– нулевую гипотезу отвергают.

Сравнение двух средних генеральных совокупностей,

дисперсии которых известны

(большие независимые выборки)

Пусть n и m – объемы больших независимых выборок, по которым найдены соответствующие выборочные средниеиГенеральные дисперсииизвестны.

Правило 1. Чтобы при заданном уровне значимости проверить нулевую гипотезу о равенстве математических ожиданий (генеральных средних) двух нормальных генеральных совокупностей с известными дисперсиями (в случае больших выборок) при конкурирующей гипотезенеобходимо вычислить наблюдаемое значение критерия

и по таблице значений функции Лапласа (прил. 2) найти критическую точку из равенства

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе находят критическую точкупо таблице значений функции Лапласа (прил. 2.) из равенства

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе находятпо правилу 2. Если– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Сравнение двух средних нормальных генеральных

совокупностей, дисперсии которых неизвестны

и одинаковы (малые независимые выборки)

Пусть n,m– объемы малых независимых выборок– соответствующие выборочные средние;– исправленные выборочные дисперсии.

Правило 1.Чтобы при заданном уровне значимостипроверить нулевую гипотезуо равенстве математических ожиданий (генеральных средних) двух нормальныхсовокупностей с неизвестными, но одинаковыми дисперсиями (в случае малых независимых выборок) при конкурирующей гипотезенадо вычислить наблюдаемое значение критерия

и по таблице критических точек распределения Стьюдента (прил. 8), по заданному уровню значимостии числу степеней свободынайти критическую точку Если – нет оснований отвергнуть нулевую ги­потезу. Если– нулевую гипотезу отвергают.

Правило 2.При конкурирующей гипотезенаходят критическую точкупо таблице критических точек распределения Стьюдента (прил. 8), по уровню значимостии по числу степеней свободыЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 3.При конкурирующей гипотезенаходят сначала критическую точкупо правилу 2 и полагают,Если– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Сравнение выборочной средней с гипотетической

генеральной средней нормальной совокупности

Пусть дисперсия генеральной совокупности известна.

Правило 1.Чтобы при заданном уровне значимостипроверить нулевую гипотезуо равенстве генеральной среднейaнормальной совокупности с известной дисперсиейгипотетическому (предполагаемому) значениюпри конкурирующей гипотезенадо вычислить наблюдаемое значение критерия

и по таблице значений функции Лапласа (прил. 2) найти критическую точку двусторонней критической области из равенства

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2.При конкурирующей гипотезекритическую точку правосторонней критической области находят из равенства

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 3.При конкурирующей гипотезесначала находят вспомогательную критическую точку по правилу2, а затем полагают границу левосторонней критической области

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Мощность критерия проверки нулевой гипотезы о равенстве генеральной средней гипотетическому значениюпри известном среднем квадратическом отклонениинаходят в зависимости от вида конкурирующей гипотезы.

При конкурирующей гипотезе для гипотетического значения генеральной среднеймощность правостороннего критерия вычисляется по формуле:

где

При различных значениях функция мощности одностороннего критерия равна

При конкурирующей гипотезе для гипотетического значения генеральной среднеймощность двустороннего критерия равна

где находят из равенства

При различных значениях функция мощности двустороннего критерия равна

Здесь – функция Лапласа.

Если дисперсия генеральной совокупности неизвестна, то в качестве критерия проверки нулевой гипотезы принимают случайную величину

где 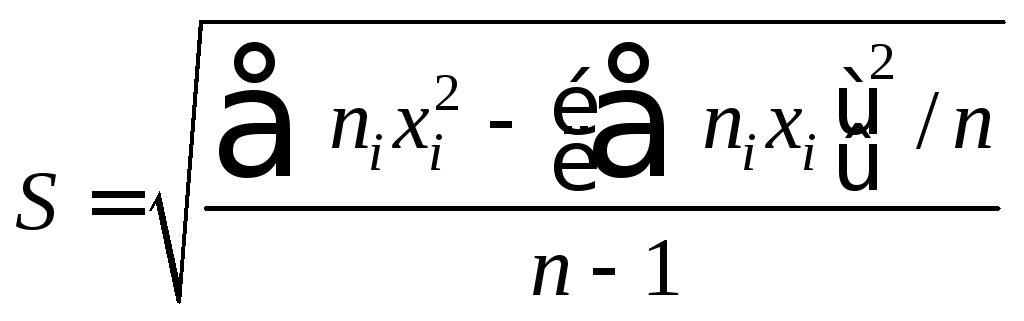– исправленное среднее квадратическое отклонение.

Величина Tимеет распределение Стьюдента сk = n – 1 степенями свободы.

Правило 1.Чтобы при заданном уровне значимостипроверить нулевую гипотезуH₀:a = a₀о равенстве неизвестной генеральной среднейa(нормальной совокупности с неизвестной дисперсией) гипотетическому значениюa₀при конкурирующей гипотезеH₁:a  a₀, необходимо вычислить наблюдаемое значение критерия

Далее по таблице критических точек распределения Стьюдента (прил. 8), по заданному уровню значимости , помещенному в верхней строке таблицы, и числу степеней свободыk = n – 1 найти критическую точку

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе по уровню значимости и числу степеней свободы k = n – 1находят критическую точку правосторонней критической области. Если– нет основания отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 3.При конкурирующей гипотезеH₁:a < a₀сначала находят вспомогательную критическую точку по правилу 2и полагают границу левосторонней критической областиЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Сравнение двух средних нормальных генеральных

совокупностей с неизвестными дисперсиями

(зависимые выборки)

Пусть генеральные совокупности XиYраспределены нормально, причем их дисперсии неизвестны. Из этих совокупностей извлечены зависимые выборки одинакового объемаn, варианты которых соответственно равныx_iиy_i. Вводятся обозначения:– разности вариант с одинаковыми номерами,– средняя разностей вариант с одинаковыми номерами,– исправленное среднее квадратическое отклонение.

Чтобы при заданном уровне значимости проверить нулевую гипотезуо равенстве двух средних нормальных совокупностейXиYс неизвестными дисперсиями (в случае зависимых выборок одинакового объема) при конкурирующей гипотезе:необходимо вычислить наблюдаемое значение критерия

и по таблице критических точек распределения Стьюдента (прил. 8), по заданному уровню значимости и числу степеней свободынайти критическую точкуЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Сравнение наблюдаемой относительной частоты

с гипотетической вероятностью появления события

Пусть по достаточно большому числу nнезависимых испытаний, в каждом из которых вероятностьpпоявления события постоянна, но неизвестна, найдена относительная частотаТребуется при заданном уровне значимостипроверить нулевую гипотезу, состоящую в том, что неизвестная вероятностьpравна гипотетической вероятности

Правило 1. Чтобы при заданном уровне значимостипроверить нулевую гипотезуо равенстве неизвестной вероятностиpгипотетической вероятностипри конкурирующей гипотезенадо вычислить наблюдаемое значение критерия

и по таблице функции Лапласа (прил. 2) найти критическую точку из равенства

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2.При конкурирующей гипотезенаходят критическую точку правосторонней критической области из равенства

Если – нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе находят сначала вспомогательную критическую точкупо правилу 2, а затем полагают границу левосторонней критической областиЕсли– нулевую гипотезу отвергают. Если– нет оснований отвергнуть нулевую гипотезу.

Сравнение двух вероятностей

биномиальных распределений

Пусть в двух генеральных совокупностях проводятся независимые испытания: в результате каждого испытания событие Aможет появиться в первой совокупности с неизвестной вероятностьюp₁, а во второй – с неизвестной вероятностьюp₂. По выборкам, извлеченным из первой и второй совокупностей, найдены соответствующие частоты:

где m₁,m₂– числа появления событияA;

n₁,n₂– количества испытаний.

В качестве оценок неизвестных вероятностей примем относительные частоты: Требуется при заданном уровне значимостипроверить нулевую гипотезу, состоящую в том, что вероятностиp₁иp₂равны между собой:Другими словами, требуется установить, значимо или незначимо различаются относительные частотыw₁иw₂.

Считается, что выборки имеют достаточно большой объем.

Правило 1. Для того чтобы при заданном уровне значимости  проверить нулевую гипотезу о равенстве ве­роятностей появления события в двух генеральных совокупно­стях (имеющих биномиальное распределение) при конкурирую­щей гипотезенадо вычислить наблюдаемое значение критерия

и по таблице функции Лапласа (прил. 2) найти критическую точку по равенствуЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 2.При конкурирующей гипотезенаходят критическую точку правосторонней критической области по равенствуЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Правило 3.При конкурирующей гипотезенаходят критическую точкупо правилу 2, а затем полагают границу левосторонней критической областиЕсли– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Пример 1. По двум независимым выборкам, объемы которых иизвлеченным из нормальных генеральных совокупностейX и Y, найдены исправленные выборочные дисперсии иПри уровне значимостипроверить нулевую гипотезуо равенстве генеральных дисперсий, при конкурирующей гипотезе

Решение. Найдем отношение большей исправленной дисперсии к меньшей:

По условию конкурирующая гипотеза имеет вид поэтому критическая область – правосторонняя.

По таблице критических точек распределения F Фишера–Снедекора (прил. 6), по уровню значимости и числам степеней свободыинайдем критическую точку

Так как то нет оснований отвергнуть гипотезу о равенстве генеральных дисперсий, т. е. выборочные исправленные дисперсии различаются незначительно.

Пример 2. По двум независимым выборкам, объемы которых иизвлеченным из нормальных генеральных совокупностей, найдены выборочные средние:иГенеральные дисперсии известны:Требуется при уровне значимости 0,01 проверить нулевую гипотезупри конкурирующей гипотезе

Решение. Найдем наблюдаемое значение критерия:

Конкурирующая гипотеза имеет вид поэтому критическая область – двусторонняя. Найдем правую критическую точку из равенства

По таблице значений функции Лапласа (прил. 2)

Так как то нулевую гипотезу отвергнем, т. е. выборочные средние различаются значимо.

Пример 3. По утверждению руководства фирмы, средний размер дебиторского счета равен 187,5 тыс. руб. Ревизор составляет случайную выборку из 10 счетов и обнаруживает, что средняя арифметическая выборки равна 175 тыс. руб. при среднем квадратическом отклонении 35 тыс. руб. Выяснить, может ли оказаться в действительности правильным объявленный размер дебиторского счета. Принять уровень значимости равным

Решение. Здесь  тыс. руб.,  тыс. руб., n = 10, Так как дисперсия неизвестна, то для проверки гипотезыH₀: воспользуемся распределением Стьюдента. Тогда

По таблице распределения Стьюдента (прил. 8) при найдемТак както гипотезуо среднем размере дебиторского счета примем на уровне доверия

Пример 4. Двумя приборами в одном и том же порядке измерены шесть деталей и получены следующие результаты измерений (в сотых долях миллиметра):

При уровне значимости 0,05 установить, значимо или незначимо различаются результаты измерений, при условии, что они распределены нормально.

Решение. Вычислив разности получим:

Найдем выборочную среднюю, учитывая, что

Вычислим исправленное среднее квадратическое отклонение учитывая, что

Определим наблюдаемое значение критерия:

По таблице критических точек распределения Стьюдента (прил. 8), по уровню значимости 0,05 и числу степеней свободы найдем критическую точку

Так как – нет оснований отвергнуть нулевую гипотезу. Таким образом, средние результаты измерений различаются незначимо.

Задания