31.7. Основные законы распределения

случайных величин

Биномиальное распределение.Пусть производитсяnнеза­висимых опытов. В каждом из них с одной и той же вероятно­стьюpможет наступать некоторое событиеA. Рассматривается случайная величинаХ– число наступлений событияAвnопы­тах. Тогда дискретная случайная величинаХможет принимать значения 0, 1, 2, …,nс вероятностями

Это распределение случайной величины Хназываетсябино­миальным. В этом случаегде

Распределение Пуассона. Говорят, что случайная величинаХраспределенапо закону Пуассона, если она принимает целые значения 0, 1, 2, … с вероятностями

соответственно, где – параметр распределения. При этом

Математическое ожидание и дисперсия случайной величи­ны, распределенной по закону Пуассона, равны между собой и равны параметру

Распределение Пуассона из всех дискретных распределений наиболее часто встречается в приложениях. Оно является предельным для биномиального распределения, если мы зафиксируем значение kи станем устремлять число опытовnк бесконечности, а вероятностьp– к нулю, притом так, чтобы их произведение оставалось равным постоянному числу Сэтим свойством распределения Пуассона – выражать биномиальное распределение при большом числе опытов и малой вероятности события – связано часто применяемое для него названиезакона редких явлений.

Геометрическое распределение.Дискретная случайная ве­личинаХимеет геометрическое распределение, если она принимает значенияk = 1, 2, 3, … (счетное множество значений) с вероятностями

соответственно, где

Математическое ожидание и дисперсия случайной величины, имеющей геометрическое распределение, соответственно определяются следующими формулами:

Гипергеометрическое распределение.Дискретная случай­ная величинаХимеетгипергеометрическое распределение, ес­ли она принимает значениеmс вероятностями

где

Математическое ожидание и дисперсия случайной величи­ны, имеющей гипергеометрическое распределение с параметра­ми n,M,N:

Равномерное распределение.Непрерывная случайная величинаХимеетравномерное распределение на отрезке[a;b], если ее плотность распределения вероятностейf(x) постоянна на отрезке, а вне его равна нулю:

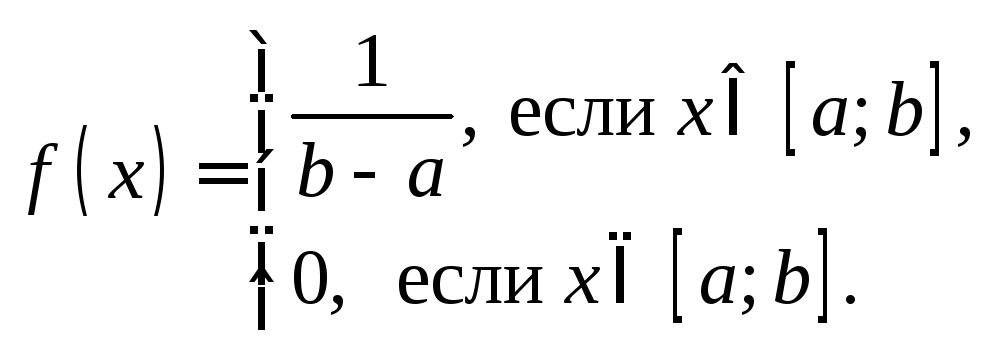
Функция распределения F(x) для равномерно распределенной случайной величиныХимеет вид

Числовые характеристики равномерного распределения:

Показательное (экспоненциальное) распределение.Непре­рывная случайная величинаХимеетпоказательное (экспонен­циальное) распределение, если плотность распределения вероятностей имеет вид

где – параметр данного распределения.

Функцию распределения случайной величины Х, распреде­ленную по показательному закону, находят по формуле

Математическое ожидание и дисперсия показательно рас­пределенной случайной величины Хопределяются равенствами:

Часто длительность времени безотказной работы определенного механизма имеет показательное распределение, функция распределения которого

определяет вероятность отказамеханизма за время длительностьюt, гдеt₀ = 0 – начальный момент времени,t – момент времени, когда происходит отказ,T – непрерывная случайная величина – длительность времени безотказной работы механиз­ма,– интенсивность отказов (среднее число отказов в единицу времени).

Функцией надежностиR(t) называют функцию, опреде­ляющую вероятность безотказной работы механизма за время длительностьюt:

Нормальное распределение.Непрерывная случайная вели­чинаХимеет нормальное распределение (говорят также, что она распределена по нормальному закону или по закону Гаусса), если ее плотность распределения вероятностей имеет вид

Параметры aипредставляют собой соответственно мате­матическое ожидание и среднее квадратичное отклонение слу­чайной величиныХ, т. е.

Отсюда

Если a = 0 и = 1, то соответствующее нормальное распре­деление называетсястандартным. Функция распределения для такой случайной величины имеет вид

и обладает (помимо обычных свойств функции распределения) свойством

В общем случае функция распределения нормального закона выражается формулой

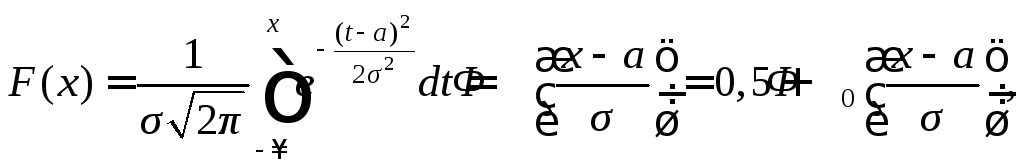
где 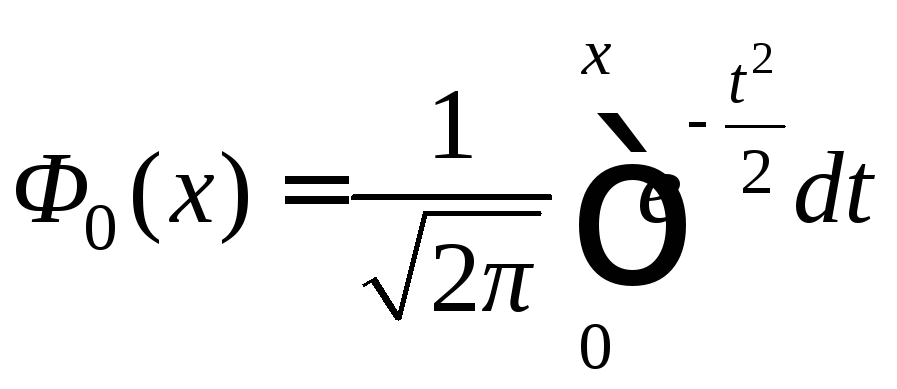–функция Лапласа.

Связь функции Ф(x) с функцией ЛапласаФ₀(x) выражается формулой

Вероятность попадания нормально распределенной случай­ной величины в заданный интервал (; ) определяется формулой

Вероятность попадания нормально распределенной случай­ной величины Хв интервалсимметричный отно­сительно центра рассеянияa, находится по формуле

В частности, т. е. нормально распределенная случайная величинаХотклоняется от своего математического ожиданияa, как правило, менее чем на 3. Это утверждение называется «правилом трех сигм».

Пример 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2; 8).

Решение. Имеем:

Пример 2. Длительность времени безотказной работы элемента имеет показательное распределение

Найти вероятность того, что за время длительностью t = 50 ч:

1) элемент откажет; 2) элемент не откажет.

Решение. 1) Поскольку функция распределения определяет вероятность отказа элемента за время длительностьюt, то, подставив t = 50 в формулу функции распределения, получим вероят­ность отказа:

2) Так как события «элемент откажет» и «элемент не откажет» яв­ляются противоположными, то вероятность того, что элемент не отка­жет равна

Заметим, что этот результат можно получить непосредственно, пользуясь функцией надежности которая определяет веро­ятность безотказной работы элемента за время длительностьюt:

Пример 3. Определить вид закона распределения случайной вели­чины X, если ее плотность вероятностей имеет вид Найти: 1)M(X); 2) (X); 3) значение коэффициента A; 4)

Решение. Произведем преобразования

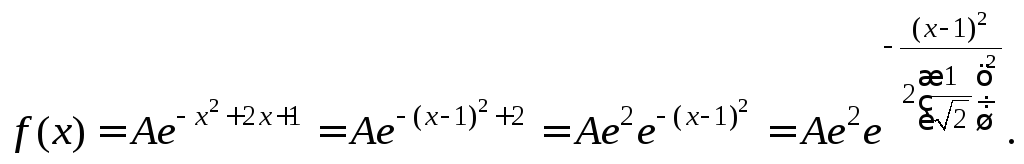
Сравнивая данную функцию с плотностью

нормального распределения, делаем вывод, что случайная величина Х имеет нормальное распределение.

1) Очевидно, M(X) = 1.

2)

3) Найдем значение коэффициента F из равенства

где откуда

Таким образом, плотность вероятностей случайной величины Х имеет вид

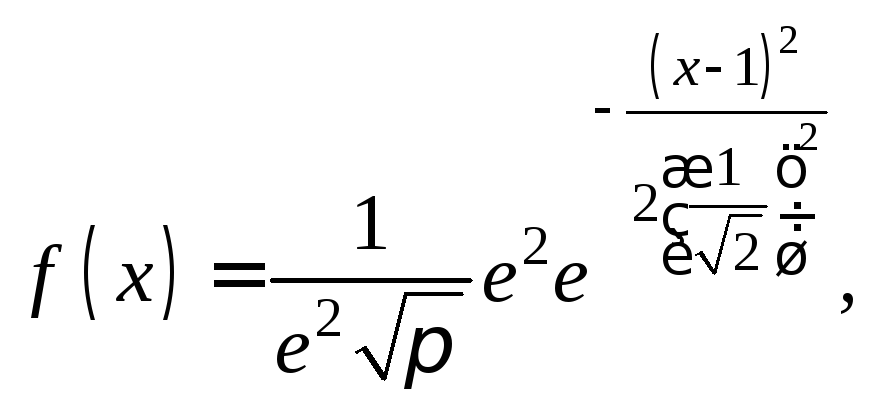т. е.

4) Используя формулу

найдем, что

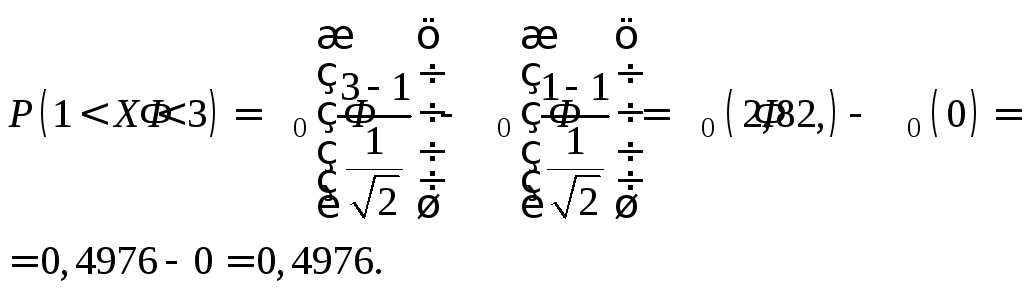
Значение Ф₀(2,82) найдено по таблице значений функции Лапласа (прил. 2)

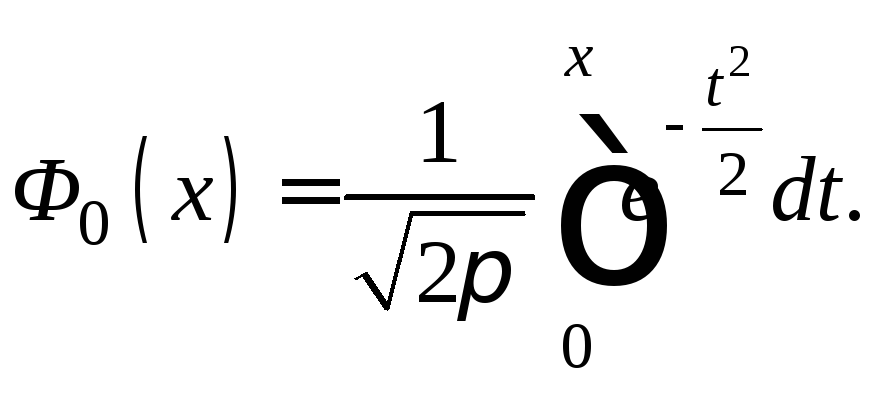
Задания