33. Вычислительная математика

33.1. Элементы теории погрешностей

Приближенное значение некоторой величины называется приближенным числом, а истинное значение величины – точным числом. Мерой точности приближенных чисел является погрешность. Существуют три вида погрешностей: 1) неустранимая погрешность; 2) погрешность метода; 3) вычислительная погрешность.

Основная задача теории погрешностей - нахождение области неопределенности результата.

Если A - точное число, a - его приближенное значение, то пишут

Число a называется приближенным значением (или приближением) числа A с точностью до если выполняется неравенство

Величина называетсяабсолютной погрешностью приближенного числа a (иногда употребляется термин «предельная абсолютная погрешность»). Значение точного числа A записывают в виде а приближенного числаa - в виде

Относительной погрешностью приближенного числа a называется величинаудовлетворяющая условию

(33.1)

В частности, можно принять

(33.2)

Относительная погрешность часто выражается в процентах.

Абсолютная погрешность отражает количественную сторону погрешности, а относительная погрешность - качественную.

Всякое десятичное число a , точное и приближенное, может быть представлено в виде

(33.3)

где - цифры числа a, причем

Все сохраняемые десятичные знаки называются значащими цифрами приближенного числа a. Форма записи приближенного числа a в виде (33.3), т. е.

где g - множитель, состоящий только из значащих цифр (кроме нуля целых), называется нормализованной.

Значащая цифра приближенного числа (33.3) называетсяверной в узком смысле, если иверной в широком смысле, если Значащие цифры, не являющиеся верными, называютсясомнительными.

Если цифра приближенного числаa является верной в узком смысле, то за относительную погрешность можно принять если цифра– верная в широком смысле, то –

Округление чисел

При округлении десятичной дроби сохраняют одну или несколько ее цифр, считая слева направо, и отбрасывают все последующие, или (если это необходимо для сохранения разрядов) отбрасываемые цифры заменяют нулями. Существуют три способа округления чисел.

1. Округление по правилу дополнения (или просто округление) осуществляется по следующему правилу: если первая слева из отбрасываемых цифр числа больше или равна пяти, то последняя сохраняемая цифра числа усиливается (увеличивается на единицу), в противном случае эта цифра остается без изменения.

2. При округлении с недостатком последняя сохраняемая цифра числа остается без изменения.

3. При округлении с избытком последняя сохраняемая цифра числа усиливается. В этом случае будем писать:

При округлении приближенного числа получаем новое приближенное числос абсолютной погрешностью где величина удовлетворяет неравенству

Погрешности арифметических действий

Имеют место следующие формулы:

(33.4)

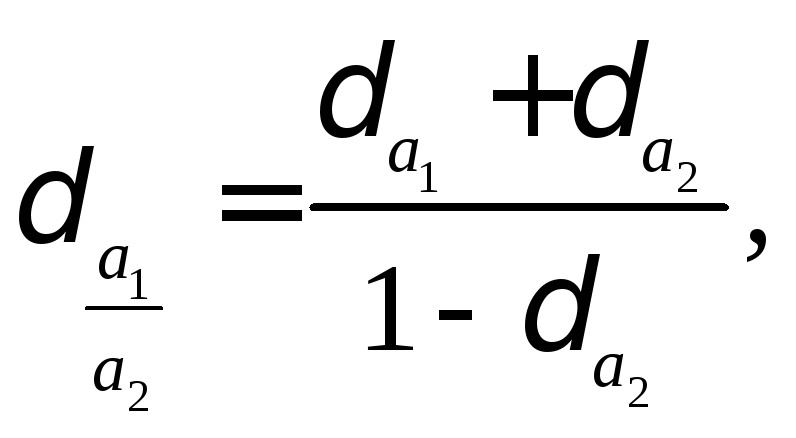где

Считая относительные погрешности достаточно малыми, можно использовать приближенные формулы:

(33.5)

(33.6)

При сложении и вычитании чисел, имеющих разное количество десятичных знаков, необходимо:

1) выделить число с наименьшим количеством десятичных знаков;

2) остальные числа округлить, сохранив в них на один знак больше, чем у выделенного числа;

3) полученный результат округлить на один знак.

При умножении и делении чисел, имеющих разное количество значащих цифр, необходимо:

1) выделить число с наименьшим количеством значащих цифр;

2) остальные числа округлить, сохранив в них на одну значащую цифру больше, чем у выделенного числа;

3) в результате сохранить столько значащих цифр, сколько их было у выделенного числа.

Пример 1. Определить, какое равенство точнее: или

Решение. Обозначим Согласно формуле (33.1), имеем

Так как то равенствоявляется более точным.

Пример 2. Округлить сомнительные цифры приближенного числа оставив верные цифры в широком смысле, если Определить абсолютную погрешность результата.

Решение. Представим в видеи из формулы (33.2), найдем

т. е.

Так как то в числе верными в широком смысле являются три цифры: 8, 2, 6. Округляем число a до трех значащих цифр: Тогда

Поскольку то числоимеет две верные в широком смысле цифры: 8, 2. Поэтому округляем числоa до двух значащих цифр: Тогда

т. е.

Так как то две оставшиеся цифры результатаверны в широком (и в узком!) смысле. Таким образом,

Пример 3. Определить, с каким минимальным количеством верных значащих цифр в узком смысле надо взять число e, чтобы относительная погрешность при этом не превышала

Решение. В соответствии с условием т. е.ИмеемотсюдаиСледовательно,

Пример 4. Вычислить значение выражения и определить погрешности результата, если и у каждого из заданных чисел все выписанные цифры верные в узком смысле.

Решение. Находим

Вычисляем погрешности, используя формулы (33.4)–(33.6):

В окончательном результате следует оставить три значащие цифры, так как столько их имеет приближенное данное с наименьшим количеством значащих цифр:

т. е. Следовательно,

т. е.

Задания