I уровень

1.1. Определите, сколько действительных корней имеет уравнение:

1) 2)

3) 4)

1.2. Отделите графически корни уравнения:

1) 2)

1.3. Отделите аналитически корни уравнения:

1) 2)

1.4. Отделите корни уравнения указав отрезки длины 0,1.

1.5. Найдите действительные корни уравнения методом половинного деления.

1.6. Решите уравнение с помощью метода хорд:

1) 2)

1.7. Решите уравнение методом Ньютона:

1) 2)

1.8. Найдите все действительные корни уравнения:

1) 2)

II уровень

2.1. Найдите действительные корни уравнения при методом половинного деления с точностью до

2.2. Найдите методом хорд с точностью до действительные корни уравнения:

1) 2)

2.3. Используя метод Ньютона, найдите с точностью до действительные корни уравнения:

1) 2)

2.4. Комбинированным методом хорд и касательных найдите с точностью до действительные корни уравнения

III уровень

3.1. Докажите, что уравнение имеет три простых действительных корня тогда и только тогда, когда коэффициентыp и q удовлетворяют неравенству

3.2. Приближенным значением корня уравнения являетсяОпределите абсолютную погрешность этого значения.

3.3. Найдите наименьший положительный корень уравнения с точностью до

3.4. Найдите где с тремя верными значащими цифрами в узком смысле.

3.5. Составьте алгоритмическую схему приближенного решения уравнения с заданной точностью методом половинного деления.

3.6. Составьте алгоритмическую схему приближенного решения уравнения с заданной точностью методом хорд.

3.7. Составьте алгоритмическую схему приближенного решения уравнения с заданной точностью методом Ньютона.

3.8. Составьте алгоритмическую схему приближенного решения уравнения с заданной точностью комбинированным методом хорд и касательных.

33.4. Приближенное вычисление интегралов

Пусть требуется вычислить определенный интеграл

Интегрирование с помощью рядов

Предположим, что подынтегральная функция разлагается в степенной ряд

(33.19)

сходящийся в интервале который содержит отрезок интегрирования Тогда искомый интеграл I можно представить в виде числового ряда

(33.20)

Используем непрерывную аппроксимацию для функции и в качестве аппроксимирующей функции возьмем n-ю частичную сумму ряда (33.19):

Если ряд (33.20) знакочередующийся, то для оценки его остаточного члена можно воспользоваться известным следствием признака Лейбница. В случае знакопостоянного ряда (33.20) обычно применяется мажорирование бесконечно убывающей геометрической прогрессией.

Численное интегрирование

Задача численного интегрирования заключается в вычислении значения определенного интеграла I на основании ряда значений подынтегральной функции в точках промежутка интегрирования. Формулы численного интегрирования называются квадратурными формулами. Рассмотрим простейшие из них, использующие локальную интерполяцию при точечной аппроксимации подынтегральной функции.

С помощью точек разобьем отрезок интегрирования на n равных частичных отрезков с шагом интегрирования и обозначим Величина где– численное значение выбранной квадратурной формулы, называетсяостаточным членом квадратурной формулы.

Формула левых прямоугольников:

Формула правых прямоугольников:

Если непрерывна на то для формул левых и правых прямоугольников выполняется

Формула средних прямоугольников:

(33.21)

Если непрерывна на то для формулы средних прямоугольников выполняется

(33.22)

Формула трапеций:

(33.23)

Если непрерывна на то для формулы трапеций выполняется

(33.24)

Формула Симпсона (формула парабол):

(33.25)

где

Если непрерывна на то для формулы Симпсона выполняется

(33.26)

Пример 1. Вычислить интеграл с точностью до путем разложения подынтегральной функции в степенной ряд.

Решение. Воспользуемся формулой Маклорена

Заменяя в ней x на получим ряд

Этот ряд сходится при любом поэтому его можно почленно интегрировать. Тогда

Полученный числовой ряд является знакочередующимся. Так как ното отсюда имеем оценку остаточного члена:

Поэтому для обеспечения заданной степени точности достаточно взять два члена ряда

Следовательно,

Пример 2. Вычислить интеграл разлагая подынтегральную функцию в степенной ряд и используя три члена этого разложения. Определить абсолютную погрешность результата.

Решение. Воспользуемся формулой

Получим

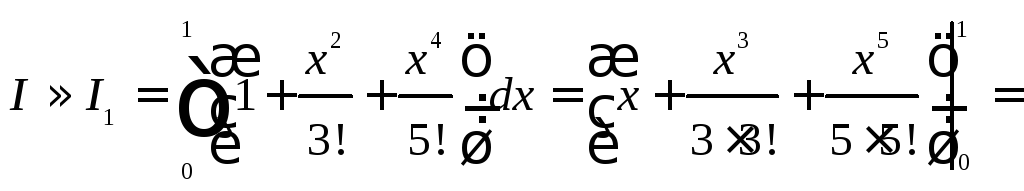
Найдем абсолютную погрешность

т. е. В окончательном результате оставим шесть значащих цифр: Тогда

т. е. Следовательно,

Пример 3. Вычислить с помощью формулы средних прямоугольников интеграл принявОпределить абсолютную погрешность результата.

Решение. По заданным пределам интегрирования инайдем шагВ данном случае точками разбиения отрезкабудутиТогда по формуле (33.21), гдеполучим

Находим абсолютную погрешность метода Так как

то, используя формулу (33.22), имеем

т. е. В окончательном результате оставим четыре значащие цифры: Тогда

т. е. Следовательно,

Для сравнения приведем точное значение интеграла:

Пример 4. Вычислить с помощью формулы трапеций интеграл с точностью до

Решение. Для определения необходимого числа разбиений n оценим остаточный член по формуле (33.24). Так как

то

Решая неравенство

получим примем

Зная пределы интегрирования, найдем шаг Точками разбиения служатНайдем соответствующие значения подынтегральной функцииТогда по формуле (33.23) получаем

Следовательно,

Для сравнения приведем точное значение интеграла:

Пример 5. Вычислить с помощью формулы Симпсона интеграл с точностью до

Решение. Для определения n оценим остаточный член по формуле (33.26). Можно показать (проверить самостоятельно!), что

Поэтому

Решая неравенство

получим примем

Нужно определить значения подынтегральной функции при для следующих значений аргумента: Найдем соответствующие значения Тогда по формуле (33.25) получим

Следовательно,

Задания