31.8. Функция одного случайного аргумента

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то эта случайная величина называется функцией случайного аргу­мента (случайной величины) Х. В этом случае пишут:

Если Х – дискретная случайная величина и функция монотонна, то возможные значенияY находят из равенства

где x_i– возможные значения случайной величиныХ.

Вероятности возможных значений случайной величины Yнаходят из равенства

Если – немонотонная функция, то различным зна­чениям случайной величиныХмогут соответствовать одинако­вые значения случайной величиныY. В этом случае вероятность повторяющегося значения случайной величиныYравна сумме вероятностей тех возможных значенийХ, при которых случай­ная величинаYпринимает одно и то же значение.

Математическое ожидание и дисперсия случайной величи­ны Yопределяются соответственно равенствами

и

,

где

Если Х– непрерывная случайная величина с плотностью распределенияf(x) и если– дифференцируемая строго возрастающая или строго убывающая функция, то плотность распределенияg(y) случайной величинывыражается формулой

где – функция, обратная функции

Если же функциянемонотонная в промежутке воз­можных значенийХ, то весь указанный промежуток разбивается на n промежутков монотонности и обратная функция нахо­дится на каждом из них. Плотность распределенияслучай­ной величиныопределяется в этом случае по формуле

Для нахождения математического ожидания и дисперсии слу­чайной величины можно воспользоваться формулами

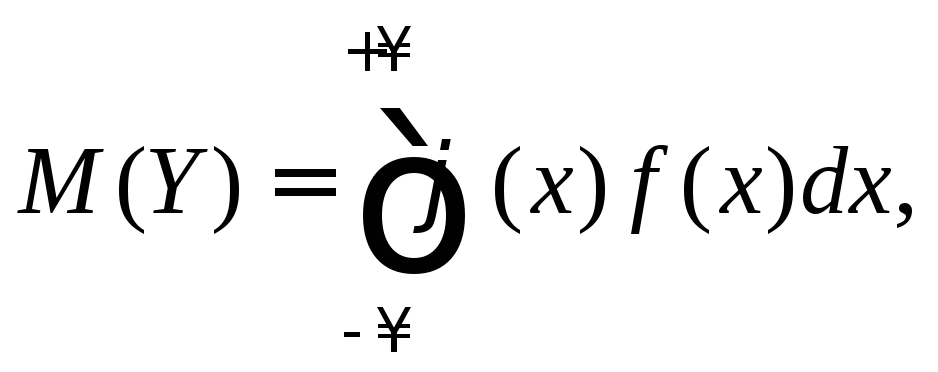
Пример 1. Пусть закон распределения случайной величины Х имеет вид:

Х	–2	–1	0	1	2	3
P	0,1	0,2	0,4	0,02	0,15	0,13

Найти закон распределения величины

Решение. Возможные значения случайной величины Y это (–2)², (–1)², 0², 1², 2², 3², т. е. 0, 1, 4, 9. Их вероятности:

Таким образом, закон распределения случайной величины Y будет:

Y	0	1	4	9
P	0,4	0,22	0,25	0,13

Пример 2. Случайная величина Х равномерно распределена в интервале (–1; 1). Найти плотность вероятностей случайной величины Y = 3X.

Решение. Найдем плотность распределения f(x) случайной величи­ны Х. Величина Х равномерно распределена в интервале (–1; 1), поэто­му в этом интервале имеем

вне рассматриваемого интервала – f(x) = 0.

Так как функция y = 3x дифференцируема и строго возрастает, то применима формула

где – функция, обратная функцииy = 3x.

Найдем

Найдем

Найдем производную

Очевидно, что

Таким образом, Так какy = 3x, причем тоСледовательно, в интервале (–3; 3) искомая плотность распределениявне этого интервала

Контроль:

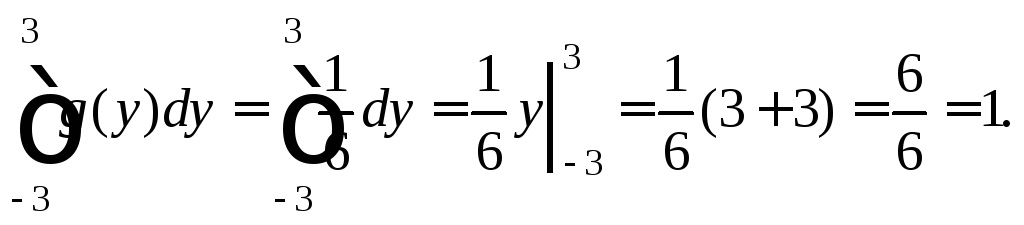
Задания

I уровень

1.1.Дискретная случайная величинаХзадана законом распределения:

Х	1	2	3	4	5
P	0,2	0,3	0,15	0,2	0,15

Запишите закон распределения случайной величины

1.2.Дискретная случайная величинаХзадана законом распределения:

Х	–2	–1	0	1	2	3
P	0,4	0,05	0,1	0,05	0,3	0,1

Найдите закон распределения случайной величины

1.3.Дискретная случайная величинаХзадана законом распределения:

Х
P	0,3	0,2	0,4	0,1

Найдите закон распределения случайной величины

1.4.Дискретная случайная величинаХзадана рядом распределения:

Х	–2	–1	0	1	2	3	4
P	0,15	0,05	0,35	0,20	0,05	0,10	0,10

Найдите:

1) распределение случайной величины

2) математическое ожидание и дисперсию случайной величины Y.

1.5.Задана плотность распределенияf(x) случайной величиныХ, возможные значения которой заключены в интервале (a; b). Найдите плотность распределения случайной величины

1.6. Задана плотность распределения f(x) случайной величины Х, возможные значения которой заключены в интервале (a;b). Найдите плотность распределенияg(y) случайной величиныY, если:

1) 2)

1.7.Дискретная случайная величинаХимеет ряд распределения:

Х	–1	0	1	2	3	4
P	0,4	0,10	0,10	0,20	0,05	0,15

Найдите математическое ожидание и дисперсию случайной величины

1.8.Непрерывная случайная величинаХраспределена в интервале (0; 1) с плотностью

Найдите математическое ожидание и дисперсию случайной величины