
- •И. Л. Кирина, д. С. Герасимов, а. С. Ставышенко
- •Оглавление
- •Введение
- •Глава 1. Теоретическиеосновы исследования экономикии управлениякачеством
- •1.1. Дефиниции понятия «качество»
- •1.1.1. Качество как экономическая категория
- •1.1.2. Количественная оценка показателей качества
- •1.1.3. Статистические методы и инструменты оценки качества
- •Определяющих качество продукции:
- •Основных дефектов деталей, вызывающих брак
- •1.2. Системный и процессный подходы к управлению качеством
- •1.2.1. Общие понятия
- •1.2.2. Отечественный опыт по разработке и применению систем
- •Система бездефектного изготовления продукции
- •Система бездефектного труда
- •Система качество, надежность, ресурс с первых изделий
- •Система научной организации труда по увеличению моторесурса
- •Комплексные системы управления качеством продукции
- •Комплексная система управления качеством продукции и эффективного использования ресурсов
- •1.2.3. Зарубежный опыт по разработке и применению систем
- •1.2.3.1. Зарубежные модели систем качества
- •1.2.3.2. Всеобщее управление качеством - tqm
- •Часть 1 касается «мягких», а часть 2 –«жестких» элементов tqm. Определение менеджмента всеобщего качества
- •Удовлетворение технических требований
- •Модель всеобщего руководства качеством
- •Элементы модели tqm
- •1.2.3.3. Системы менеджмента качества по модели исо9001
- •Системы менеджмента качества по модели исо9001
- •Использование принципов менеджмента качества
- •Основанная на процессном подходе
- •Модель совершенствования, разработанная Европейским фондом управления качеством (efqm ExcellenceModel)
- •Структура модели совершенствования efqm
- •Вопросы для обсуждения:
- •Глава 2. Экономическое обеспечение качества
- •2.1. Классификация затрат на качество
- •Новой и усовершенствованной продукции
- •2.2. Методы анализа затрат на качество
- •Вопросы для обсуждения:
- •Глава 3. Стандартизация как инструмент повышения качества и её экономическая эффективность
- •3.1. Стандартизация в системе экономики качества
- •3.2. Методы расчета экономической эффективности
- •Прогнозирование себестоимости методом удельных показателей
- •Прогнозирование себестоимости методом балльных оценок
- •Определение уровня себестоимости изделия методом экспоненциального сглаживания
- •Методы расчета экономической эффективности стандартизации продукции
- •Стадия проектирования
- •Стадия изготовления
- •Экономическая эффективность повышения надежности
- •Экономическая эффективность повышения производительности
- •3.3. Прочие источники экономической эффективности
- •3.4. Особенности расчета экономической эффективности
- •3.5. Особенности расчета экономической эффективности
- •3.6. Экономическая эффективность общетехнических
- •Единая система конструкторской документации (ескд)
- •Единые системы технологической документации (естд)
- •Система автоматизированного проектирования (сапр)
- •Единая система технологической подготовки производства (естпп)
- •Единая система допусков и посадок.
- •Система стандартов безопасности труда (ссбт)
- •Система стандартов в области охраны природы и улучшения использования природных ресурсов
- •3.7. Экономическая эффективность международной стандартизации
- •3.8. Порядок и методика проведения экономической экспертизы
- •Пример расчета экономической эффективности внедрения государственного стандарта «Машины для внесения минеральных удобрений. Общие технические требования»
- •Пример расчета экономической эффективности разработки и внедрения пкс «Средства электротермометрии»
- •Вопросы для обсуждения:
- •Глава 4. Управление качеством средствами стандартизации
- •4.1. Координация и планирование работ по стандартизации
- •4.2. Нормирование работ по стандартизации
- •4.2.1. Основные принципы построения нормативно-справочной базы
- •4.2.2. Действующие методы определения трудоемкости, затрат
- •Метод определения затрат на основе фактических затрат на разработку стандарта минимальной сложности
- •Метод определения затрат на основе фактических расходов на разработку аналогичного стандарта
- •Метод определения затрат на основе фактической трудоемкости аналогичного стандарта
- •Метод определения затрат на основе среднегодовых затрат на одного среднесписочного работника
- •Методика нормирования продолжительности и затрат на разработку стандартов
- •Сетевое планирование и управление
- •Параметры сетевой модели
- •Резерв времени путей и работ
- •Зависимый резерв времени работы r3(I,j)
- •Независимый резерв времени работы Rн(I,j)
- •Свободный резерв времени работы (Rcij)
- •Анализ и оптимизация сетевой модели
- •Графический метод оптимизации сетевой модели — "время-затраты"
- •Перечень документов
- •Перечень документов
- •Методика определения затрат на проведение экспертизы проектов стандартов и технических условий в системе Росстандарта России
- •Методика определения затрат на внедрение стандартов
- •Действующие нормативы эффективности применения стандартных решений
- •Пример расчета экономической эффективности внедрения результатов стандартизации по сапр
- •Пример расчета затрат на экспертизу1
- •Пример расчета экономической эффективности внедрения результатов стандартизации по сапр
- •Вопросы для обсуждения
- •Глоссарий
- •Список литературы
- •Экономика качества
Зависимый резерв времени работы r3(I,j)
Поскольку резерв времени пути Liможет быть использован для увеличения цикла работ, находящихся на этом пути, можно сказать, что любая из работ пути Liна его участке, не совпадающем с критическим путем, обладает резервом времени. Но у этого резерва есть особенность: если мы его используем частично или целиком для увеличения цикла t(i,j) какой-либо работы (i,j), то соответственно уменьшается резерв времени у остальных работ Li. Поэтому такой резерв времени пути, на котором она находится, называется зависимым резервом времени работы (i,j) и обозначается через R3(i,j).
Независимый резерв времени работы Rн(I,j)
У отдельных работ помимо зависимого резерва времени может иметься и независимый резерв времени, обозначаемый черезRн(i,j). Он образуется в том случае, когда циклы работ (i,j) меньше, чем разность между наиболее ранним из возможных сроков свершения непосредственно следующего за данной работой события j и наиболее поздним из допустимых сроков свершения непосредственно предшествующего ей события i:
Rн(i,j)=Тp(j) —Tп(i)—t(ij). (4.14)
Свободный резерв времени работы (Rcij)
Свободный резерв времени работы (Rcij) — это разность между ранними сроками наступления событий i и j за вычетом продолжительности работы t(i,j):
Rcij=Тpj—Tpi—tij. (4.15)
Свободный резерв времени работы — максимальный период времени, на который можно увеличить продолжительность или отсрочить ее начало, не изменяя при этом ранних сроков последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок.
Возможности смещения сроков начала и окончания каждой работы определяется с помощью ранних и поздних сроков наступления событий, между которыми выполняется данная работа:
ранний срок начала работы Tрнij=Tpi;
поздний срок начала работы Тnнij=Тnj—tij;
ранний срок окончания работы Троij=Трj+tij;
поздний срок окончания работы Тnоij=Тnj.
Анализ и оптимизация сетевой модели
Первоначально разработанная сетевая модель обычно не является лучшей по срокам выполнения работ и использования ресурсов. Поэтому исходная сетевая модель подвергается анализу и оптимизации по одному из ее параметров.
Анализ позволяет оценить целесообразность структуры модели, определить степень сложности выполнения каждой работы, загрузку исполнителей работ на всех этапах выполнения комплекса работ.
Относительная сложность соблюдения сроков выполнения работ на некритических путях характеризуется коэффициентом напряженности работКн(i,j):
 (4.16)
(4.16)
где
 —
продолжительность максимального пути,
проходящего через данную работу;
—
продолжительность максимального пути,
проходящего через данную работу;
 —продолжительность
отрезка этого пути, совпадающего с
критическим путем;
—продолжительность
отрезка этого пути, совпадающего с
критическим путем;
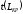 —продолжительность
критического пути.
—продолжительность
критического пути.
Чем больше коэффициент напряженности, тем сложнее выполнить работы в установленные сроки.
Используя понятие "резерва времени пути", Кн(i,j) можно определить следующим образом:
 .
(4.17)
.
(4.17)
При этом необходимо иметь в виду, что резерв времени R(Li) пути Li может быть распределен между отдельными работами, находящимися на указанном пути, только в пределах зависимых резервов времени этих работ.
Величина коэффициента напряженности у разных работ в сети лежит в пределах 0<Кн(i,j) <1.
Для всех работ критического пути Кн(i,j) равен единице. Величина коэффициента напряженности помогает при установлении плановых сроков выполнения работ оценить, насколько свободно можно располагать имеющимися резервами времени. Этот коэффициент дает исполнителям работ представление о степени срочности работ и позволяет определить очередность их выполнения, если они не определяются технологическими связями работ.
Для анализа сетевой модели используется коэффициент свободы Кс(i,j), который показывает степень свободы или независимости циклов работ, имеющих свободный резерв времени, а также показывает, во сколько раз можно увеличить длительность работы t(i, j), не влияя на сроки свершения всех событий и остальных работ сети:
 (4.18)
(4.18)
При этом Кс(i,j) > 1 всегда. Если Кс(i,j) < 1, то это указывает на отсутствие независимого резервного времени у работы (i,j).
Оптимизация сетевых моделей по одному из ее параметров может быть осуществлена графическим или аналитическим методом. Решая задачу оптимизации сетевой модели, обычно рассчитывают минимальную продолжительность выполнения комплекса работ при ограничениях на используемые ресурсы.
Оптимизация сетевой модели, осуществляемая аналитическим методом, заключается в том, что в ее основу положена та закономерность, при которой время выполнения любой работы (t) прямо пропорционально ее объему (Q) и обратно пропорционально числу исполнителей (m), занятых на данной работе:
 (4.19)
(4.19)
Время,
необходимое для выполнения всего
комплекса работ
 определяется как сумма длительностей
составляющих работ:
определяется как сумма длительностей
составляющих работ:
 (4.20)
(4.20)
Однако рассчитанное таким образом общее время не будет минимальным, даже если количество исполнителей соответствует трудоемкости этапов.
Минимальное время для комплекса последовательно выполняемых работ и других разновидностей фрагментов сетевых моделей можно найти методом условно-эквивалентной трудоемкости.
Под условно-эквивалентной трудоемкостью понимают такую величину затрат труда, при которой численность исполнителей эквивалентной специальности распределяется между составляющими работами, обеспечивает наименьшее время их исполнения.
Условно-эквивалентная трудоемкость определяется по формуле:
 (4.21)
(4.21)
где
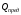 ,
, —
трудоемкости предшествующей и последующей
работ.
—
трудоемкости предшествующей и последующей
работ.
Минимальное время выполнения работ будет обеспечено при следующем распределении работающих по этапам:

 (4.22)
(4.22)
где m0 — общее количество работающих на определенных этапах.
