298 |
|
|
7 Gravitational Waves and the Binary Pulsars |
||
so that we conclude with the identifications |
|
|
|||
A = |
G |
; |
Kij = |
∂3Qij |
(7.3.93) |
36π |
∂t3 |
||||
and with the celebrated Einstein formula:
dE = G ∂3Qij 2
dt 45c5 ∂t3
(7.3.94)
expressing the energy radiated per unit time in terms of the square of the third derivative of the quadrupole moment.6
7.4 Quadruple Radiation from the Binary Pulsar System
Having retrieved Einstein 1918 formula for the emission power of quadrupole radiation, we consider now the analysis of a two-body system like that of the binary pulsar PRS1913+16 discovered by Hulse and Taylor (see Fig. 7.12). Our goal is that of computing the variable quadrupole moment of such a system in order to insert the result into the Einstein formula and obtain predictions about the energy loss through gravitational wave emission. Clearly such energy loss will result into a shrinking of the system and of its revolution period. The rate of that shrinking turns out to be a measurable quantity which can be compared with theoretical predictions thus providing very stringent tests on General Relativity. Our discussion follows closely and updates the treatment of the same problem presented in the book [8].
7.4.1 Keplerian Parameters of a Binary Star System
We begin with a Keplerian-Newton description of the orbit which will be corrected by General Relativity effects like the periastron advance.
From the viewpoint of Newtonian mechanics a two-body system can be reduced to a one-body problem in the case of central forces. For a potential:
V (r12) = − |
k |
(7.4.1) |
||
|
|
|||
r12 |
||||
introducing the reduced mass: |
|
|
|
|
μ = |
μ1μ2 |
(7.4.2) |
||
|
|
|||
μ1 + μ2 |
||||
6Note in the final formula (7.3.94) the appearance of the factor c5 in the denominator. The speed of light has been reinstalled at the appropriate power on the basis of dimensional analysis. In the previous steps of the calculation we always used natural units in which c = 1, namely our time variable was actually t ct .
7.4 Quadruple Radiation from the Binary Pulsar System |
299 |
Fig. 7.12 Schema of the binary pulsar system PRS1913+16 discovered by Russell Hulse and Joseph Taylor in 1974. For this discovery they received the Nobel Prize 1993
and naming r = r12, the solution of the dynamical problem is given by the elliptic orbits:
r |
= |
a(1 − e2) |
(7.4.3) |
||
|
|||||
|
1 |
+ |
e cos θ |
|
|
|
|
|
|||
where the geometrical parameters are related to the mechanical integral of motion, namely the energy and the angular momentum by:
a = − |
k |
; |
e2 = 1 + |
2El2 |
(7.4.4) |
2E |
μk2 |
In the case of the Newtonian potential:
|
|
|
|
k = Gμ1μ2 |
|
(7.4.5) |
||||
and therefore |
|
|
|
|
|
|
|
|
|
|
a |
= − |
μ1μ2G |
; |
e2 |
= |
1 |
+ |
2El2(μ1 + μ2) |
(7.4.6) |
|
2E |
μ13μ23G2 |
|||||||||
|
|
|
|
|||||||
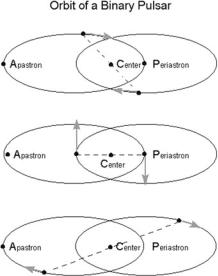
Hence if we deduce the geometrical parameters of a binary star system orbit, we can calculate the physical parameters (masses and angular momentum). How do we deduce the geometrical parameters? Help comes from the periastron advance that, in the case of the binary pulsar, can be measured notwithstanding the enormous distance of the system from the Earth (see Fig. 7.13).
