
- •Preface
- •Acknowledgements
- •Contents
- •1.1 Introduction
- •1.2 Classical Physics Between the End of the XIX and the Dawn of the XX Century
- •1.2.1 Maxwell Equations
- •1.2.2 Luminiferous Aether and the Michelson Morley Experiment
- •1.2.3 Maxwell Equations and Lorentz Transformations
- •1.3 The Principle of Special Relativity
- •1.3.1 Minkowski Space
- •1.4 Mathematical Definition of the Lorentz Group
- •1.4.1 The Lorentz Lie Algebra and Its Generators
- •1.4.2 Retrieving Special Lorentz Transformations
- •1.5 Representations of the Lorentz Group
- •1.5.1 The Fundamental Spinor Representation
- •1.6 Lorentz Covariant Field Theories and the Little Group
- •1.8 Criticism of Special Relativity: Opening the Road to General Relativity
- •References
- •2.1 Introduction
- •2.2 Differentiable Manifolds
- •2.2.1 Homeomorphisms and the Definition of Manifolds
- •2.2.2 Functions on Manifolds
- •2.2.3 Germs of Smooth Functions
- •2.3 Tangent and Cotangent Spaces
- •2.4 Fibre Bundles
- •2.5 Tangent and Cotangent Bundles
- •2.5.1 Sections of a Bundle
- •2.5.2 The Lie Algebra of Vector Fields
- •2.5.3 The Cotangent Bundle and Differential Forms
- •2.5.4 Differential k-Forms
- •2.5.4.1 Exterior Forms
- •2.5.4.2 Exterior Differential Forms
- •2.6 Homotopy, Homology and Cohomology
- •2.6.1 Homotopy
- •2.6.2 Homology
- •2.6.3 Homology and Cohomology Groups: General Construction
- •2.6.4 Relation Between Homotopy and Homology
- •References
- •3.1 Introduction
- •3.2 A Historical Outline
- •3.2.1 Gauss Introduces Intrinsic Geometry and Curvilinear Coordinates
- •3.2.3 Parallel Transport and Connections
- •3.2.4 The Metric Connection and Tensor Calculus from Christoffel to Einstein, via Ricci and Levi Civita
- •3.2.5 Mobiles Frames from Frenet and Serret to Cartan
- •3.3 Connections on Principal Bundles: The Mathematical Definition
- •3.3.1 Mathematical Preliminaries on Lie Groups
- •3.3.1.1 Left-/Right-Invariant Vector Fields
- •3.3.1.2 Maurer-Cartan Forms on Lie Group Manifolds
- •3.3.1.3 Maurer Cartan Equations
- •3.3.2 Ehresmann Connections on a Principle Fibre Bundle
- •3.3.2.1 The Connection One-Form
- •Gauge Transformations
- •Horizontal Vector Fields and Covariant Derivatives
- •3.4 Connections on a Vector Bundle
- •3.5 An Illustrative Example of Fibre-Bundle and Connection
- •3.5.1 The Magnetic Monopole and the Hopf Fibration of S3
- •The U(1)-Connection of the Dirac Magnetic Monopole
- •3.6.1 Signatures
- •3.7 The Levi Civita Connection
- •3.7.1 Affine Connections
- •3.7.2 Curvature and Torsion of an Affine Connection
- •Torsion and Torsionless Connections
- •The Levi Civita Metric Connection
- •3.8 Geodesics
- •3.9 Geodesics in Lorentzian and Riemannian Manifolds: Two Simple Examples
- •3.9.1 The Lorentzian Example of dS2
- •3.9.1.1 Null Geodesics
- •3.9.1.2 Time-Like Geodesics
- •3.9.1.3 Space-Like Geodesics
- •References
- •4.1 Introduction
- •4.2 Keplerian Motions in Newtonian Mechanics
- •4.3 The Orbit Equations of a Massive Particle in Schwarzschild Geometry
- •4.3.1 Extrema of the Effective Potential and Circular Orbits
- •Minimum and Maximum
- •Energy of a Particle in a Circular Orbit
- •4.4 The Periastron Advance of Planets or Stars
- •4.4.1 Perturbative Treatment of the Periastron Advance
- •References
- •5.1 Introduction
- •5.2 Locally Inertial Frames and the Vielbein Formalism
- •5.2.1 The Vielbein
- •5.2.2 The Spin-Connection
- •5.2.3 The Poincaré Bundle
- •5.3 The Structure of Classical Electrodynamics and Yang-Mills Theories
- •5.3.1 Hodge Duality
- •5.3.2 Geometrical Rewriting of the Gauge Action
- •5.3.3 Yang-Mills Theory in Vielbein Formalism
- •5.4 Soldering of the Lorentz Bundle to the Tangent Bundle
- •5.4.1 Gravitational Coupling of Spinorial Fields
- •5.5 Einstein Field Equations
- •5.6 The Action of Gravity
- •5.6.1 Torsion Equation
- •5.6.1.1 Torsionful Connections
- •The Torsion of Dirac Fields
- •Dilaton Torsion
- •5.6.2 The Einstein Equation
- •5.6.4 Examples of Stress-Energy-Tensors
- •The Stress-Energy Tensor of the Yang-Mills Field
- •The Stress-Energy Tensor of a Scalar Field
- •5.7 Weak Field Limit of Einstein Equations
- •5.7.1 Gauge Fixing
- •5.7.2 The Spin of the Graviton
- •5.8 The Bottom-Up Approach, or Gravity à la Feynmann
- •5.9 Retrieving the Schwarzschild Metric from Einstein Equations
- •References
- •6.1 Introduction and Historical Outline
- •6.2 The Stress Energy Tensor of a Perfect Fluid
- •6.3 Interior Solutions and the Stellar Equilibrium Equation
- •6.3.1 Integration of the Pressure Equation in the Case of Uniform Density
- •6.3.1.1 Solution in the Newtonian Case
- •6.3.1.2 Integration of the Relativistic Pressure Equation
- •6.3.2 The Central Pressure of a Relativistic Star
- •6.4 The Chandrasekhar Mass-Limit
- •6.4.1.1 Idealized Models of White Dwarfs and Neutron Stars
- •White Dwarfs
- •Neutron Stars
- •6.4.2 The Equilibrium Equation
- •6.4.3 Polytropes and the Chandrasekhar Mass
- •6.5 Conclusive Remarks on Stellar Equilibrium
- •References
- •7.1 Introduction
- •7.1.1 The Idea of GW Detectors
- •7.1.2 The Arecibo Radio Telescope
- •7.1.2.1 Discovery of the Crab Pulsar
- •7.1.2.2 The 1974 Discovery of the Binary System PSR1913+16
- •7.1.3 The Coalescence of Binaries and the Interferometer Detectors
- •7.2 Green Functions
- •7.2.1 The Laplace Operator and Potential Theory
- •7.2.2 The Relativistic Propagators
- •7.2.2.1 The Retarded Potential
- •7.3 Emission of Gravitational Waves
- •7.3.1 The Stress Energy 3-Form of the Gravitational Field
- •7.3.2 Energy and Momentum of a Plane Gravitational Wave
- •7.3.2.1 Calculation of the Spin Connection
- •7.3.3 Multipolar Expansion of the Perturbation
- •7.3.3.1 Multipolar Expansion
- •7.3.4 Energy Loss by Quadrupole Radiation
- •7.3.4.1 Integration on Solid Angles
- •7.4 Quadruple Radiation from the Binary Pulsar System
- •7.4.1 Keplerian Parameters of a Binary Star System
- •7.4.2 Shrinking of the Orbit and Gravitational Waves
- •7.4.2.1 Calculation of the Moment of Inertia Tensor
- •7.4.3 The Fate of the Binary System
- •7.4.4 The Double Pulsar
- •7.5 Conclusive Remarks on Gravitational Waves
- •References
- •Appendix A: Spinors and Gamma Matrix Algebra
- •A.2 The Clifford Algebra
- •A.2.1 Even Dimensions
- •A.2.2 Odd Dimensions
- •A.3 The Charge Conjugation Matrix
- •A.4 Majorana, Weyl and Majorana-Weyl Spinors
- •Appendix B: Mathematica Packages
- •B.1 Periastropack
- •Programme
- •Main Programme Periastro
- •Subroutine Perihelkep
- •Subroutine Perihelgr
- •Examples
- •B.2 Metrigravpack
- •Metric Gravity
- •Routines: Metrigrav
- •Mainmetric
- •Metricresume
- •Routine Metrigrav
- •Calculation of the Ricci Tensor of the Reissner Nordstrom Metric Using Metrigrav
- •Index

4.3 The Orbit Equations of a Massive Particle |
165 |
Hence the first equation of (4.3.9) can also be rewritten as follows:
1 |
|
dr |
2 |
|
L2 |
|
m |
|
L2m |
|
E 2 − 1 |
(4.3.10) |
2 |
|
+ |
2r2 − r |
− |
r3 |
= |
2 |
|||||
|
dτ |
|
||||||||||
Equation (4.3.10) can be compared with the equation for energy conservation in the motion of a test particle of mass μ in the Newtonian field generated by a large mass M (see (4.2.1)). For motions that are sufficiently slow, we can identify:
dτ c dt |
(4.3.11) |
|
|
speed of light
so that, multiplying (4.3.10) by μ, we can rewrite it in the following way:
|
mμc2 |
+ |
1 |
μ |
dr |
2 |
|
|
1 L2c2μ |
|
c2L2mμ |
|
(E 2 |
− 1)c2μ |
(4.3.12) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||
− |
|
r |
|
|
|
2 |
|
|
dt |
|
|
+ 2 |
|
|
r |
|
− |
|
|
r |
|
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||||||||||||||
Furthermore, if the term c2L2mμ is much smaller than the other terms: |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2L2mμ |
1 L2c2μ |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
(4.3.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
then we can make the identifications: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2c2μ |
2 |
|
|
|
L |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
|
μc |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
mμ |
= GMμ |
|
|
m = |
GM |
|
(4.3.14) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
E 2 − 1 |
c2μ |
|
E |
|
|
|
|
E |
2 |
|
2E + μc2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
μc2 |
|
||||||||||||
or |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m = GMc2 |
|
= Schwarzschild emiradius |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
L |
|
|
μc |
|
|
|
|
angular momentum per unit mass per speed of light |
(4.3.15) |
||||||||||||||||||||||||||||||
|
|
= |
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
2 μcE2 |
total energy in rest mass units |
|
|
||||||||||||||||||||||||||||||||
E |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
This comparison with the Newtonian theory suggests the following bifurcation:
E |
< 1 |
bound state |
|
closed orbit |
(4.3.16) |
E |
> 1 |
unbound state |
|
open orbit |
|
4.3.1 Extrema of the Effective Potential and Circular Orbits
By means of (4.3.9) the problem of massive particle orbits in the Schwarzschild geometry has been formally reduced to the problem of classical motions in a central

166 |
4 Motion in the Schwarzschild Field |
potential. Hence, just as in classical Newtonian mechanics we have to study the extrema of the effective potential (4.3.9) in order to establish the conditions for stable and unstable circular orbits. Indeed if an orbit is circular we have dτdr = 0 and the radius r = r0 must be a root of the equation Veff (r) = E . The orbit will be stable if r0 is a minimum of the effective potential Veff , while it will be unstable if it is a maximum. Equating to zero the first derivative of Veff we obtain:
|
∂Veff |
|
m |
|
|
L2 |
mL2 |
|
||||
0 = |
|
|
= |
|
|
− 2 |
2r3 + 3 |
|
|
|
|
(4.3.17) |
∂r |
|
r2 |
r4 |
|
||||||||
with solutions: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 ± |
|
|
|
|
||||||
r |
|
L2(L2 − 12m) |
(4.3.18) |
|||||||||
|
|
|
|
|
|
|||||||
± = |
|
|
|
|
2m |
|
|
|
|
|
||
and considering the discriminant = L2(L2 − 12m) we conclude that for |
|
|||||||||||
|
|
|
L2 < 12m2 |
|
|
|
|
(4.3.19) |
||||
there are no extrema and consequently no stable orbits. Reinstalling physical units the stability bound (4.3.19) translates into:
r2 |
dϕ |
|
< √12 |
GM |
|
(4.3.20) |
|||||||||
dt |
c |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
In the case of test particles orbiting around the sun this means: |
|
||||||||||||||
|
R |
2 |
|
|
|
√ |
|
|
GM |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
< |
12 |
|
|
|
6 |
|
(4.3.21) |
||||||
|
|
|
|
2π |
|
|
c |
|
|||||||
|
T |
|
|
|
|
|
|
||||||||
where T and R are the period and radius of the orbit, respectively, and M6 denotes the mass of the sun. Inserting the numerical values of these physical constants we find:
GM6 |
= |
(6.670 cm3 s−2 g−1) |
|
4.43 |
· |
10 |
15 |
cm2 |
||||||||||||||||||
|
|
|
|
· |
|
|
10 |
|
|
|
|
− |
1 |
|
|
|
|
|
|
|||||||
|
c |
2.998 |
10 |
|
|
cm s |
|
|
= |
|
|
|
|
s |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 s = |
1 year |
|
|
= 3.1536 · 10−7 years |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
31, 536, 000 |
(4.3.22) |
|||||||||||||||||||||||||
|
|
|
1 km |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 cm2 = |
|
= 10−10 km2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1010 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
cm2 |
= |
1 |
|
|
|
· |
10−3 |
|
km2 |
|
0.317 |
· |
10−3 |
km2 |
|
||||||||||
s |
3.1536 |
|
year |
|||||||||||||||||||||||
|
|
|
|
|
· year = |
|
|
|
|
|
||||||||||||||||
Therefore the critical limit in the solar system is given by:
R2 |
≥ 1.7 · 10−4 |
km2 |
(4.3.23) |
T |
year |
4.3 The Orbit Equations of a Massive Particle |
167 |
It is instructive to compare condition (4.3.23) with the actual values of planetary radii or periods. The period of a planet is of the order of the year. Hence to be critical the radius of the orbit should be of the order of 10−2 km while, as we know, the typical distance of a planet from the sun is of the order of 108 km. Alternatively keeping the distance fixed, for instance inserting the average radius of the Earth orbit around the Sun:
r = 1.49 × 108 km |
(4.3.24) |
we obtain that a critical period for such a orbit would be Tcrit = 1020 years. In other words, in order to be critical, the Earth should be so slow as to make a full revolution in a time ten orders of magnitude longer than the age of the Universe
TUniverse ≈ 1010 years.
These numerical considerations give some appreciation of how far the solar system is from the critical phenomena implied by general relativity and explain why Newtonian mechanics works so well for the physical system it was invented to explain. Notwithstanding this smallness, the critical region is by no means irrelevant in astrophysical systems. Indeed, as we are going to see, it becomes quite important near compact stars whose mass is of the order of a stellar mass M6 but whose radius is of the order of the kilometer.
Minimum and Maximum The second derivative of the potential yields:
|
5 d2Veff |
2 |
|
|
|
2 |
|
|
2 |
|
|
||
r |
|
|
|
= 3L |
r − |
12mL |
|
− 2mr |
|
≡ J (r) |
(4.3.25) |
||
|
dr2 |
|
|
||||||||||
Inserting the values r± given in (4.3.18) we find: |
|
|
|
||||||||||
|
|
J (r+) > 0 |
|
r+ is a minimum |
(4.3.26) |
||||||||
|
|
J (r−) < 0 |
|
r− is a maximum |
|||||||||
|
|
|
|||||||||||
Explicitly we have: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 + |
|
> 6m |
|
||||||
|
|
r |
L2(L2 − 12m2) |
(4.3.27) |
|||||||||
|
|
|
|
||||||||||
|
+ = |
|
|
|
2m |
|
|
|
|
|
|
||
The important conclusion that we reach from (4.3.27) is that stable orbits exist only for radii r > 6m. In the case of the Sun the numerical value of the Schwarzschild emiradius reads:
|
|
|
GM6 |
|
|
|
||
|
m6 = |
|
c2 |
1.48 km |
|
|
(4.3.28) |
|
For L2 = 12m2 we have r− = 6m while the limit of r− for L2 → ∞ is: |
|
|||||||
|
|
L2 − |
|
|
|
|
||
lim r |
lim |
L2(L2 − 12m2) |
= |
3m |
(4.3.29) |
|||
|
2m |
|||||||
L2→∞ |
− = L2→∞ |
|
|
|
|
|
||
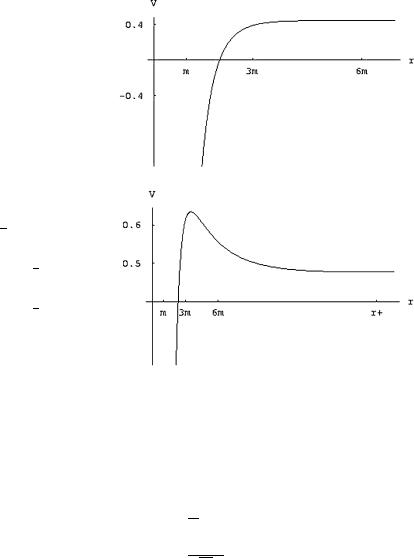
168 |
4 Motion in the Schwarzschild Field |
Fig. 4.6 Schwarzschild geometry: Plot of the
effective radial potential for= 1 L2 = 12m2. This is
the limiting case where no circular orbits are available. Indeed the potential has no extrema
Fig. 4.7 Schwarzschild geometry: Plot of the
effective√ potential for= 2 L2 = 24m2.
In this case the stable minimum of√the potential is at r+ = 6(2+ 2)m = 20.4853m, while the unstable
maximum is√at
r− = 6(2− 2)m = 3.51472m
It follows that the range of the root r− is:
3m < r− < 6m |
(4.3.30) |
and that is the range where unstable circular orbits are present.
In view of this analysis it is convenient to define the following dimensionless variables:
ρ = r m
(4.3.31)
= √ L
12m
and rewrite the effective potential (4.3.9) in terms of these:
Veff = |
1 |
− |
1 |
+ |
6 2 |
− |
12 2 |
(4.3.32) |
2 |
ρ |
ρ2 |
ρ3 |
The structure of the effective potential can be visualized by means of some plots. In Fig. 4.6 we display the limiting case L2 = 12m2 which admits no circular orbits. The reason is evident from the shape. In this case the potential has neither minima nor maxima. It just decreases from infinity towards infinitely large negative values
