Lorentz to look deeper into the transformation rules from one reference frame to another that are consistent with Maxwell equations.

1.2.3 Maxwell Equations and Lorentz Transformations

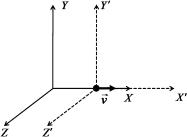
The equations of Newtonian mechanics are invariant under Galileo transformations that connect two relatively inertial systems. Let us denote by {t, x, y, z} the time and space coordinates of a certain physical event in the coordinate frame O and {t , x , y , z } those of the same event in the coordinate frame O . By hypothesis the two frames (or observers) are in relative motion with constant velocity v with respect to each other. Just for simplicity and without any loss of generality let us suppose that the relative motion of the two frames is along the x-axis as shown in Fig. 1.3. The dogma of Galilean-Newtonian Physics was that time is universal and the same for every one. So the Galileo transformation from one reference frame to the other is described by the following simple formula:

Analogous transformations can be written for all the other axes and, together with the rotations, the set of all Galileo transformations turns out to be a Lie group with six paramete‘rs given by the three Euler rotation angles and the three components of the relative velocity {vx , vy , vz}.

The astonishing discovery of Lorentz (see Fig. 1.4), published in his 1904 paper [3], is that Maxwell equations are not invariant under Galileo transformations, rather they are invariant against modified transformations that break the dogma of universal time and introduce the speed of light c. The special Lorentz transformation which replaces the Galileo transformation (1.2.11) is the following one:

Fig. 1.3 Two inertial reference frames moving with constant relative velocity along the x-axis

Fig. 1.4 Hendrik Antoon Lorentz (1853–1928) was Dutch by nationality. In 1902 the Nobel Prize in Physics was shared by Lorentz with Pieter Zeeman for the theoretical explanation of the phenomenon discovered by the latter and named after him. Hendrik Lorentz was born in Arnhem. He studied physics and mathematics at the University of Leiden, of which, later he became a professor. His doctoral degree was earned in 1875 under the supervision of Pieter Rijke with a thesis entitled “On the theory of reflection and refraction of light”, in which he refined the electromagnetic theory of James Clerk Maxwell. The proposal that moving bodies contract in the direction of motion was put forward by Lorentz in a paper of 1895 arriving at the same conclusion that had been reached also by George FitzGerald. Lorentz discovered that the transition from one reference frame to another could be simplified by using a new time variable which he called local time. In 1900, Henri Poincaré called Lorentz’s local time a “wonderful invention” and illustrated it by showing that clocks in moving frames are synchronized by exchanging light signals that are assumed to travel at the same speed against and with the motion of the frame. The transformations that we denote Lorentz transformations, following the name given to them by Poincaré in 1905, were published by Lorentz in a paper of 1904

where c is the speed of light and v the relative velocity of the two frames. It is evident from their mathematical form that when v c the Lorentz transformation is approximated extremely well by the Galileo transformation (1.2.11). Just as in the Galileo case, one can write similar transformations for the cases where the relative motion occurs along other axes and mix them with ordinary rotations, building up, at the end of the day, another six parameter group of transformations. Such a group has a simple mathematical name, i.e., SO(1, 3), since it contains all the 4 × 4 matrices that leave invariant a quadratic form with one positive and three negative eigenval-