Матрица C3[1 1 1] ортогонального преобразования с det C3[1 1 1] = +1 описывает поворот на 120°, так как tr C3[1 1 1] = 0, а собственным век-

тором матрицы C3[1 1 1] является [11 1].

При повороте вокруг [011] на 180о направление [100], будучи

перпендикулярным к [011], переходит в противоположное [1 00], а [010] →[001] и [001] →[010], и матрица имеет вид

1.3.2. Инверсионные оси

Кроме чистых вращений возможны также сочетания поворотных осей с отражением в лежащей на них точке. Подобные элементы симметрии называют инверсионными осями. Так как число поворотных осей ограничено (1, 2, 3, 4, 6), то инверсионные оси име-

ют тот же порядок и обозначаются 1, 2, 3, 4, 6 . Если отражение

происходит в точке, совпадающей с началом координат (центр инверсии), то матрица, описывающая это отражение, имеет вид

Умножая эту матрицу на матрицу поворота, например, вокруг оси ox (см. матрицу (1.86)), получаем матрицу несобственного (инверсионного) поворота

Определитель этой матрицы detRi = −1, а след матрицы инверсионного преобразования равен

63

Инверсионной оси 1 отвечает α = 0, эта ось эквивалентна центру инверсии. Для инверсионной оси второго порядка вдоль [100] соответствующая матрица, описывающая эту операцию, имеет вид

Очевидно, что при этой операции любая точка зеркально отображается относительно плоскости yz. Таким образом, инверсион-

ная ось 2 эквивалентна плоскости зеркального отражения или

плоскости симметрии, обозначаемой буквой m (от слова «mirror» − зеркало), расположенной перпендикулярно к этой оси.

Нетрудно убедиться, что ось 3 (α = 120°) эквивалентна осям 3 и 1 . Ось 6 эквивалентна осям 3 и 2 . Ось 4 является независимой, содержащей поворотную ось второго порядка 2.

Среди инверсионных осей независимыми являются 1, 2, 4 , а оси 3 и 6 составными: 3 = 3 +1 и 6 = 3 + 2 .

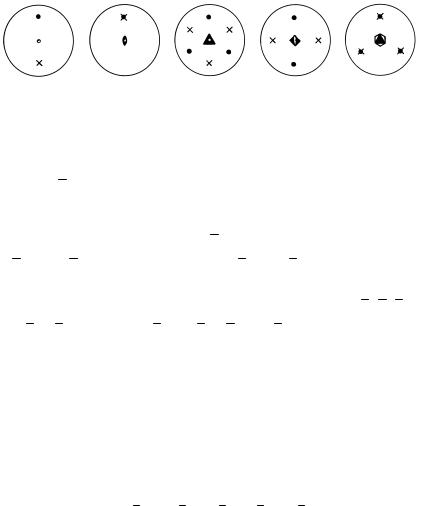
Изображение на стереографической проекции операций, отвечающих инверсионным осям, показано на рис. 1.41.

Рис. 1.41. Изображение инверсионных осей на стереографической проекции:

а – 1 ; б – 2 ; в – 3 ; г – 4 ; д – 6

1.3.3. Зеркально-поворотные оси

Инверсионные оси являются комбинацией центра инверсии и поворотных осей, но несобственное вращение может быть получено также комбинацией плоскости симметрии и поворотных осей,

64

Матрица, соответствующая зеркально-поворотной оси вдоль оси x, имеет вид

Определитель этой матрицы detRm = −1, а след матрицы зеркаль- но-поворотного преобразования равен

trRm = −1 + 2cosα. (1.91)

Важной характеристикой направлений в кристаллах является понятие полярности. Вдоль любой прямой можно двигаться в противоположные стороны. Если эти два направления равноценны, то прямая неполярна и преобразуется в себя какой-либо операцией, меняющей местами (совмещающей) ее противоположные «концы», например, плоскостью симметрии, перпендикулярной этой прямой или лежащей на ней центром симметрии. Так как оси симметрии являются прямыми, они могут быть полярными или неполярными. Так, инверсионные оси всегда неполярны, поворотные оси поляр-

ны, если они не пересекаются с элементами симметрии 1 , m, 2.

Полярности направлений в кристаллах соответствует полярность физических свойств.

1.3.4. Элементы теории групп

Рассмотрение комбинаций закрытых элементов симметрии полезно проводить с использованием теории групп.

Абстрактная группа G есть множество объектов {g1, g2, . . .}, называемых элементами группы, которые должны удовлетворять четырем постулатам:

1) на группе задана операция, называемая умножением, когда любым элементам группы gi и gj ставится в соответствие третий

65

3) существует один и только один элемент e, называемый единичным элементом, такой, что для любого элемента группы

4) для любого элемента gi существует обратный элемент gi–1, такой, что

Из рассмотрения групповых постулатов следует, что групповое умножение не обязательно связано с арифметическим или алгебраическим умножением.

При умножении не всегда выполняется коммутативный закон умножения, т.е. произведение gigj (операция gj с последующей операцией gi) не обязательно равно произведению gjgi (операция gi с последующей операцией gj); группа, в которой выполняется коммутативный закон умножения gigj = gjgi, называется абелевой.

Число элементов n в группе называется порядком группы. Порядок группы может быть конечным или бесконечным. Если в группе порядка n можно найти m элементов, также удовлетворяющих групповым постулатам, то эти элементы образуют подгруппу исходной группы. Любая подгруппа содержит единичный элемент. Порядок подгруппы m является делителем порядка группы n (теорема Лагранжа). Следовательно, группа, порядок которой является простым числом, не имеет подгрупп, кроме тривиальных (E и самой группы).

Если r − наименьшее целое число, для которого gr = e, то r называют порядком элемента g, а r элементов g, g2, …, gr–1, gr = e образуют период g. Период любого элемента конечной группы есть или сама группа, которая в этом случае называется циклической, или подгруппа циклической группы, содержащей этот элемент. В циклической группе все элементы исчерпываются степенями одного, называемого генератором группы. Если группа не является циклической, то в ней можно выделить несколько элементов − генераторов группы, степени и произведения которых дают все элементы группы.

Рассмотрим несколько примеров групп.

66

1.Множество целых чисел, которое включает в себя числа положительные, отрицательные и нуль. Групповое действие − сложение, единичный элемент − нуль, обратным элементом для числа n является противоположное число –n, порядок группы − бесконечный, группа − абелева.

2.Множество рациональных чисел типа p/q, где p, q − целые числа и q ≠ 0. Групповое действие − умножение, единичный элемент − единица, обратным элементом для числа n является обратное число 1/n, порядок группы − бесконечный, группа − абелева.

3.Множество матриц размерности n×n с определителем, не равным нулю. Групповое действие − умножение матриц, единичный элемент − единичная матрица n×n, обратный элемент − обратная матрица, порядок группы − бесконечный, группа − не абелева.

4.Группа операций вращения тела вокруг произвольной оси. Единичный элемент − отсутствие вращения или вращение на 2π. Обратный элемент − операция вращения в противоположном направлении, порядок группы − бесконечный, группа − не абелева.

Группы называют изоморфными, если между элементами двух групп G и H устанавливается взаимно однозначное соответствие. Изоморфные группы тождественны между собой с точки зрения их абстрактных свойств. Различие состоит лишь в том, что элементы групп пронумерованы по-разному. Если каждому элементу группы G соответствует элемент группы H без требования взаимной однозначности, то группы называют гомоморфными. Следовательно, одному элементу группы H может соответствовать несколько элементов группы G.

Элемент группы gi называется сопряженным элементу gk, если в G есть такой элемент gj, что

Множество взаимно-сопряженных элементов в группе образует

класс сопряженных элементов. Единичный элемент сам по себе образует класс сопряженных элементов.

Свойства группы отражаются в групповой таблице умножения (таблица Кэли). Для ее построения все элементы группы записывают по вертикали и по горизонтали. Групповая таблица состоит из результатов попарных произведений, у которых первый множитель

67