|
|
а |
б |
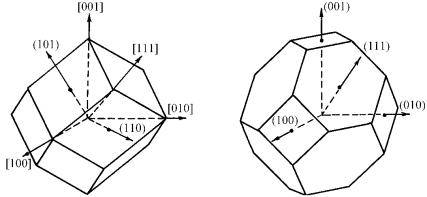
Рис. 1.37. Ячейки Вигнера–Зейтца для ГЦК (а) и ОЦК кристаллов (б)
В физике твердого тела фундаментальное значение имеет ячейка Вигнера−Зейтца, построенная для обратной решетки. Эта ячейка называется зоной Бриллюэна. Как известно, ГЦК и ОЦК решетки являются взаимно обратными и, следовательно, зона Бриллюэна для ГЦК решетки изображается многогранником с 14 гранями, а зона Бриллюэна для ОЦК решетки − правильным ромбическим додекаэдром.
1.3. Симметрия кристаллов
Симметрия кристаллического пространства определяется заданием всех преобразований, которые сохраняют расстояния между любыми точками пространства и приводят к совмещению пространства с самим собой. Элементы симметрии делят на закрытые и открытые. Открытые элементы симметрии содержат трансля-
ции и поэтому описывают симметрию бесконечного пространства. Закрытые элементы симметрии оставляют одну точку неподвижной и после конечного числа операций возвращают кристаллическое пространство в исходное положение. Закрытые элементы симметрии задаются матрицами ортогонального преобразования R с detR = ± 1. Они могут быть сведены к поворотным осям симмет-
рии (чистое или собственное вращение с detR = + 1) и к инверси-
59
онным осям (вращение с отражением в точке, лежащей на оси, или несобственное вращение с detR = − 1).
1.3.1. Поворотные оси симметрии
Осью симметрии называют прямую, при повороте вокруг которой на некоторый угол αn гомологические (эквивалентные) точки кристаллического пространства совмещаются. Угол поворота αn равен 360о/n, где n − целое число. Значит, через n поворотов в одном направлении на угол αn кристаллическое пространство возвращается в исходное положение. Наименьший угол поворота αn для данной оси симметрии называют элементарным углом оси симметрии, а n − порядком оси поворота. В кристаллографической системе координат при повороте вокруг оси симметрии произвольный вектор x, задающий узел пространственной решетки, переходит в вектор x′:
x′ = Rx,
где R − матрица вращения, а x и x′ − векторы-столбцы. Координатами векторов x и x′, определяющих узлы пространст-
венной решетки в кристаллографической системе координат, являются целые числа, поэтому компонентами матрицы R и, следовательно, ее следа trR также являются целочисленные величины, т.е. trR = N, где N − целое число.
В ортогональной системе координат преобразование R будет описываться матрицей подобия R′ = CRC-1, где C − матрица перехода от кристаллографической системы координат к ортогональной системе. Если ортогональную систему координат выбрать таким образом, чтобы ось симметрии совпала с осью x, то поворот вокруг этой оси будет описываться матрицей R′ вида
1 |
0 |
0 |
|
|
|
0 |
cosα |
|
(1.86) |
R′ = |
− sinα |
|||
|
0 |
sinα |
|
|
|
cosα |
|
||
След этой матрицы trR′ = trR = N = 1 + 2 cosα; N может принимать значения 0, ±1, +2, +3. Отсюда следует, что возможны лишь повороты на угол α, равный 0, 60, 90, 120 и 180° (табл. 1.2). Таким
60
образом, в кристаллическом пространстве возможны оси симметрии первого, шестого, четвертого, третьего и второго порядков.
Таблица 1.2
Расчет поворотных осей симметрии
|
След матрицы |
cosα |
α, град. |
Порядок |
|
|
поворота trR |
|
|
поворотной оси n |
|
|
−1 |
−1 |
180 |
2 |
|
|
0 |
−1/2 |
120 |
3 |
|
|
+1 |
0 |
90 |
4 |
|
|
+2 |
1/2 |
60 |
6 |
|
|
+3 |
1 |
0, 360 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
в |
г |
д |
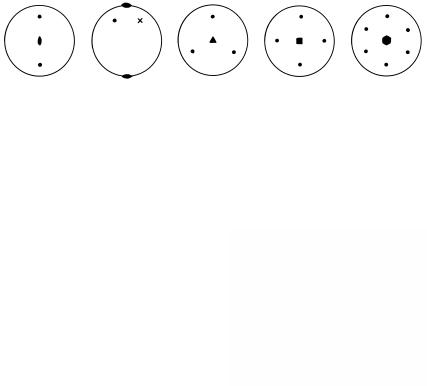
Рис. 1.38. Изображение поворотных осей на стереографической проекции: а − ось 2-го порядка перпендикулярна плоскости проекции; б − ось 2-го порядка
параллельна плоскости проекции; в, г, д − оси 3-го, 4-го и 6-го порядка соответственно перпендикулярны плоскости проекции
Отсутствие осей пятого порядка в трехмерном или 3D- пространстве связано, как следует из предыдущих рассуждений, с наличием в кристаллическом пространстве трансляционной симметрии. Оси пятого порядка появ-
ляются в 4D-пространстве.
Изображение операций, отве- |
|
чающих поворотным осям сим- |
|
метрии 2, 3, 4, 6 порядков показано |
|
на рис. 1.38. |
|
В кристаллах с ГЦК решеткой |
|
осями второго порядка являются |
|
направления <110>, осями третье- |
|
го порядка − <111>, осями четвер- |
Рис. 1.39. Основные оси симметрии |
того порядка <100> (рис. 1.39). |
в кубической сингонии |
61
Матрицы поворотных элементов симметрии. Компоненты матрицы поворотного элемента симметрии можно получить с использованием стандартной стереографической проекции. Если оси системы координат xyz совпадают с направлениями [100], [010] и [001], то, как было показано, компонентами матрицы поворота будут индексы направлений <100> после поворота.
При повороте вокруг оси [100] на 90о против часовой стрелки, как показано на рис. 1.40, направление [100] остается на месте, а направления [010] и [001], перемещаясь по основному кругу про-
екции, переходят в [001] и [01 0] соответственно. Таким образом, компонента-
ми матриц-столбцов C4[100] бу-
|
|
|
|
|
|
|
|
|
|
|
|
дут (100), (001) и (01 0), и матри- |
|
|
|
||||||||
ца C |
[100] будет иметь вид |
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
[100] |
1 |
0 |
|
0 |
|
|
|
|||
|
|
0 |
0 |
|
|
|
|
|
|||
|
C4 |
= |
|
−1 . |
|
|
|
||||
|
|
|
0 |
1 |
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
||||
Действительно |
C[100]− мат- |
|
|
|
|||||||
|
|
|
|
4 |
|
|
|
|
|||
рица |
ортогонального |
преобразо- |
Рис. 1.40. Траектории движения |
||||||||
вания с det C4[100]= +1 описывает |
|||||||||||
при поворотах вокруг [100], [1 |
|
1], |
|||||||||
1 |
|||||||||||
поворот на 90о, так как |
tr C4[100] = |
[011] в кубической сингонии |
|||||||||
|
|
|
|||||||||
= +1, вокруг [100], поскольку для λ = 1 собственным вектором матрицы C4[100] является [100].
Точно так же при повороте вокруг [11 1] на 120о против часовой
стрелки направление [100] переходит в [001], [01 0] − в [100], т.е.
[010]→[1 00], а [001]→[01 0]. Соответствующая матрица имеет вид
|
|
|
0 |
−1 |
0 |
||
[1 |
|
1] |
|
|
|
|
|
1 |
0 |
0 |
|
||||
C3 |
= |
−1 . |
|||||
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|||
62