Так, структура (2×2) встречается у никеля при обнажении грани (111) при наличии кислорода: Ni(111)–(2×2)O. Структура поверхности (110) вольфрама записывается как W(110)–C(9×5)CO; ячейка Бравэ − центрированная прямоугольная. У кремния чистая поверхность (100) имеет структуру (2×1), а при наличии адсорбированного водорода восстанавливается прежняя периодичность (1×1): Si(100)–(1×1)H.

В табл. 1.5 приведены некоторые данные о реконструкции и релаксации чистых металлических поверхностей в ГЦК кристаллах.

Данных о структуре поверхности тугоплавких ОЦК кристаллов пока немного: Cr(100)–( 2 × 2 ), Mo(100)–( 2 × 2 ), W(100)–

( 2 × 2 ), V(100)–(5×1). Релаксация поверхности (100) связана со сжатием на ~ 5 ÷ 10% для W, на ~ 11% для Mo, на ~ 1,4% для Fe,

релаксация поверхности (110) незначительна, а поверхность (111) для Fe связана со сжатием на ~ 15%.

Изучение структуры поверхности проводят с помощью дифракции медленных электронов с энергией ~ 10−100 эВ.

1.5. Физические свойства кристаллов

Изучением физических свойств кристаллов занимается специальный раздел кристаллографии − кристаллофизика. Математический аппарат кристаллофизики основан на тензорном исчислении и на теории групп. Вследствие макроскопических свойств (однородности, симметрии и анизотропии) в кристаллах обнаруживается ряд свойств, невозможных в изотропных телах. Задачей кристаллофизики является установление влияния симметрии на физические

105

свойства кристаллов, а также изучение влияния внешних воздействий на свойства кристаллов.

1.5.1. Принцип симметрии в кристаллофизике

Поскольку для любого макроскопического свойства кристалл рассматривается как однородная среда, то совершенно несущественны различия между простыми и винтовыми осями, между зеркальными плоскостями и плоскостями скользящего отражения. Таким образом, симметрия макроскопических свойств кристаллов определяется не пространственной, а точечной группой симметрии кристалла. Это соответствует известному принципу Неймана, современная формулировка которого гласит: «Элементы симметрии любого физического свойства кристалла должны включать элементы симметрии точечной группы кристалла».

На языке теории групп принцип Неймана означает, что группа симметрии любого свойства кристалла включает в себя группу симметрии самого кристалла, т.е. группа симметрии кристалла либо совпадает с группой симметрии свойства, либо является подгруппой последней:

и симметрия физического свойства не ниже симметрии кристалла. Соотношению (1.104) должна удовлетворять группа симметрии любого свойства кристалла. Если рассмотреть достаточно обширный набор различных свойств некоторого кристалла, то единственными общими элементами симметрии всех свойств, входящих в этот набор, окажутся элементы симметрии точечной группы кристалла. Таким образом, точечная группа кристалла оказывается пересечением (общей частью) групп симметрии всевозможных свойств этого кри-

сталла.

Если на кристалл накладывается физическое воздействие, обладающее определенной симметрией, то симметрия такого кристалла, находящегося в поле воздействия, изменяется и может быть опре-

делена при помощи принципа суперпозиции Кюри.

Кристалл, находящийся под влиянием внешнего воздействия, сохраняет лишь те элементы симметрии, которые являются общи-

106

ми для кристалла без воздействия и для воздейстия без кристалла. Кристалл под внешним воздействием изменяет свою точечную симметрию так, что сохраняет лишь элементы симметрии, общие с элементами симметрии воздействия. Иными словами, точечная группа симметрии кристалла Gкр в результате воздействия переходит в Gкр.возд − высшую общую подгруппу групп симметрии кристалла Gкр и воздействия Gвозд при заданной взаимной ориентации элементов симметрии этих групп, т.е. Gкр.возд есть пересечение групп Gкр и Gвозд:

Для определения симметрии результирующего явления важна не только симметрия взаимодействующих явлений, но и взаимное расположение их элементов симметрии. При решении такого рода задач удобно пользоваться стереографическими проекциями точечных групп симметрии кристаллов.

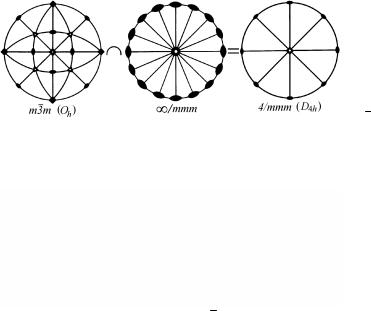
Рассмотрим, например, воздействие одноосного механического растягивающего усилия на кристалл класса m 3 m. Растягивающее усилие относится к одной из предельных групп симметрии Кюри ∞/mmm, т.е. симметрии покоящегося цилиндра. Если это усилие направлено вдоль одной из осей 4, то, как видно из рис. 1.72, сохраняются лишь общие элементы симметрии: одна ось 4, четыре поперечные оси 2, четыре продольные и одна поперечная плоскости m и центр симметрии. В результате кубический кристалл m 3 m под действием механического растяжения вдоль оси 4 приобретает свойства тетрагонального кристалла класса 4/mmm.

Рис. 1.72. Изменение симметрии кристалла m 3 m под действием одноосного растяжения вдоль [100]

107

Если к тому же кристаллу приложить то же усилие вдоль одной из его осей 3, то останутся только общие элементы симметрии: ось 3, три продольные плоскости симметрии m, три поперечные оси 2 и

центр симметрии, т.е. кристалл станет тригональным класса 3 m. Действие электрического поля повлияет на симметрию кристал-

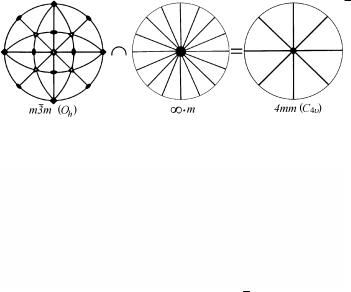
ла не так, как действие механического напряжения, потому что симметрия электрического поля и механического усилия различны. Симметрию однородного электрического поля можно изобразить как симметрию неподвижного конуса ∞m. Под действием электрического поля вдоль оси 4 кристалл m 3 m переходит в кристалл класса 4mm (рис. 1.73), а под действием электрического поля вдоль оси 3 − в 3m.

Рис. 1.73. Изменение симметрии кристалла m 3 m под действием электрического поля вдоль [100]

Заметим, что принцип суперпозиции симметрии нельзя применить для решения обратного вопроса, т.е. по симметрии результирующего явления нельзя судить о симметрии вызвавших его причин.

Иногда используют обобщенный принцип суперпозиции Кюри: когда несколько различных явлений природы накладываются друг на друга, образуя одну систему, их диссиметрии складываются.

Под диссимметрией, по А.В. Шубникову, следует понимать отсутствующие элементы симметрии.

1.5.2. Тензорное описание физических свойств кристаллов

Кристаллофизические системы координат. Для описания фи-

зических свойств кристаллов используют правую прямоугольную

108

систему координат. Для кубической, тетрагональной и ромбической сингоний оси этой кристаллофизической системы координат x1, x2, x3 совпадают с кристаллографическими осями x, y, z. Для остальных сингоний кристаллофизические оси ориентированы относительно кристаллографических по правилам стандартной установки (табл. 1.5)

Таблица 1.5

Правила кристаллофизической установки

Когда на кристалл оказывается воздействие и возникает ответное явление (эффект), физическое свойство кристалла появляется в виде соотношения

Если воздействие и вызванное им явление изотропны, то и соответствующее свойство кристалла изотропно, т.е. скалярно. Скалярные величины (тензоры нулевого ранга) не меняются при переходе от одной системы координат к другой. Таковы, например, масса, плотность, температура, теплоемкость, внутренняя энергия, энтропия.

Если при изотропном (скалярном) воздействии на кристалл возникающее явление имеет векторный характер, то соответствующее свойство кристалла − векторное. Так, в кристаллах 10 полярных классов возможен пироэлектрический эффект: под действием однородного изменения температуры (скалярное воздействие) кристалл электризуется; возникающее электрическое поле характеризуется вектором поляризации P. В соответствии с соотношением

109

(1.106) физическое свойство задается векторной величиной коэффициента пироэлектрического эффекта.

Свойства кристалла, связывающие воздействие и явления по схеме (1.106), могут описываться также тензорами второго, третьего и четвертого рангов.

Тензор второго ранга A имеет девять (32) независимых компонентов Aij. При переходе от прямоугольной системы координат x1, x2, x3 к новой прямоугольной системе x1′ , x′2 , x3′ , повернутой на

угол φ и имеющей общее начало, компоненты тензора второго ранга преобразуются по закону

Введем следующее правило суммирования (по Эйнштейну): ес-

ли в одном и том же члене индекс повторяется дважды, то автоматически подразумевается суммирование по этому индексу.

Теперь соотношение (1.107) имеет вид

Тензор A симметричен, если Aij = Aji, и антисимметричен, если

Aij = −Aji.

Такие физические свойства кристалла, как удельная электропроводность, удельное электросопротивление, коэффициенты теплопроводности, тепловое сопротивление, диэлектрические проницаемость и восприимчивость, магнитные проницаемость и восприимчивость являются симметричными тензорами второго ранга.

Тензорные свойства проявляются также при тензорных воздействиях. Так, к тензорам третьего ранга относится коэффициент Холла, а к тензорам четвертого ранга − коэффициенты упругости, магнитострикции. Тензор четвертого ранга имеет 34 = 81 независимую компоненту. Однако число компонентов тензора упругости изза симметрии тензоров деформации и напряжения сокращается с 81 до 36, а из-за термодинамических соображений число их уменьшается до 21. Дальнейшее уменьшение связано с симметрией кристалла, так что в кубической сингонии их всего три.

110

1.5.3. Влияние симметрии кристалла на его свойства, описываемые тензорами второго ранга

Симметрия физического свойства в соответствии с принципом Неймана не ниже симметрии кристалла. Но симметрия свойства, описываемого тензором второго ранга, всегда выше на центр симметрии. Рассмотрим это на примере тензора удельной электропроводности.

Тензор удельной электропроводности σ появляется, когда к кристаллу приложено электрическое поле, заданное вектором E, и по проводнику течет ток с плотностью j:

где σij − компоненты тензора σ. При изменении направлений векторов E и j компоненты σij остаются неизменными, т.е. тензор σ обладает центром симметрии.

Все свойства, описываемые тензорами второго ранга, являются центросимметричными.

В триклинных кристаллах симметричный тензор второго ранга имеет 6 независимых коэффициентов.

Если в кристалле появляется поворотная ось второго порядка вокруг оси y, задаваемая поворотной матрицей C2y, то компоненты тензора σ преобразуются в σ′ как

111

Поскольку тензор σ инвариантен относительно преобразования симметрии C2y, то σ′ = C2yσC2−y1 = σ и, как видно из (1.111), σ12 =

= − σ12, σ23 = − σ23, что может быть при условии σ12 = σ23 = 0. Таким образом, в моноклинных кристаллах симметричные тен-

зоры второго ранга имеют четыре независимых коэффициента σ11,

σ22, σ33, σ13.

В ромбических кристаллах из-за осей C2x и C2z остаются три ко-

эффициента σ11, σ22, σ33.

Для кубических кристаллов с точечной группой Т(23) из-за оси

Теперь σ11 = σ22 = σ33 = σ, т.е. в кубических кристаллах симметричный тензор второго ранга имеет один независимый коэффициент.

Тензоры в зависимости от их отношения к объекту бывают двух различных типов: тензоры, описывающие свойства кристалла, т.е. соотношения между измеряемыми величинами, − так называемые материальные тензоры и тензоры, описывающие воздействие на кристалл и его реакцию, − так называемые полевые тензоры.

Симметрия материальных тензоров должна в соответствии с принципом Неймана согласовываться с симметрией кристалла. В противоположность материальным тензорам симметрия полевых тензоров не связана с симметрией кристалла. Например, можно к кристаллу любой симметрии приложить как угодно ориентированное электрическое поле (полярный вектор) или механическое напряжение (симметричный полярный тензор 2-го ранга); точно так-

112