
- •от ХХ УУУУ 20007 г. МГУП
- •Учебник подготовлен в рамках Инновационной образовательной программы
- •ISBN 978-5-7262-0821-3
- •ISBN 978-5-7262-0822-0 (т.1)
- •Глава 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
- •Предисловие к тому 1
- •Глава 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
- •1.1. Кристаллическое состояние
- •1.1.3. Решетка и структура кристаллов
- •1.2. Основы кристаллографии
- •1.2.1. Кристаллографические проекции
- •1.2.2. Пространственная решетка
- •1.2.3. Кристаллографические символы
- •1.2.4. Обратная решетка
- •1.2.5. Матрица ортогонального преобразования
- •1.2.6. Преобразование индексов направлений
- •1.3. Симметрия кристаллов
- •1.3.1. Поворотные оси симметрии
- •1.3.2. Инверсионные оси
- •1.3.3. Зеркально-поворотные оси
- •1.3.4. Элементы теории групп
- •1.3.5. Точечные группы симметрии
- •Бравэ
- •Бравэ
- •Распределение ячеек Бравэ по сингониям показано в табл. 1.4.
- •1.3.6. Пространственные группы
- •1.3.7. Предельные группы симметрии
- •1.4. Структура кристаллов
- •1.4.1. Плотнейшие упаковки в структурах
- •1.4.3. Структурные типы соединений типа АВ
- •1.4.4. Структурные типы соединений типа АВ2
- •1.4.5. Структурные типы соединений типа АmВnCk
- •1.4.7. Структура фуллеренов, фуллеритов
- •1.4.8. Структура поверхности
- •1.5. Физические свойства кристаллов
- •1.5.1. Принцип симметрии в кристаллофизике
- •1.5.4. Упругие свойства кристаллов
- •1.6. Кристаллография пластической деформации
- •1.6.1. Геометрия пластической деформации
- •1.6.2. Кристаллографическая текстура
- •1.7. Кристаллография границ зерен
- •1.7.1. Малоугловые границы
- •1.7.2. Высокоугловые границы
- •1.8. Кристаллография мартенситных превращений
- •1.8.1. Морфология мартенситных превращений
- •1.8.2. Кристаллография мартенситных превращений
- •Контрольные вопросы, задачи и упражнения
- •Глава 2. ДЕФЕКТЫ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ
- •2.1. Точечные дефекты
- •2.1.1. Вакансии и межузельные атомы
- •2.1.2. Энергия образования точечных дефектов
- •Контрольные вопросы
- •Список использованной литературы
- •Глава 3. ФИЗИКА ТВЕРДОГО ТЕЛА
- •3.1. Строение атомов и межатомные взаимодействия
- •3.1.1. Классификация конденсированных систем
- •3.1.4. Энергия связи кристаллов
- •3.1.5. Типы связи в твердых телах
- •Металлическая связь. В отличие от ковалентной связи, которая образуется между двумя соседними атомами в результате коллективизации двух валентных электронов, металлическая связь появляется вследствие коллективизации всех валентных электронов. Эти электроны не локализуются у отдельных атомов, а принадлежат всему коллективу атомов. Поэтому они называются свободными электронами, перемещающимися по всему объему металла и в каждый момент времени равномерно распределенными в нем. Классическим подтверждением наличия таких свободных электронов в металлах является опыт Мандельштама и Папалекси, когда при резкой остановке вращающейся катушки, сделанной из металлической проволоки, в ней возникал электрический ток. Ярким подтверждением этому являются высокие электро- и теплопроводность металлов.
- •Ионная связь. Атомы, стоящие в периодической системе Д. И. Менделеева рядом с инертными газами, обладают склонностью принимать их конфигурацию либо путем отдачи, либо путем принятия электронов. У атомов щелочных металлов, стоящих непосредственно за инертными газами, валентный электрон слабо связан с ядром, так как движется вне заполненного слоя. Поэтому этот электрон может быть легко удален от атома. У галоидов, стоящих непосредственно перед инертными газами, недостает одного электрона для заполнения устойчивого слоя благородного газа. Поэтому галоиды обладают высоким сродством к дополнительному электрону.
- •Изоморфизм и морфотропия. Рассмотрим несколько ионных соединений щелочных металлов с галоидом бромом: LiBr, NaBr, KBr, RbBr и CsBr. Первые четыре соединения имеют решетку типа NaCl, а пятое соединение CsBr кристаллизуется в решетке типа CsCl.
- •3.2. Основы электронной теории кристаллов
- •3.2.1. Квантовая теория свободных электронов
- •3.2.2. Зонная теория металлов
- •3.3. Теория фаз в сплавах
- •3.3.1. Классификация фаз в сплавах
- •3.3.2. Твердые растворы
- •3.3.3. Промежуточные фазы
- •1B3.4. Диффузия и кинетика фазовых превращений
- •2Bв металлах и сплавах
- •4B3.4.1. Линейные феноменологические законы
- •5B3.4.2. Макроскопическое описание явления диффузии
- •6B3.4.3. Атомная теория диффузии в металлах
- •9B3.4.5. Диффузия и фазовые превращения в металлах
- •10Bи сплавах
- •3B3.5. Электрические свойства твердых тел
- •11B3.5.1. Основы электронной теории электропроводности
- •14B3.5.3. Эффект Холла
- •15B3.5.4. Связь электросопротивления со строением сплавов
- •20B3.5.7. Сверхпроводимость
- •3.6. Магнитные свойства твердых тел
- •3.6.1. Основные определения. Классификация веществ по магнитным свойствам
- •3.6.2. Магнитные свойства свободных атомов
- •3.6.3. Физическая природа диамагнетизма
- •3.6.4. Физическая природа парамагнетизма
- •3.6.5. Магнитная восприимчивость слабых магнетиков
- •3.6.6. Основы теории магнитного упорядочения
- •3.6.7. Доменная структура ферромагнетиков
- •3.6.8. Магнитные свойства ферромагнетиков
- •3.6.9. Антиферромагнетики и ферримагнетики
- •3.7. Тепловые свойства твердых тел
- •3.7.2. Теплоемкость кристаллических твердых тел
- •3.7.3. Теплопроводность твердых тел
- •3.7.4. Термическое расширение твердых тел
- •3.8. Упругие свойства твердых тел
- •3.8.1. Основные характеристики упругости
- •3.8.2. Упругость чистых металлов и сплавов
- •3.8.3. Ферромагнитная аномалия упругости
- •3.8.5. Внутреннее трение
- •Контрольные вопросы
- •Список использованной литературы
3.4.2. Макроскопическое описание явления диффузии
Кинетику диффузионных процессов изучают, рассматривая твердое тело как сплошную среду, т.е. пренебрегая его атомной структурой. Основным уравнением, описывающим поведение этой среды, является гидродинамическое уравнение непрерывности:
∂C |
+ divJ = 0 , |
(3.17) |
|
∂t |
|||
|
|
где С – концентрация и J – поток вещества.
Основные дифференциальные уравнения диффузии были предложены А. Фиком на основании обобщения уравнений теплопроводности. Последующее развитие физики твердого тела не внесло изменений в сформулированные им законы.
Феноменологические уравнения диффузии. В процессе отжи-
га неоднородного однофазного сплава возникает поток вещества, стремящийся уменьшить градиент концентрации. В случае, если градиент концентрации i-го компонента направлен по оси x, поток этого компонента через единичную площадь в единицу времени вдоль оси х
J |
|
= −D |
∂Ci |
, |
(3.18) |
|
|
||||
|
i |
i |
∂x |
|
|
где Di – коэффициент диффузии i-го компонента (далее индекс i
опускается).
Это уравнение называют первым законом Фика. Для трехмерной задачи первое уравнение Фика имеет вид:
J = −D C . (3.19)
Размерность потока в этом уравнении зависит от размерности концентрации. Размерность коэффициента диффузии [D] = м2/с. Од-
нако в большинстве монографий и справочников приводится [D] = = см2/с.
Совместное использование уравнений (3.17) и (3.18) дает второе уравнение Фика, описывающее изменение концентрации диффундирующего вещества впространстве и во времени:
∂C |
|
∂ |
∂C |
|
|
∂t |
= − |
|
D |
. |
(3.20) |
|
|||||
|
∂x |
∂x |
|
||
429

Решение второго уравнения диффузии для частных случаев.
Стационарные решения. Второе уравнение диффузии представляет собой дифференциальное уравнение в частных производных. Для его решения необходимо сформулировать начальные и граничные условия, которым должна удовлетворять концентрация диффундирующего вещества. Для трехмерной задачи уравнение (3.16) принимает вид:
|
∂C |
= D 2C , |
|
|
|
|
|
|
|
(3.21) |
||||
|
|
|
|
|
|
|
|
|
||||||
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
где 2 = divgrad – оператор Лапласа. |
|
|
|
|
|
|
|
|
|
|
||||
В стационарном состоянии |
∂C / ∂t = 0 и |
необходимо |
решить |
|||||||||||
уравнение D 2C = 0 . В простейшем случае для одномерной задачи |
||||||||||||||
уравнение имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||
прямоугольные координаты – |
|
D(∂2C / ∂x2 ) = 0 ; |
|
|
|
|||||||||
|
|
|
|
|
∂ 2 C |
|
1 |
∂C |
|
|
|
|||
цилиндрические координаты – |
|
|
|
2 |
+ |
|
|
|
= 0 ; |
(3.22) |
||||
D |
∂r |
r |
∂r |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂2C |
2 |
|
∂C |
|
|
|
|
|||
сферические координаты – D |
|
|
|
|
|
|
|
|
= 0 . |
|
|
|
||
∂r2 |
+ r |
∂r |
|
|
|
|
||||||||
Нестационарные решения для бесконечно тонкого слоя
диффундирующего вещества. Если величина |
D не зависит от |
||||
координат, то уравнение (3.20) принимает вид: |
|
||||
∂C |
= D |
∂2C |
. |
(3.23) |
|
∂t |
∂x2 |
||||
|
|
|
|||
В случае, когда некоторое количество α |
диффундирующего |
||||
вещества (диффузанта) нанесено в виде бесконечно тонкого слоя h наторцевую поверхность образца, после чего система подвергается диффузионному отжигу в течение времени t, решение уравнения (3.23), получаемое с помощью метода разделения переменных, имеет вид:
C(x,t) = |
|
α |
exp(− |
x2 |
), |
(3.24) |
|
πDt |
4Dt |
||||
2 |
|
|
|
|||
где х – расстояние по нормали к исходному слою; α = С0h (С0 – начальная концентрация диффузанта на поверхности). При этом
430
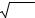
предполагается, что начальное распределение диффузанта можно представить δ-функцией и в любой сколь угодно малый промежуток времени все диффундирующее вещество способно полностью раствориться в объеме. Полное количество растворенного вещества можно определить по формуле
∞
α = ∫C(x,t)dx .
−∞
Если после диффузионного отжига образец секционировать на тонкие слои, параллельные исходной поверхности, то после измерения концентрации диффузанта в каждом слое, отвечающем некоторому
значению x , можнопостроитьграфикзависимости ln C от x2 . Из уравнения (3.20) следует, что это – прямая линия, тангенс угла наклона
которойравен (4Dt)−1 , откуда, зная t , можно определить D .
В этом методе определения D , как правило, в качестве диффузанта используют радиоактивные изотопы, значительно повышающие чувствительность определения концентрации. Кроме того, только с помощью этого метода «меченых атомов» можно определять коэффициенты самодиффузии в чистых металлах и диффузии компонентов в сплавах (далее в тексте коэффициенты диффузии
«меченых атомов» будут обозначаться D ).
Основной вариант метода снятия слоев с использованием измерения интегральной радиоактивности оставшейся части образца развит в нашей стране. В этом методе, предложенном П. Л. Грузиным, интегральная радиоактивность J (xn ,t) остатка на глубине хп
выражается как
∞ |
|
J (xn ,t) = ∫i(x,t) exp[−μ(x − xn )]dx, |
(3.25) |
xn
где i(x,t) – удельная радиоактивность снятого слоя, пропорцио-
нальная концентрации диффузанта C(x,t); μ – коэффициент поглощения излучения в веществе.
После преобразований из (3.25) получается
i(xn ,t) = μJn − |
∂Jn |
= |
const |
|
− |
x2 |
|
|
∂xn |
|
exp |
|
. |
(3.26) |
|||
πDt |
4D t |
|||||||
431

С учетом используемого излучения формула упрощается, и
D может быть определен вышеуказанным способом.
Верхний предел измеряемых коэффициентов диффузии соответствует величинам D* под точкой плавления и составляет
(10−8 ÷10−6 ) см2/ . сЕсли полагать, что различия в концентрациях при точном определении угла наклона прямой ln i(x,t) от x2 долж-
ны составлять не менее одного порядка, то нижний предел измеряемого коэффициента диффузии может быть оценен из соотноше-
ния x2 / 4D t 2,3 или x 3 D t .
D t .
Если считать, что минимальные толщины слоев при секционировании образца, доступные современным методам и имеющие физический смысл, достигают более микрона, а времена лабораторных отжигов для не очень короткоживущих радиоактивных изотопов могут достигать нескольких тысяч часов, то нижний предел коэффициента самодиффузии
D |
x2 |
|
10−10 см2 |
≈10−18 см2/с. |
|
9t |
104 3600 с |
||||
|
|
|
Решение для полубесконечных твердых тел. Исходное рас-
пределение концентрации создается контактом двух веществ (полубесконечных тел). Граничные условия (рис 3.74) имеют вид:
C(x,0) = 0 при x < 0 и C(x,0) = C0 при x > 0 .
Рис. 3.74. Начальное распределение концентраций для случая полубесконечных твердых тел
Представим себе, что область x > 0 содержит n участков толщиной α . Каждый участок вначале содержит C0 α растворенно-
го вещества, и если бы соседние участки были свободны, то распределение концентрации после диффузионного отжига имело вид (3.24). Действительное решение представляет собой суперпозицию
432
распределений для каждого из участков. Если αi – расстояние от x = 0 до центра i-го участка (рис. 3.75), то концентрация в точке x
в момент времени t |
описывается уравнением |
|
|
||||||
|
|
C |
0 |
n |
|
(x − α |
)2 |
|
|
C(x,t) = |
|
|
∑ |
αi exp − |
i |
|
. |
(3.27) |
|
|
πDt |
4Dt |
|
||||||
2 |
i=1 |
|
|
|
|
||||
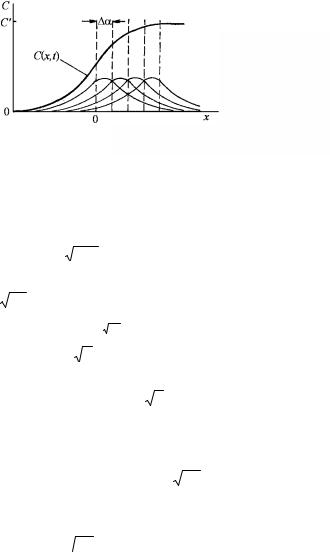
Рис. 3.75. Сумма экспонент, соответствующая решению для случая полубесконечных твердых тел
На рис. 3.75 показано, как сумма экспонент образует истинное распределение. В пределе при n → ∞ α → 0 и сумма в уравнении (3.15) переходит в интеграл:
|
|
C(x,t) = |
|
C0 |
|
|
|
|
∞ |
|
|
(x |
− α ) |
2 |
|
|
|
(3.28) |
|||
|
|
|
|
|
|
|
∫exp − |
|
|
|
d α. |
||||||||||
|
|
|
|
π |
|
|
|
|
|
4Dt |
|
||||||||||
|
|
2 |
|
Dt |
0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая |
x −α |
= η, получим |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
Dt |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
C |
|
2 |
|
Dt |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
∫exp(−η2 )dη. |
|
|
|
|
(3.29) |
|||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
erf(z) = |
|
2 |
z |
|
|
2 |
|
|
|||||
Поскольку |
функция, |
|
|
|
∫exp(−η |
|
)dη, |
называемая |
|||||||||||||
|
|
π |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
функцией ошибок или интегралом Гаусса, табулирована, ее можно использовать для преобразования решения
C(x,t) = |
C |
0 |
|
|
x |
|
|
1 |
− erf |
|
|
||
|
|
|
||||
|
2 |
|
2 |
Dt |
||
|
|
|||||
, (3.30)
вид которого праведен на рис. 3.75.
Каждое значение C / C0 в этом решении связано с определенным значением z = x / 2 Dt . Плоскость с любой постоянной кон-
Dt . Плоскость с любой постоянной кон-
433

центрацией (кроме C = C0 / 2 ) удаляется от плоскости x = 0 со скоростью, пропорциональной  Dt . Плоскости C = C0 / 2 соответствует z = 0, и она неподвижна.
Dt . Плоскости C = C0 / 2 соответствует z = 0, и она неподвижна.
Предположение о постоянстве D налагает ограничения на возможность использования решения этого типа для точного определения D . Решение с функцией ошибок применяют чаще всего в том случае, когда надо оценить количество вещества, находящегося в системе, для которой известно, что D изменяется вдоль диффузионной зоны (например, задача науглероживания или обезуглероживания стали). При этом для D получаются средние значения. В системе переменного химического состава, какой представляется диффузионная зона, D также обычно зависит от состава и для его определения необходимо применять метод Больцмана–Матано.
Решение Больцмана-Матано для коэффициента взаимной диффузии. Характерной особенностью взаимной диффузии являет-
~
ся зависимость ее коэффициента D от состава, т.е. от концентрации одного из компонентов бинарной системы. Это резко усложня-
~
ет определение D(C) из экспериментально получаемого концен-
трационного профиля (концентрационной кривой) в диффузионной зоне. Такое нахождение фактически есть обратная задача решения уравнения диффузии
∂C |
|
∂ |
~ |
∂C |
|
|
∂t |
= |
|
D |
|
(3.31) |
|
|
||||||
|
∂x |
|
∂x |
|
||
при начальных условиях (t = |
0): |
C = C′ при |
x < 0 , C = C′′ при |
|||
x > 0 ( x = 0 – начало координат принято в точке контакта исходной
диффузионной пары); при граничных условиях: C = C′ при x = −∞,
C = C′′ при x = +∞.
Аналитическое решение для C(x, t) при указанных начальных и граничных условиях известно. Однако для решения обратной зада-
~
чи оно мало что дает, так как D(C) входит в это выражение под
знаком интеграла.
Обратную задачу общепринято решать методом Больцмана– Матано. Используется подстановка Больцмана λ = x /  t . Тогда
t . Тогда
434
уравнение диффузии в частных производных преобразуется в обыкновенное дифференциальное уравнение:
|
|
|
|
|
|
λ dC |
|
|
d ~ dC |
|
|||
|
|
|
|
|
− |
2 dλ |
= |
|
|
D |
. |
(3.32) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dλ |
dλ |
|
||||
|
Из этого уравнения Матано формально получил соотношение |
||||||||||||
|
~ dC |
λ |
dC, |
интегрирование которого от C′ |
до C с учетом |
||||||||
d D |
= − |
2 |
|||||||||||
|
|
dλ |
|
|
|
|
|
|
|
|
|
|
|
граничного условия |
dC |
= 0 дает уравнение |
|
||||||||||
dλ C′ |
|
||||||||||||
|
|
|
|
|
~ |
dC |
|
|
= − |
1 C |
(3.33) |
||
|
|
|
|
|
D(C) |
dλ |
|
|
∫λdC . |
||||
|
|
|
|
|
|
|
C |
2 C′ |
|
||||
Аналогичное равноправное решение можно получить интегрированием от C′′ до C , т.е.
~ |
dC |
= − |
1 |
C |
(3.34) |
D(C) |
|
∫λdC . |
|||
|
dλ C |
|
2 C′′ |
|
|
Значит, должно выполняться дополнительное условие
C |
C |
C′′ |
|
∫λdC = ∫λdC или |
∫λdC . |
(3.35) |
|
C′ |
C′′ |
C′ |
|
Это условие выполняется только при специальном выборе начала отсчета по координатной оси λ . В исходной же системе координат эта точка на оси обозначается через λM , и из уравнения (3.35) получаем для ее определения уравнение:
C′′
∫(λ − λM )dC = 0,
C′
откуда
|
|
|
1 |
|
C ′′ |
(3.36) |
|||
|
λM = |
|
∫λdC, |
||||||
|
|
C′′−C′ |
|||||||
|
|
|
|
C ′ |
|
||||
и |
|
|
|
|
|
|
|
|
|
~ |
|
1 |
dλ |
|
C |
|
|||
D(C) = |
2 |
|
|
|
|
∫(λ − λM )dC |
(3.37) |
||
|
|||||||||
|
|
dC |
C C ′ |
|
|||||
или, возвращаясь к исходным переменным, имеем
435

~ |
1 |
dx |
C |
|
||
D(C) = |
|
|
|
|
∫(xM − x)dC . |
(3.38) |
|
|
|||||
|
2t dC C C ′ |
|
||||
Поскольку опыт дает C(x) при заданном времени отжига в виде экспериментальной кривой, то аналитическая аппроксимация C(x)
~
всегда будет приближенной, и Матано предложил вычислять D(C) графически. Производную определяют по наклону кривой в точке C , координату xM находят графически следующим образом (рис 3.76): площадь под кривой C(x) левее искомой координаты xM должна быть равна площади над кривой C(x) – правее. После нахождения xM графически вычисляется интеграл от C′ до C . Наи-
более трудоемкая операция – это, конечно, определение производной с достаточной точностью.
Рис. 3.76. Концентрационная кривая, используемая при расчете коэффициента взаимной диффузии
по методу Больцмана–Матано
Диффузия в однокомпонентных и бинарных cистемах. При рассмотрении уравнения диффузии (3.16) следует отметить, что члены Lii соответствуют обычным коэффициентам диффузии, а
недиагональные члены Lik (i ≠ k) вводятся для учета возможных
связей между различными диффузионными потоками и подчиняются соотношениям взаимности Онзагера (3.10). Их значение зависит от выбора плоскости, относительно которой измеряется Ji . Ес-
ли измерение проводится относительно плоскости, через которую поток атомов всех имеющихся веществ равен нулю, и если механизм диффузии вакансионный, то, следовательно:
436
n |
|
∑Ji = 0. |
(3.39) |
i =1
Так как каждому атому, перемещающемуся из одной плоскости решетки в другую, соответствует вакансия, движущаяся во встречном направлении, выражение (3.39) справедливо для плоскости, фиксированной относительно решетки, как и требуется для сопоставления Ji данного выражением (3.39), с формулами типа (3.16).
Вместе с соотношениями Онзагера выражение (3.39) позволяет уменьшить число независимых коэффициентов Lik. При подстановке уравнений типа (3.9) в (3.39), как следствие, получим
|
n |
|
n n |
∑Lik = 0 (i =1, 2,...n), |
|
k =1 |
(3.40) |
|
∑∑Lik xk = 0 |
n |
|
i =1 k =1 |
∑Lik = 0 (k =1, 2,...n). |
|
|
|
|
|
i =1 |
|
Формулы (3.40) образуют 2n соотношений. Однако не все из них
оказываются независимыми, потому что из обеих групп следует
n
∑Lik = 0. i,k =1
Спомощью одной из групп формул (3.36) можно исключить коэффициенты Lin (i =1, 2,... n) из выражения (3.9). Это дает (n–1) не-
зависимых соотношений: |
|
|
Ji ∑Lik (xk − xn ) (i |
= 1, 2, …, п – 1). |
(3.41) |
Теперь исключим коэффициенты |
Lnk (k =1, 2, ... n) |
из уравнения |
(3.9) с помощью нижней группы выражений (3.40). Тогда получим
n−1 |
|
Jn = −∑ Ji . |
(3.42) |
i−1
Это выражение показывает, что потоки не являются независимыми (3.35). После исключения (2n −1) коэффициентов Lin и Lni
остаются n2 −(2n −1) = (n −1)2 коэффициентов выражения (3.41).
На них соотношения (3.40) не накладывают никаких ограничений. В сочетании с выражением для скорости роста энтропии для п- компонентной системы имеется система из (2п – 1) соотношений,
437
из них |
1 |
(n −1)(n − 2) независимых соотношений Онзангера, так |
|
|
|
2 |
|
что |
1 n(n −1) коэффициентов оказываются независимыми. |
||
|
2 |
|
|
Наиболее простым примером является диффузия в чистом металле (самодиффузия). С учетом потока атомов и потока вакансий это двухкомпонентная система:
|
J1 = L11x1 + L12 x2 , |
(3.43) |
|
|
J2 = L21x1 + L22 x2 , |
||
|
|
||
где J1 – поток атомов; J2 – поток вакансий; J1 = −J2 . Из выраже- |
|||
ний (3.40) имеем |
|
|
|
L11 |
+ L12 = 0, L21 + L22 |
= 0, |
|
L11 |
+ L21 = 0, L12 + L22 |
= 0, |
|
так что из (3.41) и (3.42) получаем:
J1 = −J2 = L11 ( X1 − X 2 ) = −L12 ( X1 − X 2 ),
т.е. имеем один независимый коэффициент. Соотношения Онзагера очевидно, не имеют места, так как явление одиночное и эффекта наложения нет, а
σ= T −1(J1 X1 + J2 X 2 ) = T −1J1(X1 − X 2 ) .
Всистеме, содержащей атомы двух сортов, при постоянной
температуре возникают три потока: J1 и J2 – атомов сорта 1 и 2 и
J3 – вакансий.
В соответствии с соотношением (3 . 9) имеем:
J1 = L11 X1 + L12 X 2 + L13 X 3 , |
|
J2 = L21 X1 + L22 X 2 + L23 X 3 , |
(3.44а) |
J3 = L31 X1 + L32 X 2 + L33 X 3. |
|
Из (3.41) и (3.10): |
|
J1 = L11 (X1 − X3 ) + L12 (X 2 − X 3 ), |
|
J2 = L21 (X1 − X3 ) + L22 (X 2 − X 3 ), |
(3.44б) |
J3 = −(J 1 + J2 ). |
|
438
