ГЛАВА 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ

Современная кристаллография в широком смысле этого понятия включает в себя не только теорию симметрии кристаллов, но и методы структурной кристаллографии, изучение реальной структуры, образование и физические свойства кристаллов. Конкретные применения кристаллографических теорий и методов дают выход структурной кристаллографии в физику твердого тела, материаловедение, органическую химию, химию полимеров, молекулярную биологию, в изучение жидкостей и газов.

Курс физической кристаллографии предполагает рассмотрение не только кристаллографии и элементов симметрии в рамках теории твердого тела, но и структуры реальных моно и поликристаллов. Основная задача курса – научить студентов, занимающихся физическим материаловедением, кристаллографическому подходу при анализе результатов эксперимента.

1.1. Кристаллическое состояние

Кристаллами называют твердые тела, обладающие упорядоченной трехмерно-периодической пространственной атомной структурой [1]. Кристаллическое состояние есть термодинамически равновесное состояние твердого тела. Каждой твердой фазе фиксированного химического состава при данных термодинамических условиях соответствует одна определенная кристаллическая структура. Наличие естественных плоских граней у кристалла (огранение кристалла) является проявлением внутреннего атомного строения кристаллического вещества.

1.1.1. Основные законы кристаллографии

Основные законы кристаллографии были получены при изучении внешней огранки кристаллов, поэтому их иногда называют геометрическими или эмпирическими. Огранение кристаллов ха-

15

рактеризуется, прежде всего, наличием плоских граней. У кристаллов одного и того же вещества внешний облик или габитус, т.е. размеры, форма и даже число граней, может быть разным, но их можно так расположить в пространстве, что некоторые грани окажутся параллельными. Такие грани называются соответст-

венными.

Первый закон кристаллографии – закон постоянства углов был сформулирован датским ученым Н. Стеноном на примере двух веществ – кварца и гематита. Он гласит: углы между соответственными гранями кристаллов данного вещества постоянны и характерны для этого вещества.

Французский кристаллограф аббат Р.Ж. Гаюи нашел второй за-

кон кристаллографии – закон рациональных параметров. Если в качестве трех координатных осей кристалла выбрать некоторые его ребра, то отрезки, отсекаемые гранями на осях кристалла, относятся как целые числа. Таким образом, эти отрезки могут быть выражены как кратные некоторых осевых единиц. Наличие таких осевых единиц в трех направлениях приводит к выводу о трехмерной микропериодичности строения кристаллов. Из закона рациональных параметров и представлений об атомизме с необходимостью вытекает утверждение о трехмерно-периодическом атомном строении кристаллов.

Е.С. Федоров и А. Шенфлис теоретически доказали наличие 230 пространственных групп симметрии атомной структуры кристаллов. Однако первым прямым доказательством существования пространственной решетки стало явление дифракции рентгеновских лучей, открытое М. Лауэ, В. Фридрихом и П. Книппингом.

В кристаллографии и физике оказались важными группы, в которых три переменные остаются геометрическими координатами пространства, а четвертая имеет иной физический смысл. Такой переменной могут быть время или такие физические величины, как спин, знак заряда и т. п. Такого рода обобщения симметрии называют антисимметрией и цветной симметрией, а соответствующие группы – шубниковскими и беловскими, поскольку операцию антисимметрии предложил в 50-х годах прошлого века А. В. Шубников, а цветные группы – Н. В. Белов.

16

1.1.2. Макроскопические и микроскопические характеристики кристаллов

Наиболее общими макроскопическими свойствами кристалличе-

ского вещества являются однородность, анизотропия и симметрия.

Понятие макроскопической однородности означает, что в любых участках кристаллического вещества все свойства его тождественны. Интересующее нас свойство кристалла F может быть скалярным (например, теплоемкость, плотность), векторным (например, поляризация) или в общем случае тензорным (например, упругость). Понятие кристаллической однородности означает независимость любого свойства F при переходе от измерения в точке x (x1, x2, x3) к любой другой точке x + x ′ (x1 + x′1, x2 + x′2, x3 + x′3):

Другими словами, однородность есть инвариантность свойств относительно произвольного переноса начала координат в кристаллическом веществе.

Понятие макроскопической однородности позволяет рассматривать кристаллическое вещество как непрерывное, как однородную непрерывную среду. Такой подход чрезвычайно важен в кристаллографии, так как позволяет давать феноменологическое описание многих физических свойств кристаллов без использования представлений об их дискретном атомном строении.

Не только кристаллы, но и жидкости, аморфные тела и газы обладают свойством макроскопической однородности. Специфичность кристаллического вещества и отличие его от других состояний проявляется при рассмотрении его анизотропии.

Если в соответствии с принципом макроскопической однородности можно отнести свойство F к произвольной точке, то анизотропию можно описать как ориентационную зависимость свойства F, т. е. зависимость его от направления n, вдоль которого опреде-

Анизотропия свойственна не только кристаллам. Она сохраняется в кристаллических текстурах, присуща жидким кристаллам, природным и синтетическим полимерным веществам. Анизотропия

17

этих веществ, как и кристаллов, в основном определяется их атомным строением и не обязательно требует различия всех свойств во всех направлениях. Наоборот, допустимо закономерное равенство F для некоторых разных направлений. Такое равенство есть не что иное, как проявление симметрии кристаллов.

Симметрию физического свойства F можно представить в виде:

F (x) = F (x ′) = … = F (x (n)), (1.3)

т.е. функция F симметрична, если она инвариантна относительно определенного закона преобразования аргументов.

С точки зрения симметрии, можно сформулировать понятие кристаллической однородности и анизотропии. Однородность – независимость свойств кристаллического вещества от выбора точки измерения – с позиций симметрии является инвариантностью по отношению к произвольному, параллельному себе его переносу. Анизотропия же кристаллов – зависимость свойств от направлений

– сама проявляется в рамках симметрии: функции, описывающие свойства, сами являются симметричными.

Таким образом, кристаллическое вещество по своим макроскопическим признакам можно определить как однородную анизотропную симметричную среду.

1.1.3. Решетка и структура кристаллов

Рассмотрим более подробно закономерности внутреннего строения кристаллов. Конкретное расположение атомов в кристалле называют структурой вещества. Всякое кристаллическое вещество может быть разбито на тождественные участки (ячейки), содержащие один или несколько определенным образом расположенных в них атомов. Бесконечно протяженное расположение атомов, состоящее из периодически повторяющихся одинаковых яче-

ек, называют кристаллическим пространством. Преобразованием симметрии называют операцию, переводя-

щую точки кристаллического пространства в новое положение без изменения расстояний между всеми его точками. Две точки кристаллического пространства O и O′ являются гомологичными (эквивалентными), если существует такое преобразование симметрии,

18

переводящее O в O', после которого кристаллическое пространство нельзя отличить от исходного ни в отношении свойств, ни в отношении геометрии расположения его точек.

Математически кристаллическое пространство строят на следующих постулатах.

1.Не все точки кристаллического пространства одинаковы (в любом смысле).

2.Кристаллическое пространство однородно, т.е. существует шар такого постоянного радиуса R (шар однородности), что где бы

его ни выбрать, внутри него найдется точка x ′, симметрично равная любой наперед заданной точке пространства x.

3. В пространстве есть такие точки (по крайней мере, одна точка x), что вокруг них в шаре радиуса r (шар дискретности) нет ни одной симметрично равной им точки.

Указанные постулаты достаточны для построения всей геометрической кристаллографии и вывода многих геометрических свойств кристаллического вещества.

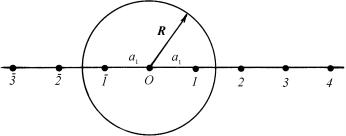
Выберем любую точку кристаллического пространства, например точку О (рис. 1.1).

Рис. 1.1. Узловой ряд

Опишем вокруг нее шар однородности с радиусом R с центром в данной точке. Из рентгеновских данных установлено, что значение R не превышает 5 нм. Внутри шара однородности обязательно должна найтись хотя бы одна точка, гомологичная ранее заданной. Если этих точек несколько, то выберем из них ближайшую (точка 1), находящуюся от выбранной точки на расстоянии a1. Проведем через точки О и 1 прямую. Точка 1 гомологична точке О и, следовательно, ничем не отличается ни по геометрическим, ни по физи-

19

ческим свойствам. Так как точка О имеет соседом справа точку 1, то точка 1 должна иметь на том же расстоянии гомологичную точку 2 и т.д. Таким образом, получаем ряд гомологичных точек, простирающихся бесконечно вправо от точки О. Аналогично рассуждая, что точка 1 имеет слева соседнюю гомологичную точку О,

приходим к выводу, точка О должна иметь соседом слева точку 1,

расположенную от нее вдоль прямой на расстоянии a1, точка 1 –

соседом точку 2 . В результате получаем бесконечный ряд гомологичных точек, называемый узловым рядом. Узловой ряд характеризуется кратчайшим расстоянием между гомологичными точками (узлами) a1, называемым длиной трансляции. Таким образом, трансляция является преобразованием симметрии, свойственным бесконечному кристаллическому пространству.

Проведя рассуждения, аналогичные сделанным выше, можно показать, что гомологичные точки кристаллического пространства образуют пространственную решетку.

Различие между структурой и пространственной решеткой можно проиллюстрировать на примере одномерной атомной структуры, содержащей атомы трех сортов (рис. 1.2).

Рис. 1.2. Одномерная атомная структура (а) и отвечающий ей узловой ряд (б)

Поместив любой узел, отвечающий этой структуре, в центр атома сорта A, обнаружим остальные узлы в центрах атомов того же сорта. Если поместить узел в точку, делящую пополам расстояние между атомами сорта A и B, то обнаружим остальные узлы в гомологичных точках кристаллического пространства.

Таким образом, структура кристалла, будучи физической реальностью, состоит из атомов, а пространственная решетка как способ

20