
- •от ХХ УУУУ 20007 г. МГУП
- •Учебник подготовлен в рамках Инновационной образовательной программы
- •ISBN 978-5-7262-0821-3
- •ISBN 978-5-7262-0822-0 (т.1)
- •Глава 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
- •Предисловие к тому 1
- •Глава 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
- •1.1. Кристаллическое состояние
- •1.1.3. Решетка и структура кристаллов
- •1.2. Основы кристаллографии
- •1.2.1. Кристаллографические проекции
- •1.2.2. Пространственная решетка
- •1.2.3. Кристаллографические символы
- •1.2.4. Обратная решетка
- •1.2.5. Матрица ортогонального преобразования
- •1.2.6. Преобразование индексов направлений
- •1.3. Симметрия кристаллов
- •1.3.1. Поворотные оси симметрии
- •1.3.2. Инверсионные оси
- •1.3.3. Зеркально-поворотные оси
- •1.3.4. Элементы теории групп
- •1.3.5. Точечные группы симметрии
- •Бравэ
- •Бравэ
- •Распределение ячеек Бравэ по сингониям показано в табл. 1.4.
- •1.3.6. Пространственные группы
- •1.3.7. Предельные группы симметрии
- •1.4. Структура кристаллов
- •1.4.1. Плотнейшие упаковки в структурах
- •1.4.3. Структурные типы соединений типа АВ
- •1.4.4. Структурные типы соединений типа АВ2
- •1.4.5. Структурные типы соединений типа АmВnCk
- •1.4.7. Структура фуллеренов, фуллеритов
- •1.4.8. Структура поверхности
- •1.5. Физические свойства кристаллов
- •1.5.1. Принцип симметрии в кристаллофизике
- •1.5.4. Упругие свойства кристаллов
- •1.6. Кристаллография пластической деформации
- •1.6.1. Геометрия пластической деформации
- •1.6.2. Кристаллографическая текстура
- •1.7. Кристаллография границ зерен
- •1.7.1. Малоугловые границы
- •1.7.2. Высокоугловые границы
- •1.8. Кристаллография мартенситных превращений
- •1.8.1. Морфология мартенситных превращений
- •1.8.2. Кристаллография мартенситных превращений
- •Контрольные вопросы, задачи и упражнения
- •Глава 2. ДЕФЕКТЫ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ
- •2.1. Точечные дефекты
- •2.1.1. Вакансии и межузельные атомы
- •2.1.2. Энергия образования точечных дефектов
- •Контрольные вопросы
- •Список использованной литературы
- •Глава 3. ФИЗИКА ТВЕРДОГО ТЕЛА
- •3.1. Строение атомов и межатомные взаимодействия
- •3.1.1. Классификация конденсированных систем
- •3.1.4. Энергия связи кристаллов
- •3.1.5. Типы связи в твердых телах
- •Металлическая связь. В отличие от ковалентной связи, которая образуется между двумя соседними атомами в результате коллективизации двух валентных электронов, металлическая связь появляется вследствие коллективизации всех валентных электронов. Эти электроны не локализуются у отдельных атомов, а принадлежат всему коллективу атомов. Поэтому они называются свободными электронами, перемещающимися по всему объему металла и в каждый момент времени равномерно распределенными в нем. Классическим подтверждением наличия таких свободных электронов в металлах является опыт Мандельштама и Папалекси, когда при резкой остановке вращающейся катушки, сделанной из металлической проволоки, в ней возникал электрический ток. Ярким подтверждением этому являются высокие электро- и теплопроводность металлов.
- •Ионная связь. Атомы, стоящие в периодической системе Д. И. Менделеева рядом с инертными газами, обладают склонностью принимать их конфигурацию либо путем отдачи, либо путем принятия электронов. У атомов щелочных металлов, стоящих непосредственно за инертными газами, валентный электрон слабо связан с ядром, так как движется вне заполненного слоя. Поэтому этот электрон может быть легко удален от атома. У галоидов, стоящих непосредственно перед инертными газами, недостает одного электрона для заполнения устойчивого слоя благородного газа. Поэтому галоиды обладают высоким сродством к дополнительному электрону.
- •Изоморфизм и морфотропия. Рассмотрим несколько ионных соединений щелочных металлов с галоидом бромом: LiBr, NaBr, KBr, RbBr и CsBr. Первые четыре соединения имеют решетку типа NaCl, а пятое соединение CsBr кристаллизуется в решетке типа CsCl.
- •3.2. Основы электронной теории кристаллов
- •3.2.1. Квантовая теория свободных электронов
- •3.2.2. Зонная теория металлов
- •3.3. Теория фаз в сплавах
- •3.3.1. Классификация фаз в сплавах
- •3.3.2. Твердые растворы
- •3.3.3. Промежуточные фазы
- •1B3.4. Диффузия и кинетика фазовых превращений
- •2Bв металлах и сплавах
- •4B3.4.1. Линейные феноменологические законы
- •5B3.4.2. Макроскопическое описание явления диффузии
- •6B3.4.3. Атомная теория диффузии в металлах
- •9B3.4.5. Диффузия и фазовые превращения в металлах
- •10Bи сплавах
- •3B3.5. Электрические свойства твердых тел
- •11B3.5.1. Основы электронной теории электропроводности
- •14B3.5.3. Эффект Холла
- •15B3.5.4. Связь электросопротивления со строением сплавов
- •20B3.5.7. Сверхпроводимость
- •3.6. Магнитные свойства твердых тел
- •3.6.1. Основные определения. Классификация веществ по магнитным свойствам
- •3.6.2. Магнитные свойства свободных атомов
- •3.6.3. Физическая природа диамагнетизма
- •3.6.4. Физическая природа парамагнетизма
- •3.6.5. Магнитная восприимчивость слабых магнетиков
- •3.6.6. Основы теории магнитного упорядочения
- •3.6.7. Доменная структура ферромагнетиков
- •3.6.8. Магнитные свойства ферромагнетиков
- •3.6.9. Антиферромагнетики и ферримагнетики
- •3.7. Тепловые свойства твердых тел
- •3.7.2. Теплоемкость кристаллических твердых тел
- •3.7.3. Теплопроводность твердых тел
- •3.7.4. Термическое расширение твердых тел
- •3.8. Упругие свойства твердых тел
- •3.8.1. Основные характеристики упругости
- •3.8.2. Упругость чистых металлов и сплавов
- •3.8.3. Ферромагнитная аномалия упругости
- •3.8.5. Внутреннее трение
- •Контрольные вопросы
- •Список использованной литературы
шаются. Такое изменение температур плавления и кипения связано с тем, что при переходе от неона к ксенону растет общее число электронов на оболочках этих элементов и, следовательно, большее количество электронов может участвовать в создании дисперсионных сил притяжения.
В кристаллах, связанных силами Ван-дер-Ваальса, направленности и насыщаемости связей нет. Поэтому с помощью связи этого типа образуются кристаллы с плотнейшими ГЦК и ГПУ решетками, так как в этом случае энергия системы тем меньше, чем ближе атомы друг к другу.
Например, неон и аргон кристаллизуются в ГЦК структуру, насыщенная молекула азота N2 – в ГПУ, молекулы CH4 – в ГЦК.
3.2. Основы электронной теории кристаллов
Электронная теория кристаллических твердых тел изначально разрабатывалась применительно к металлам. Металлы занимают особое положение в физике твердого тела, обнаруживая ряд отличительных свойств, отсутствующих у других твердых тел. Металлы обладают высокой тепло- и электропроводностью, уникальными термоэлектрическими и гальваномагнитными свойствами, сильным парамагнетизмом и ферромагнетизмом, ковкостью и пластичностью, металлическим блеском и непрозрачностью. Необходимость объяснения подобных свойств металлов стимулировала создание современной электронной теории твердого тела. Для объяснения свойств неметаллических твердых тел было необходимо понять свойства металлов.
С начала прошлого века физики пытаются построить простые модели металлического состояния, которые позволили бы качественно и даже количественно объяснить характерные металлические свойства. Интерпретация свойств металлов, основанная на модели свободных электронов, была развита задолго до создания квантовой механики Друде (см. п. 3.5.1). На этом пути классическая теория имела ряд выдающихся успехов и одновременно несколько серьезных провалов. К успехам относился вывод закона Ома и соотношения Видемана–Франца (см. п. 3.7.3). В то же время класси-
371
ческая теория оказалась полностью неспособной объяснить температурное поведение теплоемкости и парамагнитной восприимчивости электронов проводимости. Кроме того, модель Друде приводила к ряду концептуальных трудностей, что и определило круг вопросов, с которыми теории металлов пришлось иметь дело в последующий период развития. Требовалось ответить на вопросы, почему конденсированная среда «прозрачна» для электронов проводимости и почему электроны проводимости ведут себя в этом отношении как газ невзаимодействующих частиц. Они нашли свое разрешение лишь после создания квантовой теории твердого тела. В последующих разделах кратко рассматриваются основные положения современных квантовых моделей теории свободных электронов (Зоммерфельд) и зонной теории (Блох-Бриллюэн).
3.2.1.Квантовая теория свободных электронов
Вквантовой теории свободных электронов не учитывается структура металла и предполагается, что металл содержит некоторое число делокализованных валентных электронов, движущихся свободно, как будто они являются частицами электронного газа. Электростатическое отталкивание между электронами также не учитывается (так называемое приближение независимых электронов): делается допущение, что металл содержит равномерно распределенный положительный заряд, нейтрализующий заряд электронов. Конечно, такое допущение является чрезмерным упрощением задачи, поэтому теория дает удовлетворительные результаты только для щелочных металлов. Для остальных металлов она не дает хороших результатов, однако используется при их изучении благодаря сравнительно простой математической трактовке
ивозможности легко получить основу, облегчающую рассмотрение более сложных теорий.
Модель свободных электронов, учитывая, что положительный заряд в металле распределен с равномерной плотностью, предполагает поле с постоянным положительным потенциалом W, а следовательно, и постоянной потенциальной энергией U = −eW . Эта
энергия резко возрастает у поверхности металла и тем самым пре-
372
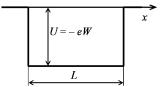
пятствует выходу электронов наружу. Такая модель позволяет рассматривать металл как потенциальный ящик (рис. 3.41).
Рис. 3.41. Энергетическая модель металла (U0 – скачок потенциальной энергии у поверхности металла, L – размер куска (обычно в форме куба)
металла)
Сопоставление с экспериментальными данными показывает, что для большинства металлов U порядка 10 эВ. Вне металла, как это ясно из схемы, потенциальная энергия электронов принимается равной нулю. Поэтому энергия электрона в металле E = –U + mυ2/2,
так как кинетическая энергия свободного электрона равна mυ2/2,
где υ – его скорость.
Для многих целей в выражении для полной энергии электрона E не обязательно учитывать постоянный член U, и свободному электрону, находящемуся в металле, приписывается нулевое значение потенциальной энергии. В этом случае за полную энергию электрона принимается чисто кинетическая энергия.
Одним из наиболее замечательных выводов теории свободных электронов является то, что она простейшим образом показывает различие между «электронным газом» при плотностях, соответствующих существованию электронов в твердых телах, и обычным молекулярным газом, подчиняющимся законам классической статистики Максвелла–Больцмана. Это отличие связано с тем, что электронный газ подчиняется не классической, а квантовой ста-
тистике Ферми–Дирака, характерной для частиц с нецелочисленным спином.
В квантовой статистике Ферми-Дирака шестимерное фазовое пространство и пространство импульсов также применяются, но при этом учитываются ограничения, налагаемые принципом неоп-
ределенности Гейзенберга и принципом запрета Паули.
Электроны, образующие газ свободных электронов, обладают волновыми свойствами, и их движение описывается волновым уравнением Шредингера. Следствием этого является то, что энергия электрона в твердом теле становится квантованной, т.е. может
373
принимать лишь строго определенные значения. Каждое такое значение соответствует определенному квантовому состоянию электрона в твердом теле.
Действительно, если в предположении свободных электронов в металле положить потенциал металла W равным нулю, то уравнение Шредингера для свободного электрона в случае одномерного потенциального ящика можно записать в виде
−(h2 / 2m)(d2Ψ / dx2 ) = EΨ. |
(3.1) |
Так как электрон не может свободно покидать металл, то волновая функция на его границах в точках x = 0 и x = L должна обращаться в нульΨ(0) = Ψ(L) = 0. Уравнению Шредингера при та-
ких граничных условиях отвечает набор функций типа стоячих волн Ψn (x) = Asin(2πx / λn ), где длина волны λn такова, что на от-
резке L укладывается целое число n полуволн, т.е. λnn / 2 = L , тогда
|
|
|
|
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ψn (x) = Asin |
|
|
x . Подставим это выражение в уравнение Шре- |
||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дингера (3.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
h2 |
|
d2Ψ |
|
h2 |
|
|
πn 2 |
|
πn |
|
πn |
|
|
|||||||||
− |
|
|
|
n |
= − |
|
|
− A |
|
|
|
|
sin |
|
x |
= En Asin |
|
x . |
(3.2) |
||||
2m |
|
dx |
2 |
2m |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
L |
|
|
L |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда следует |
|
En = |
h2 |
|
|
(πn) |
2 |
. Таким образом, энергия электрона |
|||||||||||||||
|
2m |
|
|
L2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
не представляется непрерывной функцией, а может принимать лишь определенные значения, называемые собственными, и поэтому энергетический спектр свободных электронов в металле яв-
ляется дискретным.
Наличие у электрона волновых свойств вследствие принципа неопределенности Гейзенберга исключает возможность различить
состояние (x, y, z, px, py, pz) |
и состояние (x + dx, y + dy, z + dz, |
px + dpx , py + dpy , pz + dpz ) , |
если произведение dxdydzdpxdpydpz |
оказывается меньше h3. Принцип неопределенности утверждает, что можно различить два состояния, если dxdydzdpxdpydpz ≥ h3 . Так как произведение dxdydzdpxdpydpz представляет элемент шес-
374
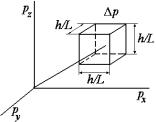
тимерного фазового пространства, то из соотношения неопределенностей следует, что различным элементам фазового пространства будут соответствовать различные состояния электрона только в том случае, если размер этих элементов не меньше h3. Поэтому в квантовой статистике за элементарную ячейку 6-мерного фазового пространства принимается предельно минимальный объем, равный h3. Для одного направления, например, вдоль оси x, в предельном случае можно записать dxdpx = h или x px = h. Отсюда px = h / x .
В теории свободных электронов, как об этом было сказано выше, используется представление об электронах в потенциальном ящике, причем в реальном пространстве металл берется в виде куба с длиной ребра L. В этой теории нет необходимости определять любую из трех координат каждого электрона в реальном пространстве точнее, чем L. Поэтому, полагая x = y = z = L , размеры
энергетических ячеек в пространстве импульсов по различным координатным осям будут определяться как px = h / L ; py = h / L
и pz = h / L . Таким образом, объем каждой ячейки, характери-
зующей отдельное электронное состояние в пространстве им-
пульсов, равен px py pz = h3/V, где V = L3 (рис. 3.42).
В соответствии с принципом Паули в каждой элементарной ячейке h3/V пространства импульсов, мо-
жет находиться только два электрона с противоположными спинами. Поэтому общий объем в том же пространстве импульсов, который занимают N свободных электронов, равен (N/2)(h3/V). Этот объем электронный газ занимает при абсолютном нуле температуры. Напомним, что все импульсы молекул идеального газа в классической статистике при абсолютном нуле равны нулю.
Объем (N/2)(h3/V) в пространстве импульсов будет соответствовать минимуму энергии системы в том случае, когда его форма будет сферой. Такую сферу называют сферой Ферми (рис. 3.43).
375
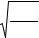
Радиус этой сферы pF определяется из равенства
4πpF3 / 3 = Nh3 / 2V , откуда
pF = h3 83πNV .
Если объем h3 /V каждой энергетической ячейки, из совокупности которых состоит сфера Ферми, зависит от общего объема металла, то радиус сферы Ферми от объема не зависит, так как в формулу для pF входит удельный объем, приходящийся на один атом – V/N.
Уравнение Шредингера для свободного электрона, находящегося в трехмерном потенциальном ящике (кубе с ребрами длиной L) и бесконечно высокими барьерами на его стенках, имеет вид
ΔΨ + |
8π2m |
EΨ = 0 . |
(3.3) |
|
h2 |
||||
|
|
|
Если граничные условия записать в виде Ψх(–L/2) = Ψх(L/2) = 0,
Ψу(–L/2) = Ψу(L/2) = 0, Ψz(–L/2) = Ψz(L/2) = 0, то обобщая волновую функцию, полученную ранее для одномерного случая, на трехмерный случай, получим волновую функцию в виде стоячей волны
πn |
|
πny |
|
πn |
|
|||
Ψ(r) = Asin |
|
x x sin |
|
y sin |
|
z z . |
||
|
|
|
||||||
|
L |
|
|
L |
|
|
L |
|
|
|
|||||||
При рассмотрении кристаллов чаще вместо указанных гранич-
ных условий вводят периодические граничные |
условия |
Ψ(x, y, z) = Ψ(x + L, y, z) = Ψ(x, y + L, z) = Ψ(x, y, z + L) . |
При та- |
ких граничных условиях волновая функция выбирается в виде плоской бегущей волны Ψk (r) = Aexp(ikr) , где k – волновой вектор.
Подставляя выражение для Ψk (r) в граничные условия, получим
Aexp[i(kx x + kx L + ky y + kz z)]= Aexp[i(kx x + ky y +k yL + kz z)]= = Aexp[i(kx x + ky y + kz z + kz L)]= Aexp[i(kx x + ky y + kz z)]
Отсюда вытекает, что exp(ikx L) = exp(iky L) = exp(ikzl) =1. Учитывая, что exp(z) =1 только в том случае, когда z = 2πni , где n – целое число, находим, что компоненты волнового вектора k должны иметь вид
376

kx = 0, ± 2πnx / L; ky = 0, ± 2πny / L; kz = 0; ± 2πnz / L ,
где nx ,ny ,nz – целые положительные или отрицательные числа,
или ноль. Из этого условия следует, что на каждые два состояния, отвечающие двум электронам с противоположными спинами, при-
ходится объем (2π/L)3 =8π3 /V , где V = L3 - объём металла.
Если принять, как об этом говорилось ранее, потенциальную энергию свободных электронов в металле равной нулю, то полная энергия каждого электрона будет равна кинетической и составит
E = |
mυ2 |
= |
p2 |
. |
|
2 |
2m |
||||
|
|
|
|||
Так как объем энергетической ячейки |
h3 /V оказывается конеч- |
||||
ным, то свободные электроны, относящиеся в пространстве импульсов к окрестностям начала координат, не могут иметь нулевую энергию, а максимальная энергия электронов, соответствующая поверхности сферы Ферми – энергия Ферми – определяется из выражения
|
P2 |
|
h2 |
3N |
2 / 3 |
|
||
EF = |
F |
= |
|
|
|
|
. |
(3.4) |
2m |
|
|
||||||
|
|
2m |
8πV |
|
|
|||
Обычно берут в качестве N число Авогадро NA, вместо V подставляют объем 1 моля металла Va, определяемого по формуле Va = A / ρ, где A – атомная масса, а ρ – плотность. Тогда по формуле
для EF можно расчетным путем определить энергию Ферми одновалентных металлов (табл. 3.11)
|
|
|
|
|
|
|
Таблица 3.11 |
||
|
|
Энергия Ферми одновалентных металлов |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Эле- |
Li |
Na |
K |
Rb |
Cs |
Cu |
Ag |
Au |
|
мент |
|
||||||||
|
|
|
|
|
|
|
|
|
|
EF, эВ |
4,74 |
3,16 |
2,06 |
1,79 |
1,53 |
7,10 |
5,52 |
5,56 |
|
Расчет энергии Ферми для двух- и трехвалентных металлов можно провести таким же путем, только число Авогадро необходимо умножать соответственно на 2 или 3 (табл. 3.12).
377
Таблица 3.12
Энергия Ферми двух- и трехвалентных металлов
Эле- |
Be |
Mg |
Ca |
Zn |
Cd |
Al |
Ga |
In |
|
мент |
|||||||||
|
|
|
|
|
|
|
|
||
EF, эВ |
14,14 |
7,13 |
4,68 |
9,39 |
7,46 |
11,63 |
10,35 |
8,60 |
Сравнение значений EF, рассчитанных по теории свободных электронов, с экспериментально наблюдаемой шириной полос испускания металлов, полученных при исследовании спектров металлов в мягких рентгеновских лучах, показывает довольно хорошее согласование теоретических и экспериментальных данных.
Само собой разумеется, что по экспериментальным значениям ширины полосы испускания мягких рентгеновских лучей можно производить обратный подсчет количества электронов от каждого атома, являющихся свободными. Если в формуле для EF вместо энергии Ферми подставить ширину полосы испускания E , а число свободных электронов обозначить в виде произведения nc·NA, где nc – число свободных электронов от каждого атома, то
|
h |
2 |
|
|
3 / 2 |
|
E = |
|
|
3nc NA |
|
||
|
|
8πV |
|
, |
||
2m |
||||||
|
|
|
|
a |
|
|
n = 8π(2m)3/ 2 |
E3/ 2 = 3,8 103/ 2 E3/ 2 |
A |
. |
|
|
||||
c |
3Nh3 |
|
ρ |
|
|
|
|||
Здесь E подставляется в эргах.
Теория свободных электронов позволяет легко получить аналитические выражения для плотностей распределения по энергиям
электронных состояний N(E) и электронов n(E). Из определения,
что n(E)dE равно числу электронов, приходящихся на единицу объема, в полосе энергетического спектра, ограниченного энергиями E
EF
и E+dE, следует, что ∫n(E)dE = N , т.е. общему числу свободных
0 |
|
EF |
|
электронов в металле; одновременно ∫ |
N(E)dE = N / 2 . Отсюда |
0 |
|
n(E) = dN/dE , а N (E) = d(N/2)/dE . |
|
378 |
|

При этом N определяется из уравнения для энергии E при V = 1
N = (8π/3h3 )(2m)3 / 2 E3 / 2 . Тогда
n(E) = (4π/h3 )(2m)3 / 2 |
E , |
|
N (E) = (2π/h3 )(2m)3 / 2 |
E . |
(3.5) |
Из этих выражений следует, что N(E) так же, как и n(E), имеют параболическую зависимость от энергии E (рис. 3.44).
Средняя энергия одного электрона рав-
на отношению энергии всех электронов к их полному числу:
Рис. 3.43. Вид сферы Ферми в пространстве импульсов
|
EF |
|
EF |
E3 / 2dE |
|
|
|
|
|
|
|
|
|
|
|||
|
∫ |
En(E)dE |
|
∫ |
|
2 |
|
E |
5 / 2 |
|
|
|
|||||
Eср = |
0 |
|
= |
0 |
|
|
|
= |
5 |
|
F |
= |
3 |
EF . |
|||
|
|
|
|
|
|
||||||||||||
EF |
EF |
|
|
|
|
|
|
|
|
||||||||
|
|
E |
1/ 2 |
dE |
|
|
2 |
|
EF3 / 2 |
5 |
|
||||||
|
|
3 |
|
|
|
|
|||||||||||
|
|
∫n(E)dE |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим теперь распределение электронов по энергиям с повышением температуры от абсолютного нуля. Это распределение задается функцией распределения статистики Ферми–Дирака:
1 |
|
|
f = |
|
, |
exp[(E −μ)/ kT ]+1 |
||
где μ – химический потенциал.
Функция распределения выражает вероятность заполнения электронами энергетических ячеек объемом h3/V в пространстве импульсов. Так, ячейки, для которых f = ½, заполнены в среднем наполовину, ячейки, для которых f = 1, заполнены целиком (двумя электронами с противоположными спинами) и т.д.
При абсолютном нуле температуры химический потенциал μ=EF |
|
и выражение для f принимает вид: f =1/ |
([exp(E − EF )/ kT ]+1). |
Тогда при E ≤ EF f = 1, а при E > EF |
f = 0. При этом электрон- |
ный газ находится в полностью вырожденном состоянии.
На практике, как известно, имеют дело с температурами в сотни и тысячи градусов Кельвина. С повышением температуры электроны подвергаются тепловому возбуждению, кинетическая энергия электронного газа увеличивается. Однако не все электроны могут
379

при этом повышать свою энергию. В самом деле, при реальных температурах, к примеру при 1000 К, величина энергии теплового возбуждения kТ оказывается на два порядка меньше энергии Ферми (kT ~ 0,1 эВ; EF ~ 10 эВ). Поэтому повышать свою энергию могут только те электроны, которые находятся вблизи энергии Ферми
(E ≥ EF – kT).
Электроны, энергия которых ниже этих значений, должны были бы переходить в энергетические ячейки, уже полностью заполненные двумя электронами с противоположными спинами, что невозможно в силу действия принципа запрета Паули.
В общем виде при любой температуре химический потенциал
выражается через энергию Ферми следующим образом: |
|
|||||||||||||||
|
μ = EF |
− |
|
|
π |
|
k2T 2 |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
12 EF |
|
|
|
|
|
|
|
||||||
Тогда функция распределения приобретает вид: |
|
|
|
|||||||||||||
f = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
. |
(3.6) |
|
|
|
2 |
2 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
π |
|
|
|
k T |
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
+1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
exp E − EF + |
12 |
|
|
EF |
|
|
|
||||||||
|
|
|
|
kT |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График температурной зависимости функции распределения представлен на рис. 3.45. Масштаб графика по оси абсцисс не соблюден, так как kT/EF ~ 0,01 для обычных температур.
|
|
Рис. 3.44. Зависимость плотности |
Рис. 3.45. Распределение |
состояний электронов от энергии |
Ферми–Дирака |
Снятие вырождения с электронного газа будет происходить при десятках тысяч градусов, когда будет достигнуто равенство kT =EF. Однако тогда все металлы будут находиться в газообразном состоянии. При E = EF с учетом того, что kT/EF ~ 0,01, f = 1/2. Из рис. 3.45
380
