Теперь в соответствии с (1.141)

ni = 18 (6·1·1 + 2·1·3 + 6·1·1 + 2·1·3) = 3.

Таким образом, тензор, описывающий физическое свойство, заданное симметричным тензором второго ранга кристалла ромбической сингонии mmm (D2h), например, электропроводность монокристалла α-U, имеет 3 независимых компонента.

1.6. Кристаллография пластической деформации

Под действием механического напряжения кристаллы деформируются. При малых напряжениях кристалл деформируется упруго, а после разгрузки его начальная форма полностью восстанавливается. В области упругости связь между деформацией и напряжением подчиняется закону Гука. Предел упругости связан с предельным напряжением, до которого выполняется закон Гука. Практически предел упругости неотличим от напряжений, при котором появляется остаточная деформация, т.е. так называемого предела текучести. Если нагрузить кристалл больше предела текучести, а затем разгрузить, то его прежняя форма не восстанавливается, кристалл остается пластически деформированным.

1.6.1.Геометрия пластической деформации

вмонокристаллах

Пластическая деформация монокристалла может происходить путем скольжения или путем двойникования.

Основным способом пластической деформации кристаллов при нормальных и низких температурах является скольжение. Оно представляет собой перемещение одной части кристалла относительно другой без изменения объема кристалла. Обычно скольжение осуществляется по определенным кристаллографическим плоскостям

122

вдоль определенных кристаллографических направлений в зависимости от структуры кристалла. Смещение частей кристалла при скольжении происходит на величину, кратную вектору трансляции кристаллической решетки в направлении скольжения. Поэтому скольжение часто называют трансляционным скольжением.

Механическое двойникование − это деформация, в результате которой две части кристалла оказываются в положениях зеркальносимметричных или повернутых относительно оси второго порядка.

При пластической деформации скольжением выполняется закон критического скалывающего напряжения (закон Шмида), который заключается в том, что деформация начинается лишь тогда, когда внешнее напряжение впервые достигает величины критического скалывающего напряжения по одной из систем скольжения.

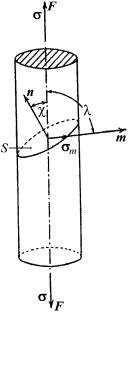
Рассмотрим монокристалл в форме цилиндра, который растягивается под действием нормального напряжения σ вдоль направления F (рис. 1.75).

На плоскость скольжения S c нормалью n действует напряжение σcosχ, а компонента σm его в направлении скольжения m равна σm = σcosχcosλ, где λ − угол между направлением скольжения и осью растяжения. Скольжение начнется лишь в условиях, когда критическое скалывающее напряжение σm достигнет значения, равного пределу текучести. Множитель cosχcosλ

называют ориентационным множителем или фактором Шмида.

~

где h − матрица-строка, компонентами которой являются направ-

ляющие косинусы нормали к плоскости скольжения, а m − матрицастолбец с направляющими косинусами направления скольжения.

123

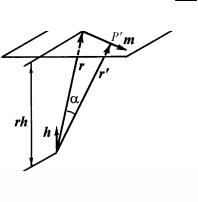
Тензор пластической деформации. В результате скольжения происходит сдвиговая деформация. Если точка P, находящаяся на расстоянии r от начала координат O, движется в плоскости скольжения с единичным вектором нормали h в направлении скольжения с единичным вектором m, то новое положение точки P − точка P' будет находиться от точки O на расстоянии r' (рис. 1.76). Тогда

где α − величина сдвига (смещение точки P). Если α мало, то по аналогии с (1.121), (1.122) можно найти компоненты тензора пла-

стической дисторсии uij0 и тензора пластической деформации εij,

отнесенные к произвольной ортогональной системе координат

и другие компоненты полярного тензора 2-го ранга uij0 − тензора пластической дисторсии. В итоге можно записать

Из-за ортогональности h и m следует, что

124

α(h1m1 + h2m2 + h3m3) = u110 + u220 + u330 = 0 .

Это означает сохранение объема при сдвиговой деформации. Тензор пластической дисторсии uij0 можно представить в виде

суммы симметричного тензора εij, описывающего чистую пластическую деформацию с пятью степенями свободы, и антисимметричного тензора ωij, характеризующего поворот кристаллической

решетки после пластической деформации: uij0 = εij + ωij.

Скольжение в металлах с ГЦК структурой. Плоскостями и направлениями скольжения, как правило, служат плоскости и направления плотнейшей упаковки. В металлах с ГЦК структурой системой скольжения является {111}<110>, т.е. имеется 8 плоскостей скольжения с шестью направлениями в каждой плоскости. Однако из-за центросимметричности скольжения имеется 12 различных систем скольжения, которые удобно представить на стереографической проекции.

Обычно ось растяжения F показывают в пределах стандартно-

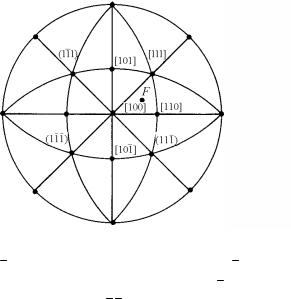
го стереографического треугольника [100]−[110]−[111] (рис. 1.77).

Рис. 1.77. Системы скольжения ГЦК кристалла на стандартной стереографической проекции:

(11 1)[101] − первичная система скольжения; (1 1 1)[110] − сопряженная или вторичная система скольжения; (111)[10 1] − критическая система скольжения; (1 1 1)[101] − поперечная система скольжения

125

Тогда первичной системой скольжения − с максимальным зна-

чением множителя Шмида − будет система (11 1)[101] . Благодаря

повороту в процессе растяжения ось F перемещается к направлению скольжения [101] и переходит в треугольник [100]−[101]− [111], в котором действует сопряженная (или вторичная) система

скольжения (1 1 1)[110] , и ось растяжения возвращается в стан-

дартный стереографический треугольник. Точно также при сжатии ось F смещается к направлению нормали к плоскости скольжения и

оказывается в треугольнике [100]−[110]−[111], где действует кри-

тическая система скольжения (111)[10 1] . Систему скольжения (1 1 1)[101] называют поперечной системой скольжения.

Скольжение в металлах с ОЦК структурой. Кристаллографи-

ческое скольжение включает плотнейшее направление <111>. В качестве плоскости скольжения могут быть плоскости {110}, {112} или {123} в зависимости от металла и температуры деформации.

Как правило, скольжение неполярно, т.е. оно может происходить как в прямом, так и в обратном направлении. Однако имеются случаи, когда скольжение в прямом и в обратном направлениях кристаллографически неэквивалентны. Полярность скольжения в этих случаях обусловлена несимметричным характером потенциального рельефа решетки. Критерием для полярного скольжения является несовпадение плоскости скольжения с плоскостью симметрии кристалла, когда направление скольжения является полярным вектором в плоскости скольжения. Типичным примером полярного скольжения служат системы скольжения {112}<111> и {123}<111> в ОЦК металлах.

В металлах с ОЦК структурой возможно некристаллографиче-

ское скольжение с направлением <111> и по плоскости с максимальным напряжением сдвига, когда χ = 90о − λ.

Скольжение в металлах с ГПУ структурой. В металлах с ГПУ структурой направлением скольжения является чаще всего направ-

ление 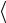2 1 10 , а в качестве плоскостей скольжения могут быть плоскости (0001) − базисное скольжение, {10 1 0} − призматическое

126

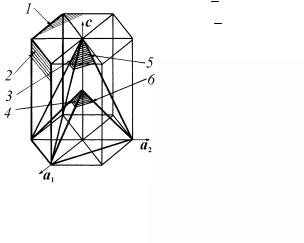
скольжение, {10 11}− пирамидальное I рода, {10 12}− пирамидальное II рода, {1121} − пирамидальное III рода {1122} − пирамидаль-

ное IV рода (рис. 1.78).

Рис. 1.78. Плоскости скольжения ГПУ кристаллах:

1 − базисного; 2 − призматического;

3 − пирамидального I рода;

4 − пирамидального II рода;

5 − пирамидального III рода;

6 − пирамидального IV рода

В металлах с отношением c/a > (c/a)теор = 1,633 при комнатной температуре действует базисная система скольжения (Zn, Cd), в

Mg для c/a ≈ (c/a)теор действует тоже базисная система скольжения. В α-Zr, α-Ti (c/a = 1,59 < 1,633) − призматическая система скольже-

ния, однако в Be c c/a = 1,57 < 1,633 опять действует базисная система скольжения.

Механическое двойникование кристаллов. Двойникование играет сравнительно небольшую роль в деформации и проявляется лишь тогда, когда деформация скольжением затруднена. Двойникованию способствует низкая температура и ударное нагружение, так как с понижением температуры и увеличением скорости деформации критическое напряжение для скольжения растет быстрее, чем для двойникования. Среди кристаллов металлов двойникование легче всего идет в гексагональных металлах, несколько труднее − в ОЦК металлах и труднее всего − в ГЦК металлах.

В отличие от трансляционного скольжения, когда смещение кратно периоду решетки, атомы при двойниковании смещаются на долю вектора трансляции решетки. Сдвиговая деформация при двойниковании является простым сдвигом, когда все атомы части кристалла, перешедшего в двойниковое положение, должны смещаться пропорционально их расстоянию от плоскости зеркального отражения. Эту плоскость называют плоскостью двойникования, а

направление смещения − направлением двойникования.

127

Двойниковый сдвиг, как и сдвиг при упругой деформации, явля-

ется однородной деформацией. Однородной сдвиговой деформаци-

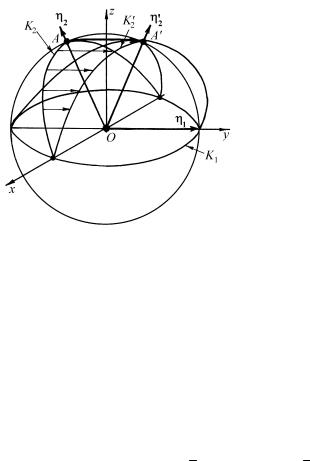
ей называется такая деформация, когда заданное макроскопическое изменение формы при двойниковании можно характеризовать эллипсоидом, в который превращается шар, мысленно выделенный в кристалле. Пусть верхняя часть такого шара единичного радиуса подвергается однородной деформации сдвигом вдоль плоскости K1

(рис. 1.79).

Рис. 1.79. Однородная сдвиговая деформация при двойниковании

Ось y расположена вдоль направления сдвига η1, а за ось z выберем нормаль к плоскости K1. У эллипсоида есть два круговых неискаженных сечения: первое − в плоскости сдвига K1, второе − в плоскости K2, проходящей перпендикулярно к плоскости чертежа через точку А'. В результате сдвига на s направление ОА (η2) без искажения переходит в ОА'.

Плоскости K1 и K2, а также направления η1 и η2 называются эле-

ментами двойникования, величину s − кристаллографическим сдвигом.

ВОЦК кристаллах K1 и K2 совпадают с {112}, η1 и η2 − с <111>,

ав ГЦК кристаллах K1 и K2 совпадают с {111}, а η1 и η2 с − <112>, причем в обоих случаях s = 0,707. В α-Zr в одной из систем двой-

никования K1 и K2 совпадают с {10 12}, а η1 и η2 − с 1011 .

128