
- •от ХХ УУУУ 20007 г. МГУП
- •Учебник подготовлен в рамках Инновационной образовательной программы
- •ISBN 978-5-7262-0821-3
- •ISBN 978-5-7262-0822-0 (т.1)
- •Глава 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
- •Предисловие к тому 1
- •Глава 1. ФИЗИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
- •1.1. Кристаллическое состояние
- •1.1.3. Решетка и структура кристаллов
- •1.2. Основы кристаллографии
- •1.2.1. Кристаллографические проекции
- •1.2.2. Пространственная решетка
- •1.2.3. Кристаллографические символы
- •1.2.4. Обратная решетка
- •1.2.5. Матрица ортогонального преобразования
- •1.2.6. Преобразование индексов направлений
- •1.3. Симметрия кристаллов
- •1.3.1. Поворотные оси симметрии
- •1.3.2. Инверсионные оси
- •1.3.3. Зеркально-поворотные оси
- •1.3.4. Элементы теории групп
- •1.3.5. Точечные группы симметрии
- •Бравэ
- •Бравэ
- •Распределение ячеек Бравэ по сингониям показано в табл. 1.4.
- •1.3.6. Пространственные группы
- •1.3.7. Предельные группы симметрии
- •1.4. Структура кристаллов
- •1.4.1. Плотнейшие упаковки в структурах
- •1.4.3. Структурные типы соединений типа АВ
- •1.4.4. Структурные типы соединений типа АВ2
- •1.4.5. Структурные типы соединений типа АmВnCk
- •1.4.7. Структура фуллеренов, фуллеритов
- •1.4.8. Структура поверхности
- •1.5. Физические свойства кристаллов
- •1.5.1. Принцип симметрии в кристаллофизике
- •1.5.4. Упругие свойства кристаллов
- •1.6. Кристаллография пластической деформации
- •1.6.1. Геометрия пластической деформации
- •1.6.2. Кристаллографическая текстура
- •1.7. Кристаллография границ зерен
- •1.7.1. Малоугловые границы
- •1.7.2. Высокоугловые границы
- •1.8. Кристаллография мартенситных превращений
- •1.8.1. Морфология мартенситных превращений
- •1.8.2. Кристаллография мартенситных превращений
- •Контрольные вопросы, задачи и упражнения
- •Глава 2. ДЕФЕКТЫ КРИСТАЛЛИЧЕСКОЙ СТРУКТУРЫ
- •2.1. Точечные дефекты
- •2.1.1. Вакансии и межузельные атомы
- •2.1.2. Энергия образования точечных дефектов
- •Контрольные вопросы
- •Список использованной литературы
- •Глава 3. ФИЗИКА ТВЕРДОГО ТЕЛА
- •3.1. Строение атомов и межатомные взаимодействия
- •3.1.1. Классификация конденсированных систем
- •3.1.4. Энергия связи кристаллов
- •3.1.5. Типы связи в твердых телах
- •Металлическая связь. В отличие от ковалентной связи, которая образуется между двумя соседними атомами в результате коллективизации двух валентных электронов, металлическая связь появляется вследствие коллективизации всех валентных электронов. Эти электроны не локализуются у отдельных атомов, а принадлежат всему коллективу атомов. Поэтому они называются свободными электронами, перемещающимися по всему объему металла и в каждый момент времени равномерно распределенными в нем. Классическим подтверждением наличия таких свободных электронов в металлах является опыт Мандельштама и Папалекси, когда при резкой остановке вращающейся катушки, сделанной из металлической проволоки, в ней возникал электрический ток. Ярким подтверждением этому являются высокие электро- и теплопроводность металлов.
- •Ионная связь. Атомы, стоящие в периодической системе Д. И. Менделеева рядом с инертными газами, обладают склонностью принимать их конфигурацию либо путем отдачи, либо путем принятия электронов. У атомов щелочных металлов, стоящих непосредственно за инертными газами, валентный электрон слабо связан с ядром, так как движется вне заполненного слоя. Поэтому этот электрон может быть легко удален от атома. У галоидов, стоящих непосредственно перед инертными газами, недостает одного электрона для заполнения устойчивого слоя благородного газа. Поэтому галоиды обладают высоким сродством к дополнительному электрону.
- •Изоморфизм и морфотропия. Рассмотрим несколько ионных соединений щелочных металлов с галоидом бромом: LiBr, NaBr, KBr, RbBr и CsBr. Первые четыре соединения имеют решетку типа NaCl, а пятое соединение CsBr кристаллизуется в решетке типа CsCl.
- •3.2. Основы электронной теории кристаллов
- •3.2.1. Квантовая теория свободных электронов
- •3.2.2. Зонная теория металлов
- •3.3. Теория фаз в сплавах
- •3.3.1. Классификация фаз в сплавах
- •3.3.2. Твердые растворы
- •3.3.3. Промежуточные фазы
- •1B3.4. Диффузия и кинетика фазовых превращений
- •2Bв металлах и сплавах
- •4B3.4.1. Линейные феноменологические законы
- •5B3.4.2. Макроскопическое описание явления диффузии
- •6B3.4.3. Атомная теория диффузии в металлах
- •9B3.4.5. Диффузия и фазовые превращения в металлах
- •10Bи сплавах
- •3B3.5. Электрические свойства твердых тел
- •11B3.5.1. Основы электронной теории электропроводности
- •14B3.5.3. Эффект Холла
- •15B3.5.4. Связь электросопротивления со строением сплавов
- •20B3.5.7. Сверхпроводимость
- •3.6. Магнитные свойства твердых тел
- •3.6.1. Основные определения. Классификация веществ по магнитным свойствам
- •3.6.2. Магнитные свойства свободных атомов
- •3.6.3. Физическая природа диамагнетизма
- •3.6.4. Физическая природа парамагнетизма
- •3.6.5. Магнитная восприимчивость слабых магнетиков
- •3.6.6. Основы теории магнитного упорядочения
- •3.6.7. Доменная структура ферромагнетиков
- •3.6.8. Магнитные свойства ферромагнетиков
- •3.6.9. Антиферромагнетики и ферримагнетики
- •3.7. Тепловые свойства твердых тел
- •3.7.2. Теплоемкость кристаллических твердых тел
- •3.7.3. Теплопроводность твердых тел
- •3.7.4. Термическое расширение твердых тел
- •3.8. Упругие свойства твердых тел
- •3.8.1. Основные характеристики упругости
- •3.8.2. Упругость чистых металлов и сплавов
- •3.8.3. Ферромагнитная аномалия упругости
- •3.8.5. Внутреннее трение
- •Контрольные вопросы
- •Список использованной литературы
E = 4ρν2рез L2.
Высокая точность определения резонансной частоты обуславливает и высокую точность определения модуля упругости.
3.8.2. Упругость чистых металлов и сплавов
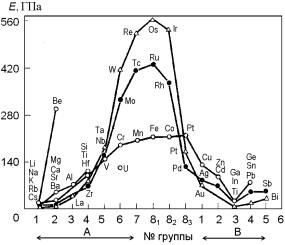
Из рис. 3.139 следует, что модуль упругости при комнатной температуре является периодической функцией атомного номера элемента.
У элементов третьего периода Na, Mg, A1 и Si модуль увеличивается вместе с атомным номером, что связано с увеличением числа валентных электронов и уменьшением атомного радиуса. Среди элементов одной группы, например, Be, Mg, Ca, Sr и Ва, с увеличением атомного номера модуль упругости уменьшается наряду с увеличением атомного радиуса. Можно принять, что модуль увеличивается с уменьшением междуатомного расстояния а приблизи-
тельно по уравнению:
Е = k/am,
где k и m – постоянные величины.
Рис. 3.139. Периодическое изменение модуля нормальной упругости элементов
611
Это правило не распространяется на переходные металлы. В отличие от простых металлов у переходных металлов одной группы (например, Os, Ru, Fe или Ir, Rh, Co) модуль упругости растет вместе с атомным радиусом, что теоретически не объяснено.
Модуль упругости переходных металлов относительно высок, что можно приписать значительной силе междуатомной связи, обусловленной d-электронами. Наибольшее значение модуля имеют элементы с 5 – 7 d-электронами (Os, Ru, Fe, Mo, Co и др.).
Очевидно, что фазовые превращения в металлах сопровождаются заметным изменением модулей упругости. Так, превращение α- Fe→γ-Fe повышает Е в связи с увеличением компактности решетки.
При полной растворимости в твердом состоянии, т. е. при однотипных пространственных решетках двух металлов и близкой их валентности и атомного радиуса, модуль упругости бинарного твердого раствора меняется линейно (Cu – Ni, Cu – Pt, Cu – Аu) или почти линейно (Ag – Au) в функции атомной концентрации. При наличии в растворе переходных металлов получается значительное отступление от аддитивности, причем кривая обращена выпуклостью вверх от оси концентраций.
В случае образования ограниченных твердых растворов было установлено, что изменение модуля упругости dE/dc тем больше, чем выше валентность Z растворенного вещества и линейно связано с произведением атомной концентрации и квадрата валентности этого вещества (cZ2).
Наряду с электронной концентрацией на модуль упругости влияет также разница атомных радиусов растворителя и растворенного вещества r. Теоретически установлено, что dE/dc пропорционально r2.
Из соображений, приведенных выше, следует, что факторы, понижающие температуру плавления сплава, должны понижать и его модуль упругости. Эксперименты в общем подтверждают, что понижение абсолютной температуры солидуса прямо пропорционально понижению модуля упругости, если сравнивать различные твердые растворы на базе одного компонента.
612
При упорядочении твердых растворов происходит увеличение сил межатомной связи и возрастание модулей упругости.
Упругие свойства химических соединений и промежуточных фаз в общем случае подчиняются правилу: чем выше температура плавления соединения (промежуточной фазы), тем выше значение модуля упругости.
Небольшая холодная деформация понижает величину модуля упругости твердых растворов (так же, как и чистых металлов). При больших степенях деформации возможно его увеличение из-за образования текстуры.
Ввиду сравнительно небольшой структурной чувствительности упругих свойств модуль упругости почти не зависит от величины зерна однофазного сплава и дисперсности гетерогенного сплава.
В двухфазных сплавах имеет место аддитивная зависимость модуля упругости от объемной концентрации фаз, составляющих сплав.
3.8.3. Ферромагнитная аномалия упругости
Наличие в ферромагнетиках явления магнитострикции (изменения линейных размеров при возникновении магнитного порядка) приводит к тому, что они имеют пониженный модуль упругости
Еферр = Енорм – E'.
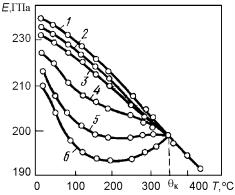
Рис. 3.140. Температурная зависимость модуля Юнга никеля ненамагниченного (6) и намагниченного в полях
0,48 (5); 0,8 (4); 3,28 (3); 8,48
кА/м (2) и до насыщения в поле 46 кА/м (1)
613
Приближение к точке Кюри при нагреве и переход в парамагнитное состояние устраняют ферромагнитную отрицательную составляющую Е', а выше точки Кюри имеет место нормальное изменение Е с температурой. При этом в некотором температурном интервале модуль упругости Еферр может даже возрастать при нагревании вследствие того, что Е' уменьшается больше, чем Енорм (рис. 3.140).
Измерение Е при наложении поля H = 46 кА/м (кривая 1), в котором никель намагничивается до насыщения, показывает, что модуль упругости изменяется нормально при любой температуре.
3.8.4.Общие сведения о релаксационных явлениях
иих механизмах
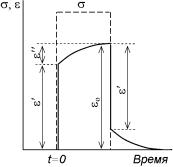
Все сказанное выше об упругости твердых тел относится к случаю, когда деформация точно следует за приложенным напряжением в соответствии с законом Гука σ = Еε. В действительности стабильная деформация в соответствии с законом Гука получается только при очень медленном нагружении образца. Рассмотрим изменение деформации со временем при очень быстром приложении к образцу растягивающего напряжения σ. В этом случае образец
практически мгновенно деформируется на величину ε′ и модуль нормальной упругости Ен будет равен σ/ε′
(рис. 3.141).
Если затем выдержать под этим напряжением образец до момента установления равновесия, то по ряду причин, рассматриваемых ниже, получится дополнительная деформация образца ε′′ и модуль Ер приобретет значение σ/(ε′+ε′′). Очевидно, что Ен > Ер. Первый из модулей называется нерелак-
сированным, второй – релаксирован-
614
ным. При мгновенном падении σ до нуля деформация снижается до ε′′, а затем постепенно уменьшается до нуля.
Время, необходимое для уменьшения деформации (при постоянном напряжении) в е раз, называется временем релаксации деформации при постоянном напряжении. Аналогично понятию «ре-
лаксация деформации» имеется и понятие «релаксация напряже-
ния». |
|
Понятие «релаксированный» и «нерелакси- |
|
рованный» модуль становится нагляднее, если |
|
рассмотреть диаграмму растяжения в упругой |
|
области (рис. 3.142). При быстром растяжении |
|
испытуемого образца от О до А в результате |
|
адиабатического процесса температура образ- |
|
ца будет ниже температуры окружающей сре- |
|
ды, и спустя некоторое время образец, погло- |
|
тив тепло из окружающей среды, удлинится до |
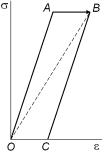
Рис. 3.142. Диаграмма |
точки В. При уменьшении нагрузки до точки С |
упругого |
температура образца окажется более высокой, |
последействия |
чем у окружающей среды. Цикл закончится |
|
охлаждением и сжатием до точки О, т. е. до первоначального значения. Тангенс угла наклона линии ОА дает адиабатический или нерелаксированный модуль Ен, а тангенс угла наклона линии OB – изотермический или релаксированный модуль Ер. Как видно, Ен > Ер.
Отставание деформации от приложенного напряжения наблюдается даже при малых напряжениях и приводит к существованию
втвердых телах релаксационных явлений. К их числу, помимо существования адиабатического и изотермического модулей упругости, относятся: зависимость упругих модулей от частоты деформирования, внутреннее трение, обратимая ползучесть и т. д.
Релаксация – это следствие запаздывания различных процессов
вкристаллической решетке образца. Эти запаздывания и определяют времена релаксации соответствующих процессов. Рассмотрим основные механизмы релаксационных процессов.
1.Релаксация, обусловленная тепловыми потоками. Рассмотрим изгиб пластины, как это показано на рис. 3.143.
615
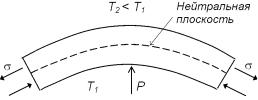
Рис. 3.143. Изгиб пластины (стрелками указано направление действия сил)
При изгибе есть нейтральная плоскость. Пусть часть пластины выше этой плоскости растянута, а ниже – сжата. В условиях мгновенного, адиабатического нагружения верхняя часть пластины охладится, а нижняя нагреется. При последующей выдержке под нагрузкой выравнивание температуры обеих частей приведет к тому, что растянутая часть будет нагреваться до установления теплового равновесия и, следовательно, дополнительно расширяться. Сжатая часть будет охлаждаться и испытает дополнительное сжатие. Другими словами, с течением времени пройдет релаксационный процесс, который увеличит стрелу прогиба до некоторого предельного значения при постоянной величине приложенного напряжения.
Выравнивание температуры может происходить в данном случае как между твердым телом и окружающей средой, так и между отдельными объемами тела.
2. Процессы релаксации, связанные с анизотропным рас-
пределением атомов в поле напряжений. В неупорядоченном твер-
дом растворе распределение атомов растворенного вещества не связано с каким-либо определенным кристаллографическим направлением. При наложении внешнего напряжения растворенные атомы стремятся перейти в положения, при которых решетка кристалла имеет минимум свободной энергии. Поясним это примером. Если растворенный атом в твердом растворе замещения имеет больший размер, чем атом растворителя, то такой атом, оказавшись в сжатых слоях, будет перемещаться в поле напряжений в места, где межатомное расстояние увеличено. Это приведет к тому, что атомы с большими радиусами окажутся теперь в сжатых слоях, что создаст в этих местах внутренние напряжения, которые будут релаксировать с определенным временем τ.
616
