1.7. Кристаллография границ зерен

Во всяком поликристаллическом материале существуют внутренние границы, разделяющие соседние зерна. Эти внутренние границы являются или границами зерен одной и той же фазы, или межфазными границами. В любом случае граница является двумерным дефектом, имеющим макроскопические размеры в двух измерениях и атомные − в третьем измерении, т.е. является наноструктурным компонентом.

Рассмотрим простейший случай − плоскую границу между двумя кристаллами. Для задания границы в таком бикристалле с мак-

роскопической точки зрения необходимы 5 параметров: 3 − для описания взаимного разворота двух кристаллов и 2 − для задания n − нормали к плоскости границы. В качестве угловых параметров разворота используют три эйлеровских угла (φ, θ, ψ) или угол разворота α и ось разворота u c кристаллографическими индексами <mnp>. Из трех компонентов оси разворота m, n, p независимыми являются только два, поскольку m:n:p = l1:l2:l3, но l12 +l22 +l32 =1 ,

где l1, l2, l3 − направляющие косинусы. При микроскопическом рассмотрении необходимо ввести вектор t = t1a1 + t2a2 + t3a3 , соеди-

няющий начала координат соседних кристаллов, где t1, t2, t3 выражается в долях трансляций. Таким образом, в общем случае требу-

132

1.7.1. Малоугловые границы

Малоугловые границы являются структурными границами, состоящими из дислокаций. Симметричная граница наклона состоит из стенки краевых дислокаций (рис. 1.84).

Если расстояние между дислокациями в стенке D, вектор Бюргерса b, угол разориентировки θ, то sin(θ/2) = b/(2D) и при малых углах sinθ ≈ θ

Малоугловая граница кручения состоит из сетки двух параллельных рядов винтовых дислокаций. При малых углах разориентировки выполняется соотношение (1.149), где D − расстояние между дислокациями одной серии.

В общем случае для малоугловых границ выполняется формула

где θ − угол разориентации, r − вектор в плоскости границы, который пересекают дислокации с суммарным вектором Бюргерса

d = ∑bi .

i

Угол разориентировки зерен или субзерен определяет энергию малоугловой границы:

133

где E0 и A − константы (E0 пропорциональна модулю сдвига и вектору Бюргерса). Таким образом, энергия малоугловой границы непрерывно растет с увеличением угла θ.

1.7.2. Высокоугловые границы

При рассмотрении структуры высокоугловых границ первоначально была предложена модель аморфной прослойки по границам зерен, обеспечивающей сцепление соседних зерен. Модель аморфной прослойки противоречит многим позднее установленным фактам. Во-первых, свойства аморфной границы не должны зависеть от взаимной ориентации соседних зерен. В действительности же энергия границ зерен, скорость диффузии по границам, скорость миграции границ, зернограничное скольжение зависят от взаимной разориентировки зерен. Следовательно, границы зерен не аморфны, не бесструктурны и должны иметь определенное строение, зависящее от кристаллографической разориентировки. Во-вторых, аморфная прослойка должна иметь достаточно большую толщину (порядка сотни атомных диаметров), чтобы обеспечить скольжение зерен неправильной формы. В то же время прямые экспериментальные данные, полученные с помощью ионного проектора, показывают, что границы имеют толщину всего в несколько межатомных расстояний.

Позднее была предложена модель переходной решетки толщиной в несколько атомных диаметров, в которой атомы занимают промежуточные положения между положениями узлов соседних решеток. Естественно, что строение границы переходной зоны зависит от разориентировки соседних зерен. Следующим важным шагом в изучении границ зерен была островковая модель Мотта, согласно которой граница состоит из областей «хорошего» и «плохого» сопряжения решеток двух зерен.

В настоящее время эту модель в ее первоначальном виде уже не используют, но общую идею о чередовании в структуре границы областей хорошего и плохого сопряжения широко применяют в большинстве современных моделей высокоугловых границ.

134

Решетка совпадающих узлов (РСУ) (в английской терминоло-

гии − coinsidence site lattice, CSL) возникает при определенных строго фиксированных значениях оси и угла разворота соседних кристаллов (соотношения Кронберга–Вильсона). Например, при повороте на угол θ = 2arctg(1/2) = 36,9° вокруг оси [100] возникает решетка, в которой совпадающие узлы лежат в каждой пятой плос-

узлов является тетрагональной.

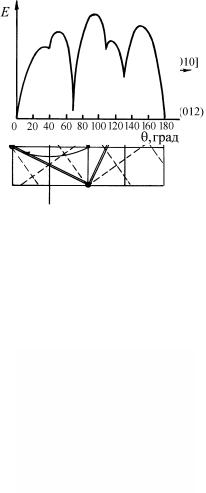
Специальные (особые или регулярные) границы возникают, ко-

гда граница совпадает с наиболее плотно упакованной плоскостью решетки совпадающих узлов; при этом энергия границы минимальна, а на графике зависимости энергии границы зерна от угла разворота наблюдаются резкие спады (рис. 1.86).

135

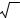
Специальные свойства границ зерен сохраняются при небольших отклонениях взаимной ориентации решеток соседних зерен от специальной, при этом в структуре границы зерна появляются зернограничные дислокации, выполняющие аккомодационную роль, приспосабливая структуру границы к конкретной разориентировке зерен.

Максимальный угол отклонения (в радианах) от специальной ориентировки, когда еще возможна аккомодация с помощью зернограничных дислокаций и сохраняются специальные свойства, определяется как

Для описания разворота кристаллов обычно используют такие параметры как угол θ и ось разворота l, а множество всевозможных разворотов можно представить в виде шара радиуса π. Объем пространства разворотов, как и ориентационного пространства с эйлеровскими углами, равен 8π2. Для описания разворота удобно использовать матрицу поворота A0 (l,θ), см. (1.60). Если кристалли-

ческое пространство обладает элементами симметрии Ri, то, в соответствии с правилом Вигнера в теории групп, возникают эквивалентные описания того же самого разворота Аi, причем

Таким образом, для описания разворота двух зерен в кубическом материале с группой симметрии m3m существует 24 способа с 24 значениями углов разворота θi. Максимально возможное значение минимального угла разворота вокруг оси l с кристаллографическими индексами [mnp] называют предельным углом разворота θпр вокруг [mnp]. Если угол разворота θ > θпр, то возможно эквивалентное описание с углом разворота θi < θ. Предельный угол разворота для [100] равен 45°, для [110] − 61°, для [111] − 60°. Максимальное значение предельного угла разворота для кубических кристаллов равно ≈ 62° вокруг [221].

Полная решетка наложения (ПРН). Если РСУ является пере-

сечением множества узлов двух решеток LРСУ = L1 IL2 , то полная решетка наложения (в английской терминологии − displacement

136