Если при повороте система координат xyz переходит в x'y'z' (рис. 1.25,б), то ось поворота l можно определить по пересечению меридианов B1 и B2. Каждый из них проходит через гномостереографическую проекцию плоскости Nyy' или Nzz' и соответствующую биссектрису b1 или b2. Угол поворота α измеряют в плоскости Pl между

точками ZP и ZP' , являющимися проекциями z и z' на плоскость Pl.

а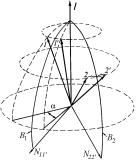

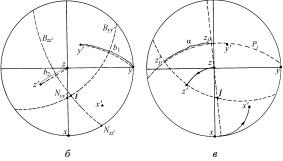
Рис. 1.25. Определение оси и угла поворота в пространстве (а) и на стереографической проекции (б, в)

1.2.2. Пространственная решетка

Любой узел пространственной решетки определяется линейной формой:

где a1, a2, a3 – векторы трансляций, а m1, m2, m3 – целые числа. Начало координат при этом может быть выбрано в любом узле пространственной решетки

Пространственная решетка может быть получена бесконечным параллельным повторением параллелепипеда, построенного на векторах кратчайших трансляций (базисных векторах) a1, a2, a3. Такой параллелепипед называют элементарной ячейкой. Можно показать, что при сделанном выборе трансляций элементарная ячейка не содержит узлов, находящихся на ее гранях или внутри объема. Такую ячейку называют примитивной или простой. Всякий узел примитивной ячейки принадлежит одновременно восьми

37

смежным ячейкам, поэтому примитивная ячейка содержит только один узел решетки.

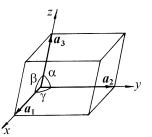
Длины векторов a1, a2, a3 и углы между ними α1, α2, α3 называют параметрами решетки, иногда их обозначают как a, b, c и α, β и γ соответственно (рис. 1.26).

Для описания кристаллического веще-

ства используют кристаллографическую систему координат с векторами транс-

ляций a1, a2, a3 (a, b, c) В общем случае Рис. 1.26. Элементарная это шесть параметров: косоугольные ко-

ячейка

ординаты с неодинаковыми масштабны-

ми отрезками по осям:

a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90о.

Пространственные решетки по симметрии расположения узлов разделяются на семь видов, называемых сингониями (табл. 1.1).

Таблица 1.1

Кристаллографические системы координат

Важной характеристикой кристаллографической системы является метрическая матрица G = {gij}, элементы которой определяются скалярными произведениями базисных векторов:

gij = (ai aj). (1.11)

Так как скалярные произведения коммутативны, то метрическая матрица всегда симметрична: gij = gji.

38

Из определения метрической матрицы следует, что длина базисных векторов равна

углы αij между базисными векторами определяются соотношением

а определитель метрической матрицы равен квадрату объема эле-

В некоторых случаях для описания пространственной решетки используют сложные элементарные ячейки, ребра которых не являются кратчайшими трансляциями, а в центрах граней или в центре объема имеются дополнительные узлы (правила выбора элементарных ячеек будут рассмотрены в дальнейшем). В этом случае положение узла в решетке задается вектором Rmn = Rm + Rn, где вектор Rn определяет положение дополнительных узлов

Rn = n1a1 + n2a2 + n3a3, (1.15) n1, n2, n3 – дробные числа, являющиеся координатами транляцион-

но неидентичных узлов внутри элементарной ячейки, т.е. базис решетки. В матричном виде базисы объемноцентрированной (I), гранецентрированной (F), и A-центрированной решеток (A) имеют вид:

39

1.2.3. Кристаллографические символы

Символы узла. Положение любого узла в пространственной решетке определяется вектором Rmnp

Rmnp = ma + nb + p c. (1.16)

Три целых числа m, n, p однозначно определяют положение узла и называются индексами данного узла. Совокупность чисел m, n, p, записанная в двойных квадратных скобках [[m1 m2 m3]], называется символом узла. Узлы, лежащие на одной прямой, имеют пропорциональные индексы. Числа в символе пишутся подряд, без запятых, читаются порознь. Запятые ставятся лишь в тех (редчайших) случаях, когда индекс двузначен. Знак минус пишется над цифрой.

Например, [[1 2 0]] читается «один, минус два, ноль».

В сложных решетках для всех узлов, не лежащих в вершинах элементарных ячеек, числа m1, m2, m3 будут дробными. Например, узел, находящийся в центре объема ячейки и ближайший к началу координат, имеет символы [[½ ½ ½ ]], а узел в центре одной из гра-

ней – [[0 ½ ½ ]].

Символы узловой прямой. Решетку можно представить как семейство параллельных узловых прямых. Это семейство можно характеризовать прямой, проходящей через начало координат, которое принимается за первую точку, определяющую данную прямую. Второй определяющей точкой является ближайший узел с целочисленными координатами. Координаты этого узла, взятые в квадратные скобки, принимают за кристаллографический символ прямой [mnp]. Индексы важнейших направлений в кубическом кристалле приведены на рис. 1.27.

Оси координат имеют символы: ox – [100], oy – [010], oz – [001]. Одно из основных преимуществ кристаллографической символики

40

состоит в неизменности символов осей координат от сингонии кристалла.

Рис. 1.27. Индексы важнейших направлений в пространстве (а) и на стереографической проекции (б)

Индексы в угловых скобках <mnp> используют для обозначения направлений определенного типа, связанных элементами симметрии. Например, для кубической сингонии символ <100> обозначает

направления [100], [010] и [001], а также [100], [010], [001], т.е.

направления, индексы которых отличаются либо перестановкой, либо знаком.

В сложных ячейках можно выделить примитивные ячейки, построенные на кратчайших векторах трансляций. Так, в случае гранецентрированной кубической (ГЦК) решетки примитивная ячейка будет построена на векторах ½ a[110], ½ a[011], ½ a[101] (рис. 1.28).

41

Примитивная ячейка для объемно-центрированной кубической (ОЦК) решетки построена на векторах ½a[11 1 ], ½a[ 1 11], ½a[1 1 1] (рис. 1.29).

Базисные векторы примитивной решетки можно представить в матричном виде как

Символы плоскости. Пространственная решетка может быть представлена семейством параллельных узловых плоскостей. Пусть одна из таких плоскостей семейства отсекает на осях координат отрезки A, B, C. Уравнение такой плоскости в отрезках мож-

Переменные x, y, z в этом уравнении являются координатами узлов пространственной решетки, лежащих в данной плоскости, поэтому они равны целому числу m, n, p трансляций по каждой из осей:

Так как правая часть уравнения (1.20) равна единице, то отношения a/A, b/B, c/C представляют собой рациональные числа. В этом случае отношение между ними всегда будет равно отношению трех

Кристаллографическими индексами плоскости (индексами Мил-

лера) называют три целых простых числа h, k, l, которые являются обратным отношением длин отрезков, отсекаемых плоскостью на осях координат, выраженных в соответствующих длинах трансляций. Индексы, заключенные в круглые скобки, называют кристал-

лографическим символом плоскости (hkl). Учитывая пропорцио-

нальность индексов

42

h = q (a/A), k = q (b/B), l = q (c/C)

и подставляя их в исходное уравнение плоскости, получаем

где q – целое число. Для плоскости, проходящей через начало ко-

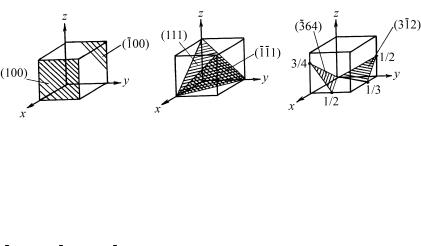
На рис. 1.30 показано расположение различных кристаллографических плоскостей в кубической элементарной ячейке.

Рис. 1.30. Расположение различных плоскостей в кубической элементарной ячейке

Символ в фигурных скобках {hkl} используют для обозначения плоскостей определенного типа, связанных элементами симметрии, и называется кристаллической формой. Например, для кубической сингонии символ {100} отвечает плоскостям (100), (010), (001),

(100), (010), (001), связанных между собой преобразованиями симметрии. Число плоскостей p в кристаллической форме называют множителем повторяемости. Так, в кубической сингонии для

{100} p = 6, для {110} p = 12, {111} p = 8, {123} p = 48. Следует отметить, что плоскости, принадлежащие одной кристаллической форме, характеризуются одинаковым межплоскостным расстоянием, т.е. одинаковым расстоянием между двумя соседними параллельными плоскостями.

Четвертый индекс в гексагональной системе. Элементарная ячейка в гексагональной решетке определяется двумя равными векторами a1 и a2, расположенными под углом 120о друг к другу, и осью c, находящейся под прямым углом к плоскости, в которой лежат векторы a1 и a2, называемой базисной плоскостью. Узлы ре-

43

шетки, расположенные в базисной плоскости, имеют гексагональную симметрию и характеризуются тремя равноправными осями

a1, a2 и a3 (рис. 1.31).

Поэтому в гексагональной системе принято определять положение плоскости с помощью четырех индексов (hkil), где четвертый индекс i берется по оси a3. Так как для определения положения плоскости в пространстве достаточно трех индексов, то четвертый индекс не является независимым, а выражается через остальные.

Проведем в гексагональной системе координат плоскость, следом которой в базисной плоскости будет отрезок AB; эта плоскость отсекает на оси

a1 отрезок OA = A1, на оси a2 – отрезок OB = A2 и на оси a3 – отрицательный отрезок OD = – A3 (см. рис. 1.31). Проведем из точки D прямую, параллельную оси a2. Из подобия получившихся тре-

Так как индексы являются величинами, обратными отрезкам, отсекаемым плоскостью на осях координат, и по оси a3 отсекается отрицательный отрезок, то

44

рех индексов легко обнаруживаются равнозначные плоскости. Однако расчеты в гексагональной системе для упрощения проводят с помощью трех индексов. Четвертый индекс часто опускается и заменяется точкой, т.е. записывается (hk.l).

Символом {hkil} обозначают симметрично-равнозначные (эквивалентные) плоскости, которые переводятся друг в друга какимлибо элементом симметрии.

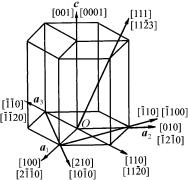
Система обозначений с четырьмя индексами может быть использована и для направлений в гексагональной решетке. Если в системе с тремя индексами направление R записывается в виде

Так как в гексагональной системе a3 = – (a1 + a2), то, учитывая условие (1.29), выражение (1.28) можно переписать в виде

Решение системы уравнений (1.31) относительно u, υ, w имеет вид u = (2U – V)/3, υ = (2V – U)/3, откуда, приводя индексы направлений к общему знаменателю, получим:

u = 2U – V, υ = 2V – U,

обозначений с тремя индексами к обозначениям, в которых используются четыре индекса, даны на рис. 1.33.

Обозначения в четырех индексах позволяют найти симметричноравнозначные (эквивалентные) направления <u υ t w>.

45