1.2.4. Обратная решетка

Важную роль в структурной кристаллографии играет обратная решетка, базисные векторы bj которой задаются соотношением

(ai bj) = δij, (1.33)

где δij – символ Кронекера; δii = 1; δij = 0 (i, j = 1, 2, 3).

Из соотношения (1.33) следует, что вектор b1 перпендикулярен к векторам a2 и a3, поэтому его направление определяется векторным произведением

Умножая выражение (1.34) скалярно на a1 и учитывая соотношение (1.33), получаем γ = 1/V, где V = a1 [a2×a3] отвечает объему ячейки, построенной на базисных векторах прямой решетки. Таким

Базисные векторы b2 и b3 получают циклической перестановкой соотношения (1.35).

Как видно из (1.33), прямая и обратная решетки являются взаимно обратными, и, если известны векторы обратной решетки b1, b2

Векторы a1, a2, a3 образуют базис прямой решетки, а b1, b2, b3 – базис обратной решетки. Базисные векторы обратной решетки иногда обозначают как a*, b*, c*.

В физике твердого тела обратная решетка задается соотношением, отличным от (1.33):

46

Длины базисных векторов обратной решетки равны bi = (gii)1/2, а углы между базисными векторами βij определяются из соотношения

Найдем соотношение, связывающее метрические матрицы прямого G и обратного G–1 базисов. Матричное выражение для произвольного вектора x в прямом и обратном базисе имеет вид

получим:

47

Обратные метрические матрицы для некоторых сингоний имеют вид:

Базисные векторы прямой и обратной решеток можно представить в виде матриц A и B, причем, если базисные векторы a1, a2, a3 прямой решетки в A представлены строками, а базисные векторы b1, b2, b3 обратной решетки – столбцами в B, то (1.33) можно записать как AB = I, или

Если матрица A состоит из базисных векторов ГЦК решетки в прямом пространстве, то A–1 – соответствует базисным векторам ОЦК решетки в обратном пространстве:

Причем, если ГЦК решетка в прямом пространстве построена на векторах длиной a и объемом a3, то в обратном пространстве ей соответствует ОЦК решетка, построенная на векторах длиной 2/a и объемом 8/a3.

48

Вектор обратной решетки. Произвольный узел обратной ре-

шетки определяется вектором обратной решетки HHKL

HHKL = Hb1 + Kb2 + Lb3,

где H, K, L – целые числа с общим множителем q, т.е. H = qh, K = qk, L = ql.

Свойства вектора обратной решетки. Пусть вектор

Rmnp = ma + nb + pc

находится в плоскости (hkl), проходящей через узел [[000]] (для такой плоскости q = 0), и уравнение плоскости имеет вид

Поскольку это соотношение выполняется для любого вектора Rmnp, лежащего в плоскости (hkl), то вектор Hhkl перпендикулярен плоскости

(hkl) (рис. 1.34).

Соотношение (1.52) можно рас-

сматривать как условие зональности (соотношение Вейсса), т.е. принад-

лежности плоскости (hkl) зоне плоскостей с осью [mnp], заданной на-

правлением Rmnp.

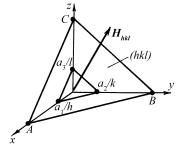
Плоскость (hkl), ближайшая к нулевому узлу, отсекает на оси OX отрезок a1/h, поэтому проекция a1/h на единичный вектор

Таким образом, вектор обратной решетки Hhkl по направлению совпадает с нормалью к плоскости (hkl), а по модулю равен обратному значению межплоскостного расстояния dhkl.

В дифракционных методах исследования, в частности в методе Лауэ, гномостереографические проекции плоскостей называют точками первого рода, а стереографические проекции направлений − точками второго рода. В кубических кристаллах все точки пер-

49

вого и второго рода совпадают, в тетрагональных кристаллах точки первого рода {hk0} и {001} совпадают с точками второго рода <hk0> и <001> соответственно. В гексагональных кристаллах точки первого рода в четырех индексном обозначении {hki0} и {0001} совпадают с точками второго рода <hki0> и <0001>, а в трех индексном обозначении {hk0} и <hk0> не совпадают, тогда как {001}

и<001> совпадают.

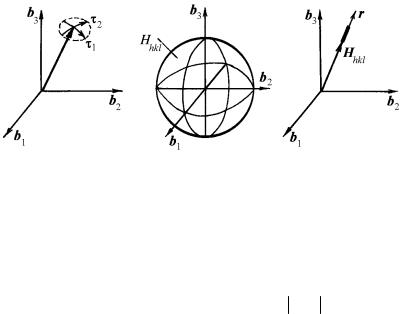
Вфизической кристаллографии рассматривают вектор обратной решетки не только для идеального монокристалла, но и для мозаичного монокристалла. В этом случае узел обратной решетки будет выглядеть не в виде точки, где заканчивается вектор обратной решетки, а в виде некоторой области, размытой по поверхности сфе-

ры радиуса Hhkl = Hhkl (рис. 1.35,а), т.е. вектор обратной решетки размывается в тангенциальных направлениях τ1 и τ2.

Рис. 1.35. Узлы обратной решетки мозаичного монокристалла (а), поликристалла (б), монокристалла в поле неоднородных упругих деформаций (в)

При рассмотрении идеального поликристалла, состоящего из случайно разориентированных монокристаллов, узел обратной ре-

шетки будет изображаться сферой радиуса R = Hhkl (рис. 1.35,б).

Если монокристалл находится в поле неоднородных упругих деформаций, то межплоскостное расстояние dhkl изменяется, и узел обратной решетки размывается в радиальном направлении r (рис. 1.35,в). Множество узлов прямой или обратной решеток можно задать решеточной функцией (функцией Дирака), в каждом узле которой находится δ-функция:

50