Экспериментальное определение скоростей молекул
Опыты по определению скорости молекул доказали справедливость формулы (4.7.3). Один из опытов был осуществлен немецким физиком О. Штерном в 1920 г.
Схема опыта показана на рисунке 4.15. Прибор состоит из сосуда 1, системы диафрагм 2, 3 и цилиндра 4, вращающегося с большой угловой скоростью со.
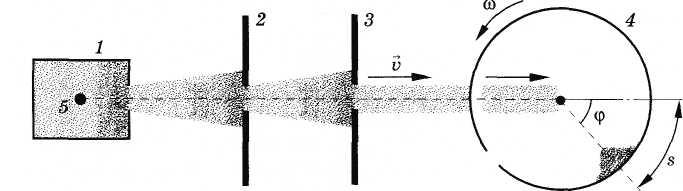
Рис. 4.15
В сосуде 1 натянута тонкая платиновая проволочка 5, покрытая слоем серебра. По проволочке пропускают электрический ток. При прохождении тока слой серебра испаряется и сосуд заполняется газом из атомов серебра. Газ находится в равновесном состоянии при температуре Т, которую можно измерить.
В стенке сосуда 1 имеется маленькое отверстие, через которое небольшое количество атомов серебра вылетает из сосуда в пространство, где создан высокий вакуум. Здесь атомы практически не сталкиваются друг с другом.
С
помощью диафрагм 2,
3 выделяется
пучок атомов, направленный вдоль диаметра
вращающегося цилиндра. В цилиндре
имеется узкая щель. В момент, когда щель
оказывается на пути пучка, небольшая
порция атомов попадает внутрь цилиндра
и движется к его противоположной стенке.
Расстояние, равное диаметру цилиндра
D,
эти
атомы пролетают за время
,
где
—
среднее значение скорости. За это время
цилиндр повернется на угол
.
Если
бы цилиндр был неподвижен, то атомы
осаждались бы на его внутренней
поверхности прямо против щели. Но при
вращении цилиндра атомы попадают на
участок цилиндра, смещенный на расстояние
от точки, лежащей на одном диаметре со
щелью (см. рис. 4.15).
На внутренней поверхности цилиндра образуется след от осажденного серебра в виде темного пятна. Толщина пятна не везде одинакова. На определенном участке толщина слоя серебра максимальна. Измерив длину дуги s, соответствующую наибольшей толщине слоя серебра, и зная диаметр цилиндра и его угловую скорость, можно определить среднюю скорость молекул по формуле:
(4.7.4)
Согласие со значением средней квадратичной скорости, вычисленной по формуле (4.7.3), оказывается вполне удовлетворительным. Это служит экспериментальным доказательством справедливости формулы (4.7.3), а значит, и выражения (4.5.5), из которого следует, что средняя кинетическая энергия прямо пропорциональна абсолютной температуре.
Измеряя толщину пятна серебра в разных местах, можно приблизительно подсчитать число атомов, скорости которых лежат в тех или иных интервалах. Таким образом осуществляется опытная проверка максвелловского распределения молекул по скоростям. Согласие с экспериментом для распределения Максвелла также оказывается удовлетворительным.
Средняя скорость броуновской частицы
Формула (4.7.2) позволяет понять, почему интенсивность броуновского движения возрастает с повышением температуры жидкости и уменьшается при увеличении массы частицы. Ведь броуновская частица участвует в тепловом движении молекул. Поэтому ее средняя кинетическая энергия также определяется формулой (4.5.5), а средняя квадратичная скорость — формулой
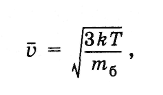
где тб — масса броуновской частицы. Если масса частицы велика, то средняя скорость ее движения настолько мала, что движение частицы практически обнаружить нельзя.
Скорость броуновской частицы в жидкости измерить непосредственно невозможно из-за крайней нерегулярности броуновского движения.
Средние скорости молекул превышают скорость звука и достигают сотен метров в 1 с. Эти скорости удалось измерить благодаря тому, что макроскопическому телу (цилиндру в опыте Штерна) можно сообщить столь большую угловую скорость, что за время пролета молекул внутри цилиндра он поворачивается на заметную величину.