Распределение модулей скоростей молекул

Найдем среднее число молекул, скорости которых по модулю лежат в интервале от v до v + Δv.

Распределение Максвелла (4.6.4) определяет число молекул, проекции скоростей которых лежат в интервалах значений от v_x до v_x + Δv_x, от v_y до v_y + Δv_y, от v_z до v_z + Δv_z. Векторы этих скоростей оканчиваются внутри объема Δv_xΔv_yΔv_z (см. рис. 4.8). Таким образом задается среднее число молекул, имеющих определенный модуль и определенное направление скоростей, задаваемые положением объема Δv_xΔv_yΔv_z в пространстве скоростей.

Все молекулы, модули скоростей которых лежат в интервале от v до v + Δv, располагаются в пространстве скоростей внутри шарового слоя радиусом v и толщиной Δv (рис. 4.10). Объем шарового слоя равен произведению площади поверхности слоя на его толщину: 4πv²Δv. Число молекул, находящихся внутри этого слоя и, следовательно, обладающих заданными значениями модуля скорости в интервале от v до v + Δv, может быть найдено из формулы (4.6.2), если заменить объем Δv_xΔv_yΔv_z на объем 4πv²Δv.

Рис. 4.10

Таким образом, искомое среднее число молекул равно:

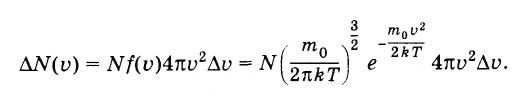(4.6.7)

Так как вероятность определенного значения модуля скорости молекулы равна отношению , то для плотности вероятности получим:

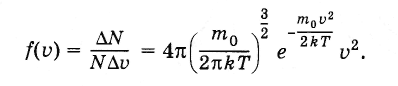(4.6.8)

График, выражающий зависимость этой функции от скорости, показан на рисунке 4.11. Мы видим, что функция f(v) имеет максимум уже не в нуле, как плотность вероятности f(v_x, v_y, v_z). Причина этого состоит в следующем. Плотность точек, изображающих молекулы в пространстве скоростей, по-прежнему будет наибольшей вблизи v = 0, но за счет роста объемов шаровых слоев с увеличением модулей скоростей (~ v²) происходит увеличение функции f(v). При этом число точек внутри шарового слоя растет быстрее, чем убывает функция f(v_x, v_y, v_z) вследствие уменьшения плотности точек.

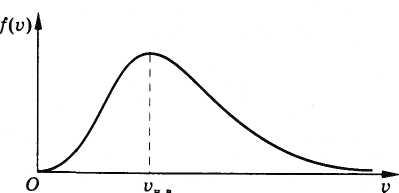
Рис. 4.11

Можно пояснить сказанное наглядным примером. Допустим, обычную мишень с концентрическими кругами обстреливает достаточно меткий стрелок. Попадания пуль концентрируются вокруг центра мишени. Плотность попаданий — число попаданий на единицу площади — будет максимальной вблизи центра мишени. Разделим мишень на отдельные узкие полоски шириной Ах (рис. 4.12, а). Тогда отношение числа попаданий на данную полоску к ее ширине будет максимально вблизи центра мишени. Зависимость отношения числа попаданий в данную полоску к ее ширине имеет вид, показанный на рисунке 4.12, б. Здесь опять получается гауссова кривая, как и для распределения f(vx) по проекциям скоростей (см. рис. 4.9).

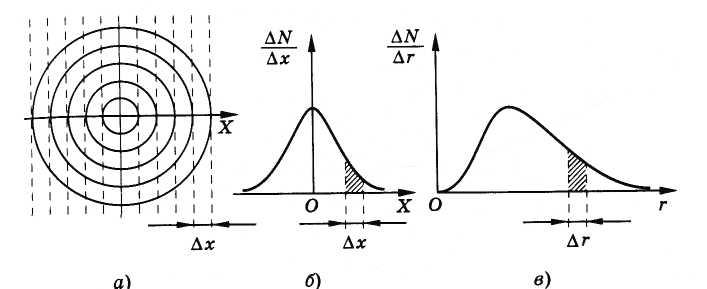
Рис. 4.12

Но совсем другой результат получится, если подсчитывать число попаданий в различные кольца мишени. В этом случае отношение числа попаданий в кольцо радиусом r к его ширине графически будет характеризоваться кривой, изображенной на рисунке 4.12, в. Хотя плотность попаданий по мере удаления от центра мишени убывает, но площади колец растут пропорционально г, что и приводит к смещению максимума кривой от нуля.

Наиболее вероятная скорость молекул

Зная формулу (4.6.8) для плотности вероятности модулей скоростей молекул, можно найти значение скорости, соответствующей максимуму плотности этой вероятности*. Скорость (ее называют наиболее вероятной) оказывается равной:

* Это делается по правилам нахождения максимума известной функции. Нужно вычислить производную этой функции по скорости и приравнять ее нулю.

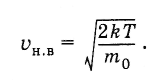(4.6.9)

Большинство молекул имеют скорости, близкие к наиболее вероятной (см. рис. 4.11).

По мере увеличения абсолютной температуры Т наиболее вероятная скорость увеличивается и при этом кривая зависимости f(u) становится все более сглаженной (рис. 4.13).

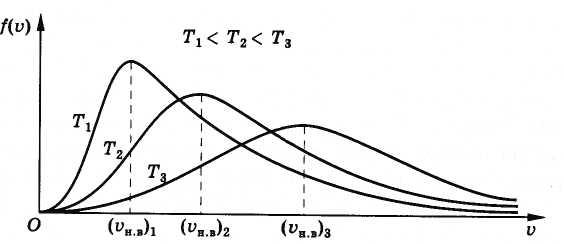
Рис. 4.13