Постоянная Больцмана
Больцман Людвиг (1844—1906) — великий австрийский физик, один из основоположников молекулярно-кинетической теории. В трудах Больцмана молекулярно-кинетическая теория впервые предстала как логически стройная, последовательная физическая теория. Больцман дал статистическое истолкование второго закона термодинамики. Им много сделано для развития и популяризации теории электромагнитного поля Максвелла. Борец по натуре, Больцман страстно отстаивал необходимость молекулярного истолкования тепловых явлений и принял на себя основную тяжесть борьбы с учеными, отрицавшими существование молекул.
В уравнение (4.5.3) входит отношение универсальной газовой постоянной R к постоянной Авогадро NA. Это отношение одинаково для всех веществ. Оно называется постоянной Больцмана, в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории.
Постоянная Больцмана равна:
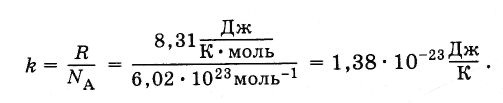(4.5.4)
Уравнение (4.5.3) с учетом постоянной Больцмана записывается так:
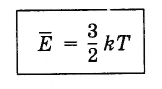(4.5.5)
Физический смысл постоянной Больцмана
Исторически
температура была впервые введена как
термодинамическая величина, и для нее
была установлена единица измерения —
градус (см. § 3.2). После установления
связи температуры со средней кинетической
энергией молекул стало очевидным, что
температуру можно определять как среднюю
кинетическую энергию молекул и выражать
ее в джоулях или эргах, т. е. вместо
величины Т
ввести
величину Т*
так,
чтобы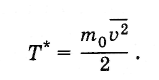
Определенная таким образом температура связана с температурой, выражаемой в градусах, следующим образом:
Поэтому постоянную Больцмана можно рассматривать как величину, связывающую температуру, выражаемую в энергетических единицах, с температурой, выраженной в градусах.
Зависимость давления газа от концентрации его молекул и температуры
Выразив Е из соотношения (4.5.5) и подставив в формулу (4.4.10), получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
(4.5.6)
Из формулы (4.5.6) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Средняя кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре. Коэффициент пропорциональности — постоянную Больцмана k = 10-23Дж/К — надо запомнить.
§ 4.6. Распределение максвелла
В большом числе случаев знание одних средних значений физических величин недостаточно. Например, знание среднего роста людей не позволяет планировать выпуск одежды различных размеров. Надо знать приблизительное число людей, рост которых лежит в определенном интервале. Точно так же важно знать числа молекул, имеющих скорости, отличные от среднего значения. Максвелл первым нашел, как эти числа можно определять.
Вероятность случайного события
В §4.1 мы уже упоминали, что для описания поведения большой совокупности молекул Дж. Максвелл ввел понятие вероятности.
Как неоднократно подчеркивалось, в принципе невозможно проследить за изменением скорости (или импульса) одной молекулы на протяжении большого интервала времени. Нельзя также точно определить скорости всех молекул газа в данный момент времени. Из макроскопических условий, в которых находится газ (определенный объем и температура), не вытекают с необходимостью определенные значения скоростей молекул. Скорость молекулы можно рассматривать как случайную величину, которая в данных макроскопических условиях может принимать различные значения, подобно тому как при бросании игральной кости может выпасть любое число очков от 1 до 6 (число граней кости равно шести). Предсказать, какое число очков выпадет при данном бросании кости, нельзя. Но вероятность того, что выпадет, скажем, пять очков, поддается определению.
Что же такое вероятность наступления случайного события? Пусть произведено очень большое число N испытаний (N — число бросаний кости). При этом в N' случаях имел место благоприятный исход испытаний (т. е. выпадение пятерки). Тогда вероятность данного события равна отношению числа случаев с благоприятным исходом к полному числу испытаний при условии, что это число сколько угодно велико:
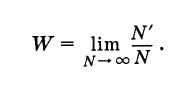(4.6.1)
Для
симметричной кости вероятность любого
выбранного числа очков от 1 до 6 равна
.
Мы
видим, что на фоне множества случайных
событий обнаруживается определенная
количественная закономерность, появляется
число. Это число — вероятность —
позволяет вычислять средние значения.
Так, если произвести 300 бросаний кости,
то среднее число выпаданий пятерки, как
это следует из формулы (4.6.1), будет равно:
300 ·
= 50, причем совершенно безразлично,
бросать 300 раз одну и ту же кость или
одновременно 300 одинаковых костей.
Несомненно, что поведение молекул газа в сосуде гораздо сложнее движения брошенной игральной кости. Но и здесь можно надеяться обнаружить определенные количественные закономерности, позволяющие вычислять статистические средние, если только ставить задачу так же, как в теории игр, а не как в классической механике. Нужно отказаться от неразрешимой задачи определения точного значения скорости молекулы в данный момент и попытаться найти вероятность того, что скорость имеет определенное значение.