§1.5.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом

Несмотря на внешнюю простоту телеграфных уравнений, их ана­литическое решение для произвольных сопротивлений генератора, нагрузки и сигнала произвольной формы отсутствует. Применение операторного метода, как было показано ранее, позволяет суще­ственно упростить отыскание мгновенных значений напряжения u(x,t) и тока i(x,t).

Ограничимся рассмотрением линейной, однородной, инвариант­ной во времени длинной линией. В этом случае уравнение будет иметь вид:

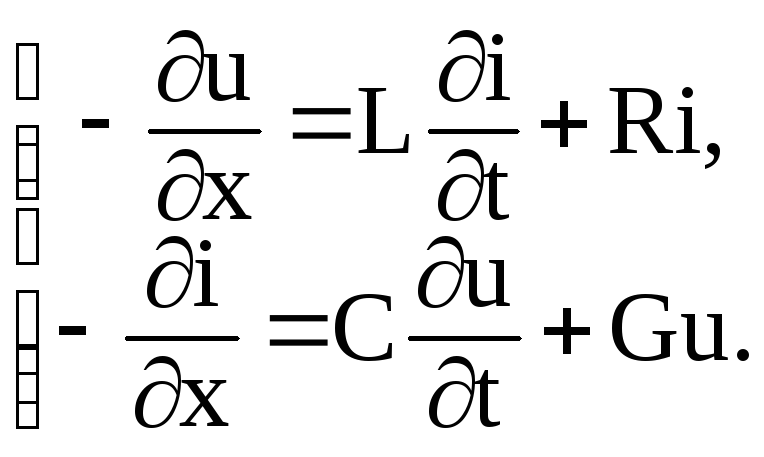(1.39)

Напряжение u(x,t) и токи i(x,t) в длинной линии, а также источники, как и ранее, удовлетворяют условию принадлежности к классу оригиналов.

В этом случае

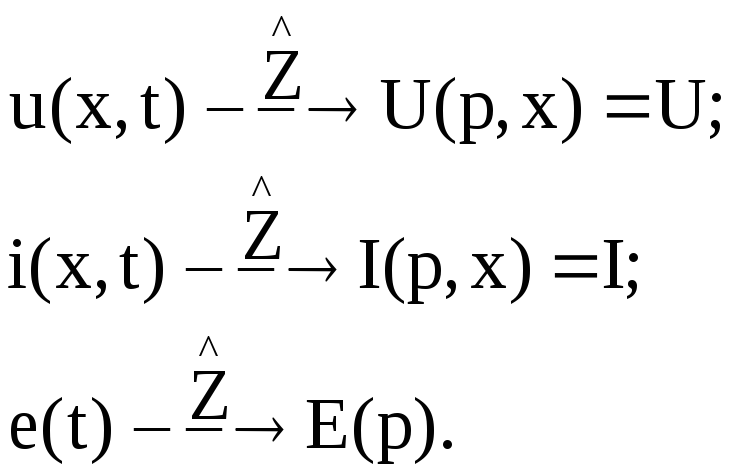(1.40)

Применяя преобразование Лапласа к системе уравнений получим систему операторных уравнений в полных производных:

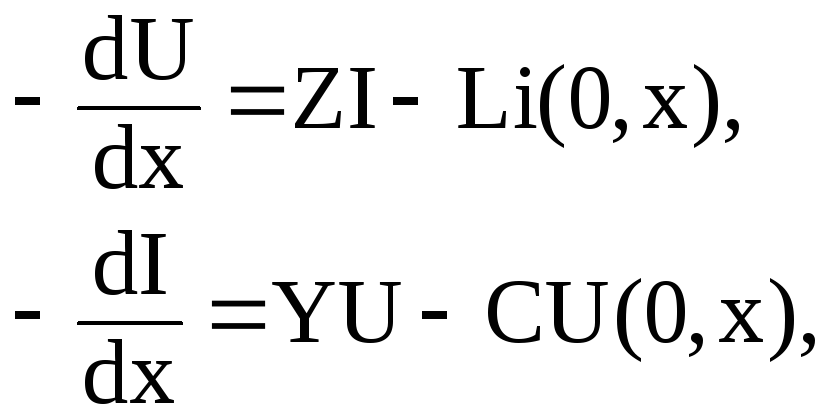(1.41)

где Z=pL+R; Y=рC+G. Если исключить одну переменную, тогда получим одно дифференциальное уравнение второго порядка:

(1.42)

где – операторная постоянная распространения волны; – функция начальных условий. Решение уравнения для U(x,p) состоит из общего решения однородного дифференциального уравнения и какого-либо частного решения U⁰:

U(p, x)= А₁(р) e^-γx+ A₂(р) e^γx +U⁰. (1.43)

Тогда из первого уравнения системы находим:

(1.44)

где - операторное волновое сопротивление; коэффициентыА₁(р) и A₂(р) определя­ются из граничных условий.

Решение операторной системы уравнений для изображения на­пряжения U(р,x) и тока I(р,x) найдено. Осуществив обратное преобразование Лапласа, восстанавливаем оригиналы на­пряжения U(x,t) и тока i(х,t). Однако решение в об­щем случае отыскать не удается. Рассмотрим некоторые частные случаи, для которых возможно нахождение решения.

Линия без потерь

В этом случае погонные параметры R=G=0 и . Тогда

(1.45)

Осуществляя обратное преобразование Лапласа, получим:

(1.46)

где

Следовательно, решение представляется в виде суммы прямой и обратной волны . Причем в данном случае амплитуда прямой и обратной волн не изменяется при их распространении вдоль линии.

Линия без искажений

Для данной линии характерно выполнение соотношения .Следовательно,

(1.47)

Изображение напряжения в линии есть

(1.48)

Осуществляя обратное преобразование Лапласа получим:

(1.49)

Следовательно, для линии без искажений мгновенные значения напряжения и тока представляют собой наложение прямой и обратной волн, затухающих в процессе распространения. Для линейных цепей с распределенными параметрами справедлив принцип наложения, следовательно, задачи анализа свободных и вынуж­денных колебаний могут рассматриваться порознь, аналогично це­пям с сосредоточенными параметрами.

Алгоритм решения задачи о собственных колебаниях в длинной линии

• определяем начальные условия

• записываем неоднородные дифференциальные уравнения (1.41) или (1.42) для конкретных начальных условий

• решаем неоднородное дифференциальное уравнение, находим частное решение неоднородного дифференциального уравнения

• находим общее решение дифференциального уравнения для изобра­жения напряжения U(x,р) и тока I(х,р)

• определяем коэффициенты А₁(р) и А₂(р) из граничных условий

• записываем решение для напряжения и тока в операторной форме (1.43) - (1.44)

• восстанавливаем оригиналы для напряжения и тока

• анализируем полученное решение

Пример 1.6. РАЗРЯД ОДНОРОДНОЙ ЛИНИИ БЕЗ ПОТЕРЬ

Исследовать разряд однородной линии без потерь (R=G=0), разомкнутой на конце через активное сопротивление .

Исследовать свободные колеба­ния в линии без потерь (рис.1.15).

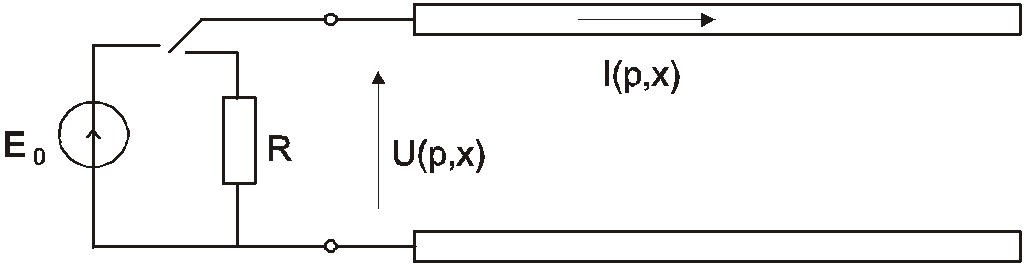
Рис.1.15. Длинная линия без потерь разомкнутая на конце

Для однородной длинной линии без потерь имеем

1) В соответствии с алгоритмом определяем начальные условия:

u(x,0)=E₀; i(x,0)=0.

Линия до начала исследования была заря­жена от источника постоянного напряжения до величины E₀. Ток через сопротивление отсутствовал.

2) Уравнение процесса для заданных начальных условий имеет вид (1.42):

3) Находим решение неоднородного дифференциального уравнения. Так как правая часть уравнения постоянная величина (не зависящая от х), то и частное решение неоднородного уравне­ния ищем в виде постоянной величины U⁰=const. Подставляя частное решение в уравнение, получаем:

-p²LCU⁰=-pLCE₀; тогда

4) Записываем общее решение операторного уравнения длинной линии:

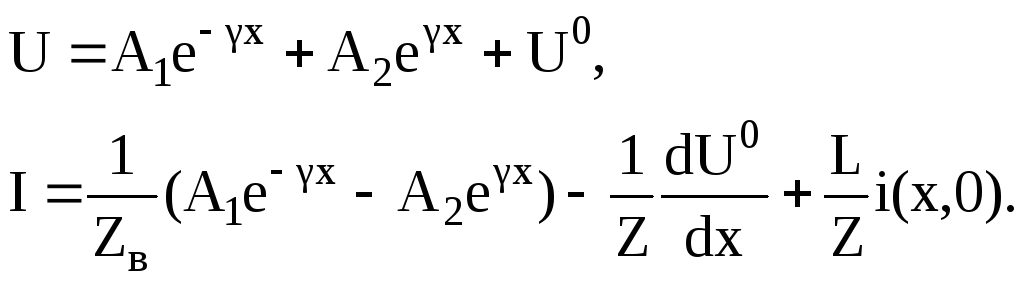
Подставляя найденное значение U⁰ и начальное значение для i(0,х), окончательно определяем:

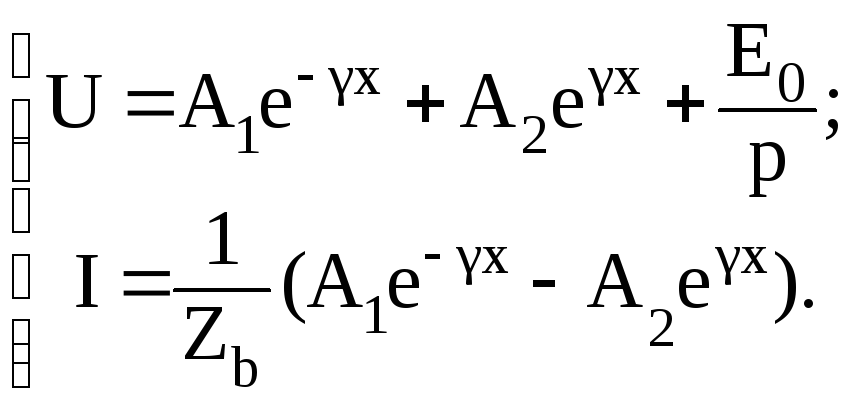
5) Используем граничные условия для определения коэффици­ентов A₁, и А₂. В начале линии выполняется следующее соотно­шение:

x=0, U(0,р)= -RI(0,р),

а так как в конце линия разомкнута, то при x=l получаем, что I(l,р)=0.

Следовательно, при x=0

поэтому

откуда находим при x=l:

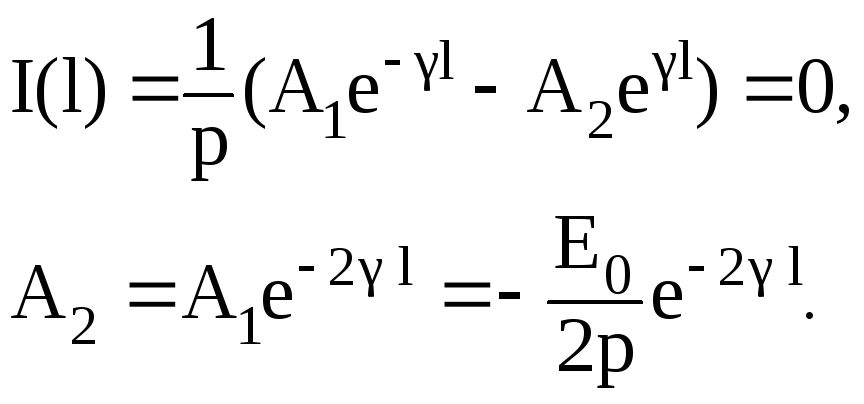
6) Записываем решение в операторной форме:

. Введем обозначение − время задержки сигнала, т.е. время, за которое сигнал доходит до конца линии.

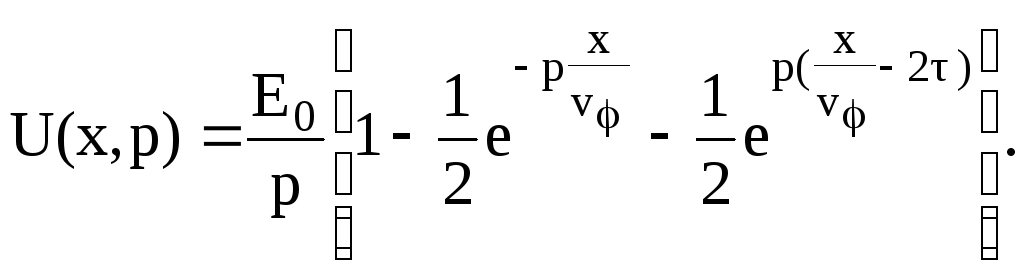
7) Восстанавливаем оригинал:

8) Анализируем полученный результат:

а) Определяем напряжение в сече­ниях x=0, и l.

В сечении x=0

.

В начале линии происходят следующие процессы: в начальный момент прямая волна распространяясь к концу линии, разряжает ее до величины 1/2 Е₀. Отразившись от конца линии она возвра­щается к началу линии и в момент времени равный 2τ разряжает ее до нуля. Поскольку время распространения прямой и обратной волн разряда линии равен 2τ, то в начале линии наблюдается прямоугольный импульс длительностью 2τ и амплитудой ½E₀ (рис.1.16).

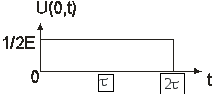
Рис.1.16. Закон изменения напряжения во времени в сечении х=0

б) Определим напряжение в сечении x=l/2 (рис.1.17).

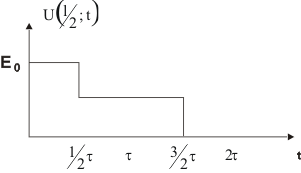В сечение х=l/2 прямая волна приходит в момент време­ни τ/2 и разряжает ее от значения амплитуды Е_о до амплитуды ½Е_о. В момент време­ни t=τ волна достигает конца линии и, отразившись, про­должает разряжать ее до нулевого значения (рис.1.17). В момент времени ⅔τ в сечении x=l/2 линия разрядится до нуля.

Рис.1.17 Закон изменения напряжения во времени в сечении x=l/2.

в) Определим напряжение в сечении x= l (рис.1.18).

Приx=l

На конце линии наблюдается импульс амплитудой E₀ и длитель­ностью τ, так как волна разряда достигает конца линии за вре­мя, равное τ (рис.1.18).

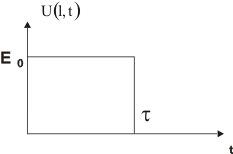
Рис.1.18. Закон изменения напряжения во времени в сечении x = l

г) Распределение напряжения в различные моменты времени (рис.1.19). Пусть, например, t=τ/2, тогда

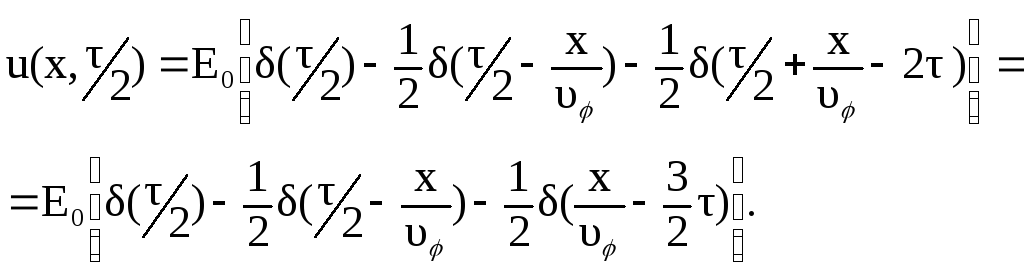
Первое слагаемое описывает постоянный уровень E_о, вто­рое слагаемое - прямую волну ступенчатой формы с амплитудой равной E_о/2, бегущую слева направо, третье слагаемое - обратную волну сту­пенчатой формы с амплитудой E_о/2, бегущую справа налево. В пре­делах длины линии 0<x<l наложение этих волн описывает про­цесс разряда линии (рис.1.19).

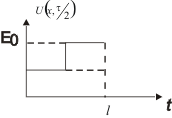
Рис.1.19. Распределение напряжения вдоль длинной линии во времени