§2.11.3. Метод вкб (Вентцеля-Крамера-Бриллюэна)

Метод предназначен для нахождения приближенных решений дифференциальных уравнений второго порядка с переменными коэффициентами вида:

(2.120)

- уравнение Хилла, причем на функцию F(t) накладывается ряд ограничений.

При определенном подходе к анализу параметрических цепей, в ряде случаев последние могут быть представлены соединением простых цепей, каждая из которых описывается дифференциальными уравнениями порядка не выше второго.

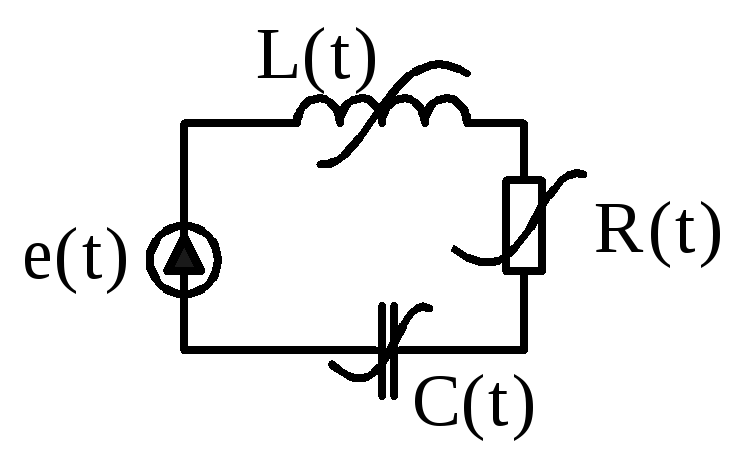
В общем случае такой цепью является одноконтурная цепь, содержащая все элементы с переменными характеристиками (рис.2.39). Уравнение цепи запишем в виде:

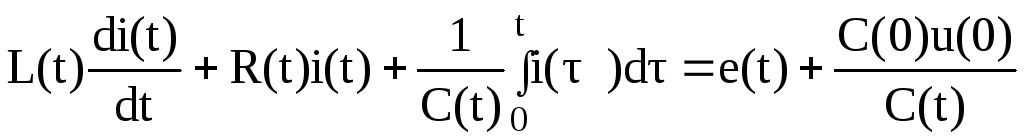(2.121)

Рис.2.39. Параметрическая цепь, состоящая из всех параметрических

элементов

Нахождение колебаний в цепи (рис.2.39) мы разобьем на три этапа. На первом этапе приведем уравнение (2.121) к уравнению Хилла (2.120). Затем воспользуемся методом ВКБ для построения однородного уравнения Хилла. На последнем, третьем этапе, построим решение неоднородного уравнения Хилла известным методом вариации постоянных составляющих.

Первый этап. Мы получили интегродифференциальное уравнение вида (2.121). Для того, чтобы получить дифференциальное уравнение второго порядка, сделаем замену переменных

. (2.122)

Подставим выражение (2.122) в уравнение (2.121):

,

где f(t) = e(t) + ,

или , где. (2.123)

В последнем уравнении сделаны следующие обозначения коэффициентов:

2δ(t) = , .

Сделаем замену переменной и найдем первую и вторую производные для q(t):

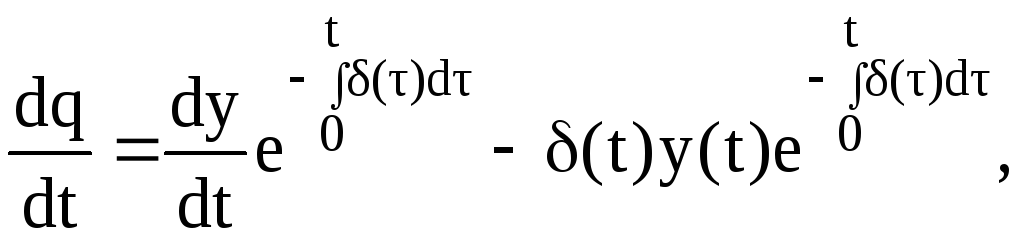
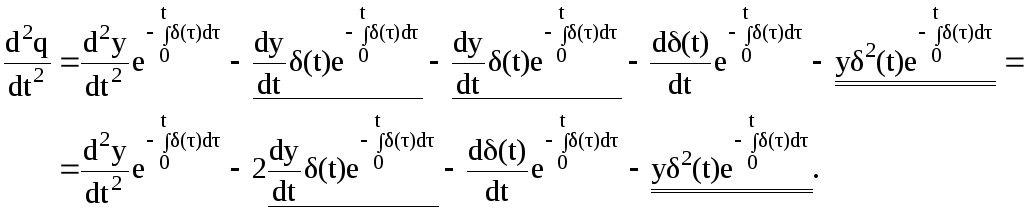После подстановки полученных производных в уравнение (2.123) получим:

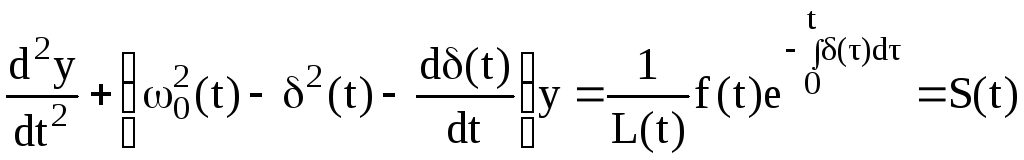. (2.124)

Обозначим коэффициент, стоящий в скобках в уравнении (2.124) через F(t)

, где . (2.125)

Мы показали, что колебания в одноконтурной параметрической цепи (рис.2.34), описываются неоднородным уравнением Хилла.

Второй этап. Решение однородного уравнения Хилла (2.120):

(2.126)

находится с помощью метода ВКБ. Для того, чтобы возможно было применить метод ВКБ, функция F(t) должна удовлетворять следующему условию:

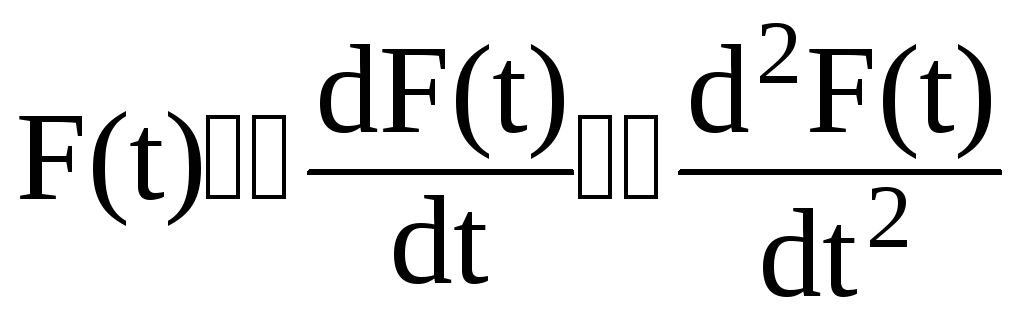(2.127)

(медленное изменение F(t)). Так как у нас учебный процесс, то для построения решения однородного дифференциального уравнения Хилла потребуем, чтобы выполнялось следующие условие. Пусть

, т.е. F(t)>0 (2.128)

(это требование не обязательно в методе ВКБ, однако оно позволяет избежать исследования разветленных решений).

Ищем решение однородного уравнения Хилла (2.126) в виде следующей функции

. (2.129)

Тогда находим, что

. (2.130)

Подставляя соотношения (2.129-2.130) в уравнение (2.126) получим:

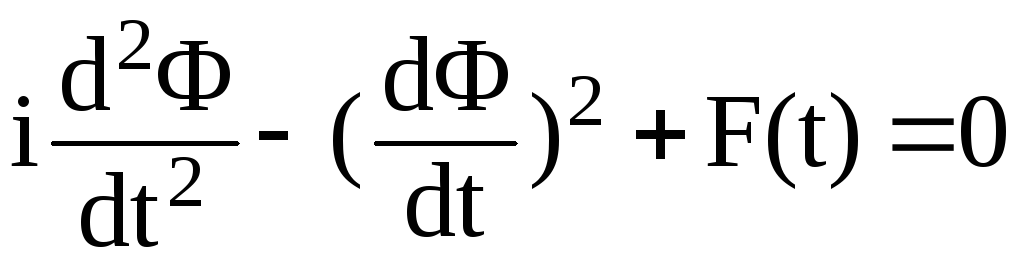. (2.131)

Полученное уравнение является неоднородным, решить которое труднее чем исходное (2.126). Однако, если мало, можно использовать метод итераций (приближений). Запишем уравнение (2.129) в следующем виде

. (2.130)

Так как у нас выполняется условие (2.127), то можно пренебречь вторым слагаемым в правой части уравнения (2.130), так как у нас решение является медленно меняющейся функцией. А это значит, что .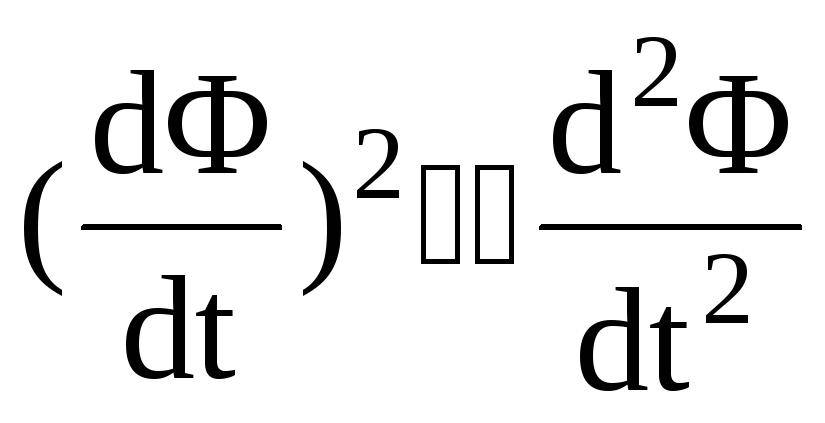

Тогда нулевое приближение находим из уравнения

. (2.131)

С учетом условия (2.128), мы можем уравнение (2.131) записать в виде:

. (2.132)

Если бы не выполнялось условие (2.128), нам пришлось бы для отрицательных значений коэффициента F(t)<0 найти дополнительное решение уравнения вида:

,

что не вызывает трудностей, однако делает построение решения более громоздким.

Дифференциальное уравнение (2.132) является уравнением с разделяющимися переменными, поэтому решение его имеет вид:

. (2.133)

При построении решения уравнения (2.130) мы пренебрегли вторым слагаемым в правой части уравнения. Для проверки законности данного действия давайте найдем вторую производную функции и сравним ее с коэффициентомF(t). Для того чтобы найти вторую производную функции можно два раза продифференцировать выражение (2.133), либо один раз выражение (2.132). Выполняя дифференцирование функции , находим:

.

Поэтому условием применимости построения нулевого приближения (нулевой итерации) как решения укороченного уравнения (2.131) есть выполнение неравенства:

(2.134)

Для нахождения первого приближения (первой итерации), заменим второе слагаемое в правой части уравнения (2.130), используя найденное нулевое приближение функции Ф(t). Тогда правая часть уравнения (2.130) будет выражаться через известные функции, а уравнение для нахождения первого приближения примет вид:

. (2.135)

Найти стогое решение уравнения (2.135) в общем виде не удается, однако учитывая выполнение условия (2.134), разложим правую часть уравнения (2.135) в ряд Тейлора и пренебрежем слагаемыми выше первого порядка малости:

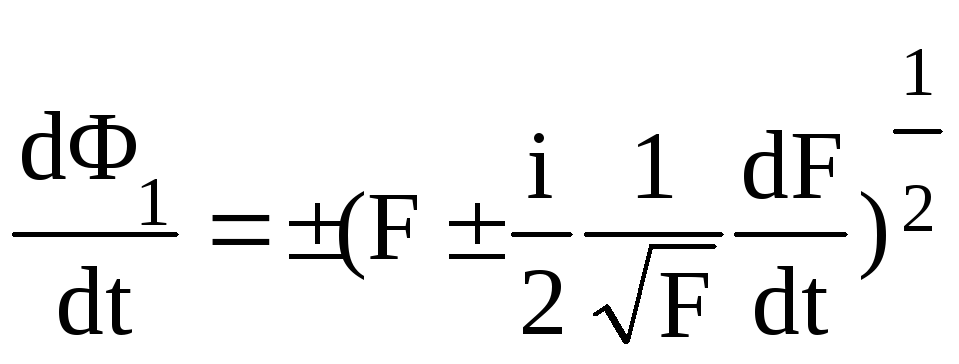, (2.136)

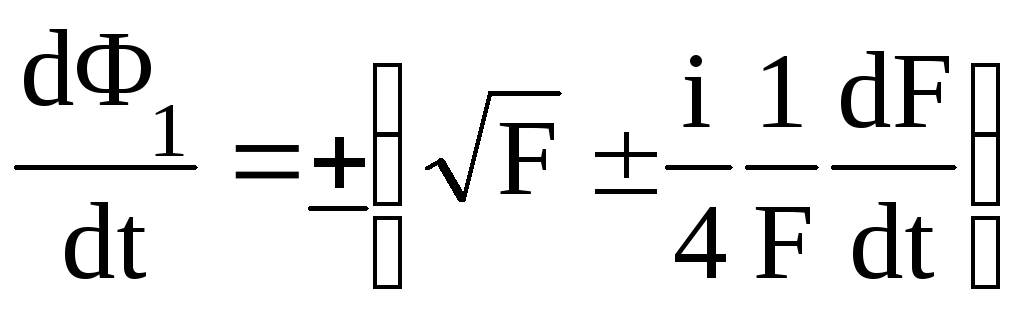(2.137)

(правая часть уравнения (2.137) записана с использованием разложения в ряд Тейлора функции и пренебрежением всеми слагаемыми выше первого порядка малости). При раскрытии скобок в правой части уравнения (2.137) возможно выбрать у второго слагаемого знак, как плюс, так и минус. Мы запишем знак плюс и после получения решения нашего уравнения (2.121) сделаем переход к известному результату для колебательного контура с постоянными параметрами. Что позволит доказать правильность выбранного знака второго слагаемого в выражении (2.138)

. (2.138)

Решая уравнение (2.138) получаем первое приближение для функции Ф(t)

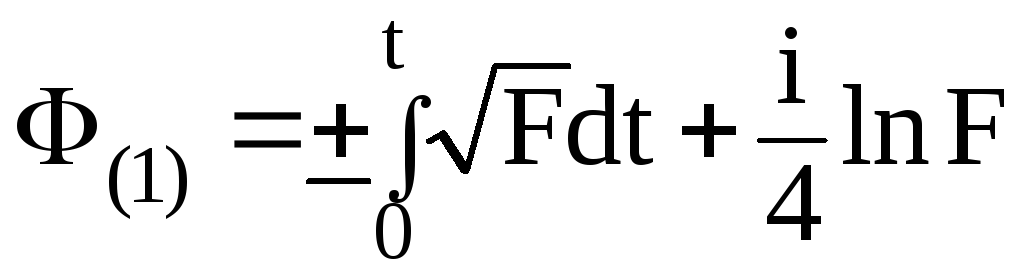. (2.139)

Получим условия возможности применения уравнения (2.138) для построения первого приближения. Для этого, используя решения (2.138) или (2.139), найдем и сравним ее с F(t):

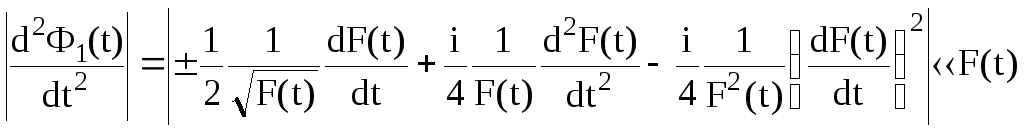. (2.140)

Условия (2.134) и (2.140) позволяют, до начала построения решения однородного уравнения Хилла с помощью известной функции F(t) проверить возможность построения приближений с помощью метода ВКБ.

Процесс построения приближений (итераций) можно продолжить до любого порядка точности как решение уравнения (2.141):

, (2.141)

но мы ограничимся первым приближением. Подставим выражение (2.139) в (2.129) и найдем, что две функции y₁(t) и y₂(t) являются решением уравнения Хилла:

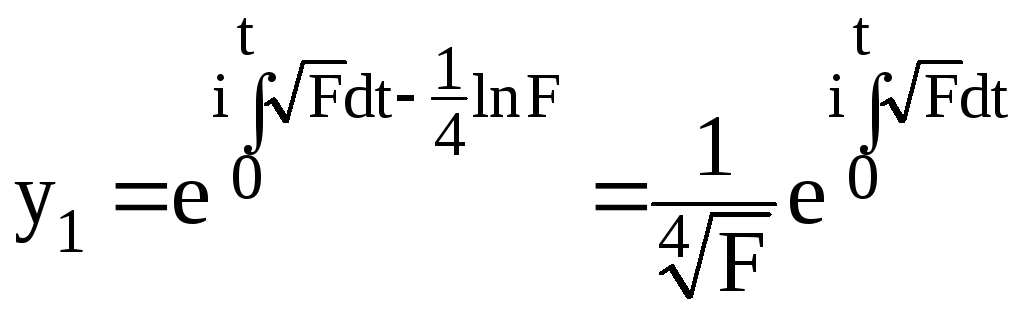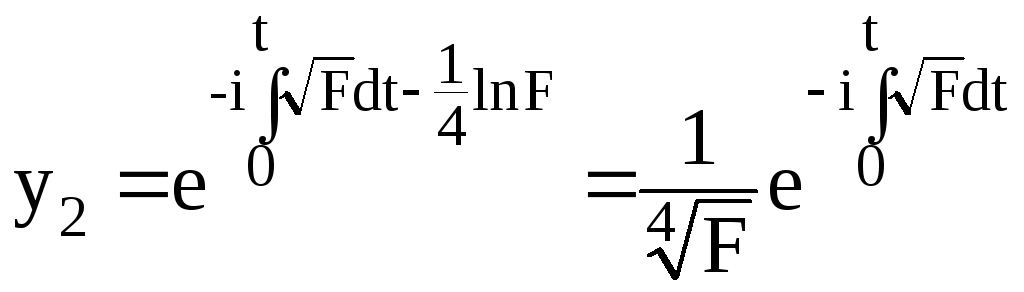и . (2.143)

Следовательно, окончательно можем записать решение уравнения Хилла в виде суммы двух слагаемых:

y(t)=u₁y₁(t) + u₂y₂(t). (2.144)

Третий этап. Решение неоднородного уравнения Хилла

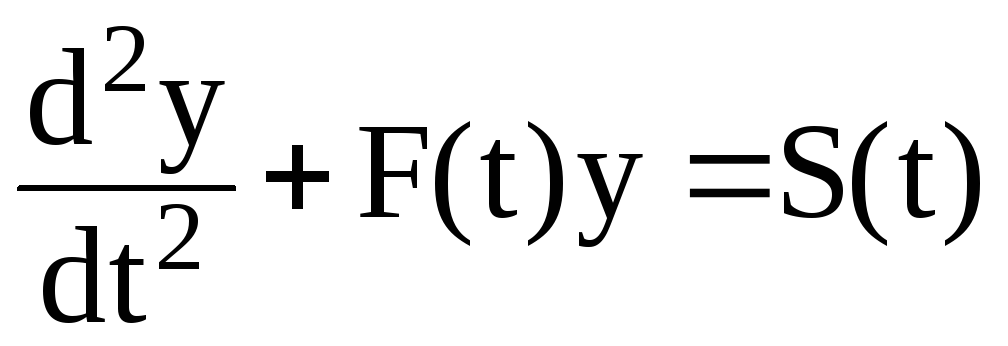(2.145)

можно находить методом вариации произвольных постоянных. Поэтому, используя метод вариации произвольных постоянной (метод Лагранжа), решение ищем в виде:

, (2.146)

где и- некоторые неизвестные коэффициенты.

Найдем первую производную

.

При произволе выбора коэффициентов потребуем, чтобы выполнялось условие

, (2.147)

тогда вторая производная

.

Подставим найденные первую и вторую производные в основное уравнение (2.145) и найдем

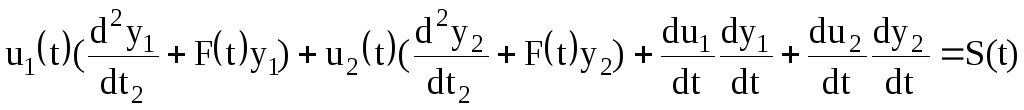. (2.148)

В уравнении (2.148) в скобках стоят выражения тождественно равные нулю, т.к. функции y₁(t) и y₂(t) являются решениями однородного уравнения Хилла (2.126). Поэтому мы получили систему из двух уравнений для двух неизвестных коэффициентов u₁(t) и u₂(t):

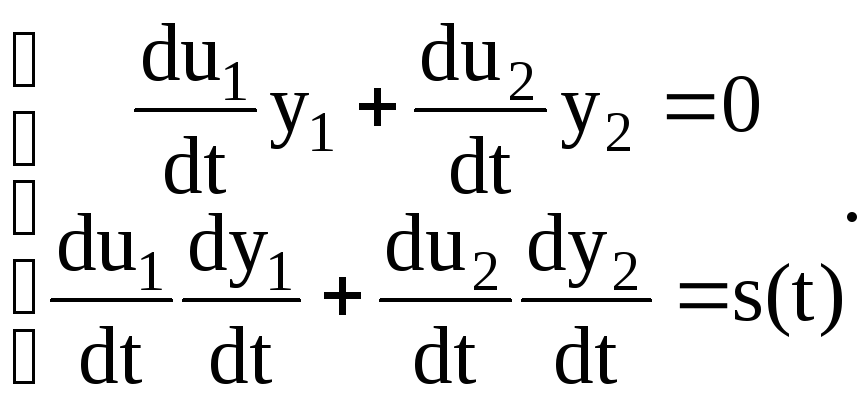(2.149)

Таким образом, имеем систему уравнений относительно 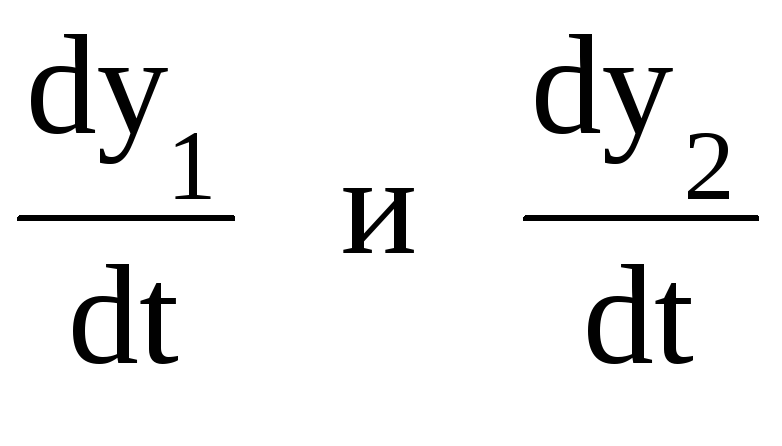матричная форма, которой имеет вид:

. (2.150)

Решение системы уравнений (2.150) или (2.149) можно записать в виде:

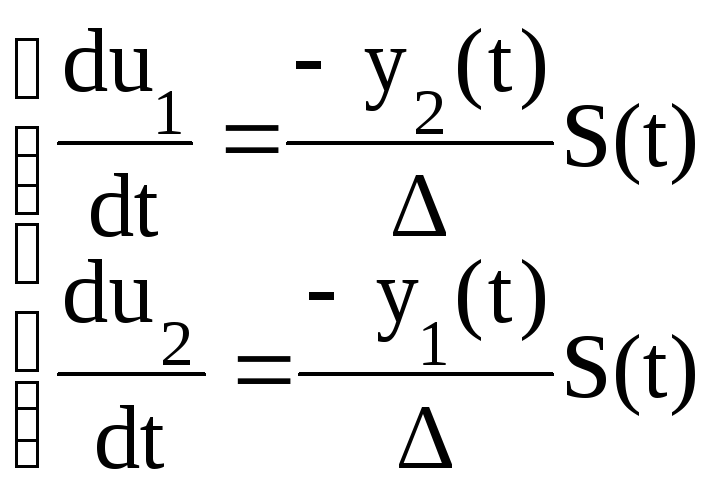
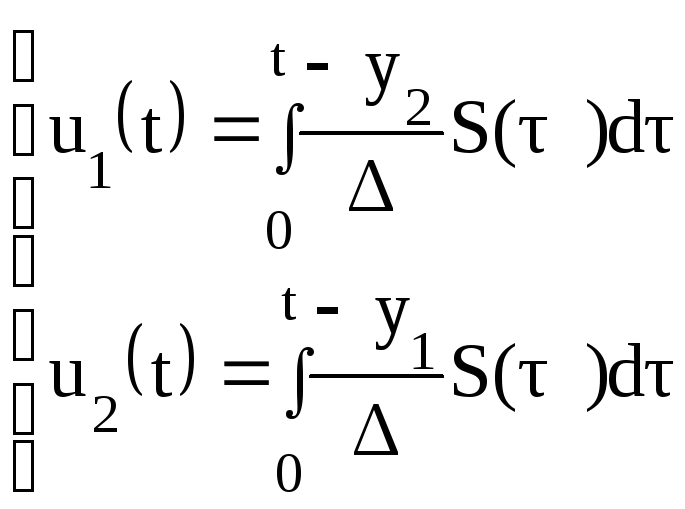. (2.151)

Дальнейшее рассмотрение решения неоднородного уравнения Хилла в общем виде невозможно, поэтому конкретизируем вид входного сигнала. Будем считать, что входной сигнал представлен в виде короткого импульса с амплитудой U₀

, тогда 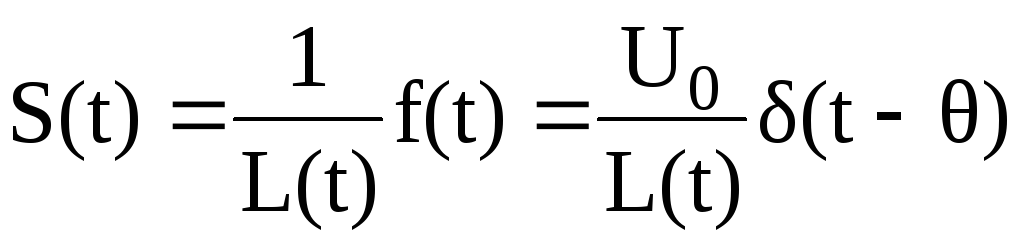. (2.152)

Подставляя S(t) в решение (2.151) найдем выражение для неизвестных коэффициентов u₁ и u₂:

, а , (2.153)

Подставляя найденные методом вариации произвольной постоянной коэффициенты (2.153) в решение (2.146) найдим

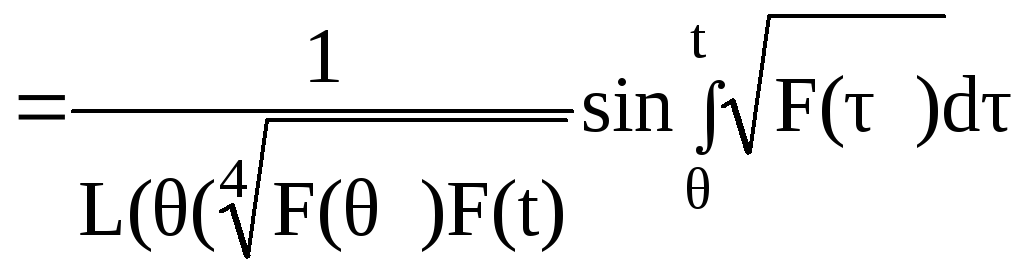. (2.154)

При выводе решения (2.154) учтено, что .

Возвращаясь к переменной , найдем

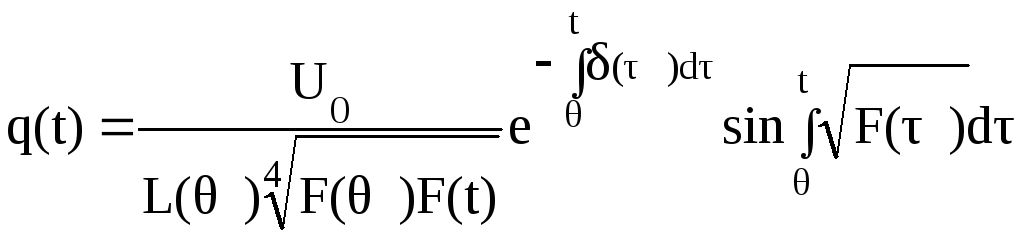. (2.155)

Для того чтобы проверить правильность полученного выражения, сделаем переход к колебательному контуру содержащему все постоянные элементы. Напомним, что , тогда переходя к постоянным значениям, получаем следующий результат:

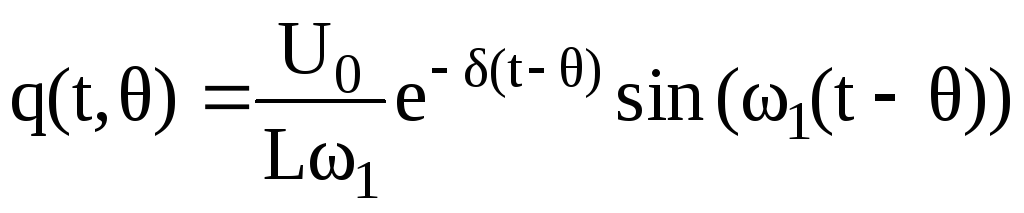, а . (2.156)

Хорошо известный результат, полученный при исследовании колебаний в контуре с постоянными элементами (см. пример 1.1). Колебания в нем являются экспоненциально затухающими гармоническими с постоянной частотой ω₁. Таким образом, можно сделать вывод, что все сделанные нами допущения единственно правильные. Метод ВКБ позволил определить закон изменеия напряжения, тока и заряда в контуре у которого все элементы являются параметрическими.