§3.2 Аппроксимация характеристик нелинейных элементов

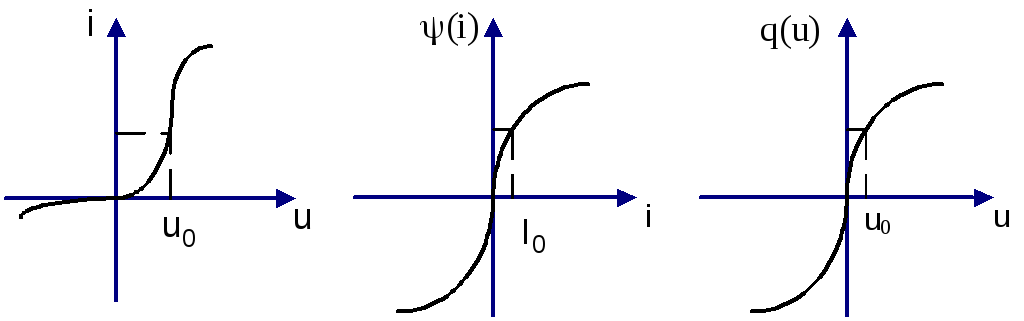
Как указывалось ранее, удобными характеристиками нелинейных элементов являются не уравнения связи, а вольтамперная характеристика активного сопротивления или, или зависимость- для нелинейной индуктивности (ампервеберная характеристика), или зависимостьq(u) – для нелинейной емкости (вольткулонная характеристика) (рис.3.8).

Рис.3.8. Виды характеристик нелинейных элементов

Однако, графическая форма характеристик нелинейных элементов (рис.3.8.) не позволяет использовать зависимости (3.1-3.15), для составления уравнений работы схем с нелинейными элементами. Поэтому одной из важнейших задач, которая возникает при анализе колебаний в схемах, содержащих нелинейные элементы, состоит в аппроксимации нелинейных характеристик. Наибольшее распространение аппроксимаций нелинейных характеристик получили полиномиальная и кусочно-линейная, а также аппроксимация с помощью различных видов трансцендентных функций.

При анализе нелинейных схем возможность получить правильный результат существенно зависит как от правильности выбора метода аппроксимации, так и от выражения аппроксимирующей функции нелинейного элемента. Возникает определенное противоречие – чем точнее аппроксимация нелинейного элемента, тем сложнее получить нужное аналитическое выражение характеристики нелинейного элемента. Но кроме этого, сложнее построить и решение нелинейного уравнения, описываюшего колебания в такой нелинейной системе, с помощью выбранного выражения аппроксимирующей функции. Поэтому правильный выбор аппроксимации нелинейной характеристики позволяет существенно упростить построение решения нелинейного уравнения. Кроме того необходимо отметить, что очень часто одну и ту же характеристику нелинейного элемента приходится по-разному аппроксимировать в зависимости от того, в каких условиях работает нелинейный элемент и какие вопросы должны быть исследованы. Поэтому, способы аппроксимации выбирают в каждом конкретном случае исследования колебаний в схемах с нелинейными элементами различными.

Рассмотрим способы аппроксимации различных функций нелинейных элементов. К наиболее распространенным способам аппроксимации нелинейных элементов относят следующие:

• полиномиальная аппроксимация ─ представление нелинейной характеристики с помощью степенного ряда,

• кусочно-линейная аппроксимация ─ представление аппроксимируемой функции отрезками прямых линий,

• аппроксимация с помощью различных видов трансцендентных функций.

Полиномиальная аппроксимация. Если любая из нелинейных характеристик задана аналитическим выражением, то в окрестности рабочей точки функция может быть представлена разложением в ряд Тейлора (в окрестности точки х₀)

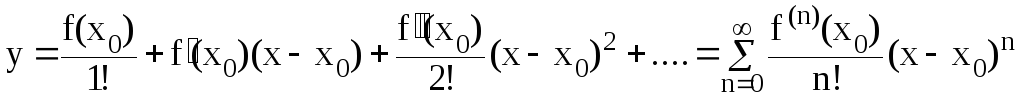
или

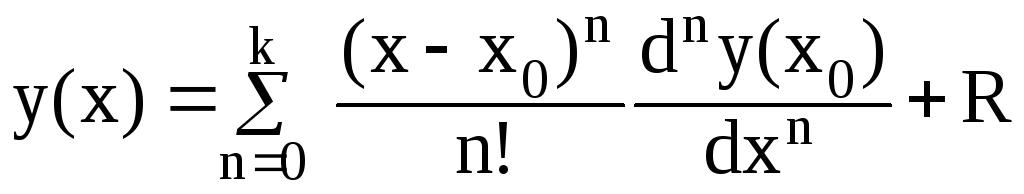, (3.16)

где R – остаток в разложении в ряд Тейлора, которым пренебрегают при аппроксимации.

Если же характеристика задана графически (рис.3.9), то аппроксимацию можно осуществить укороченным степенным рядом (полином), ограничивая его второй - пятой степенью

. (3.17)

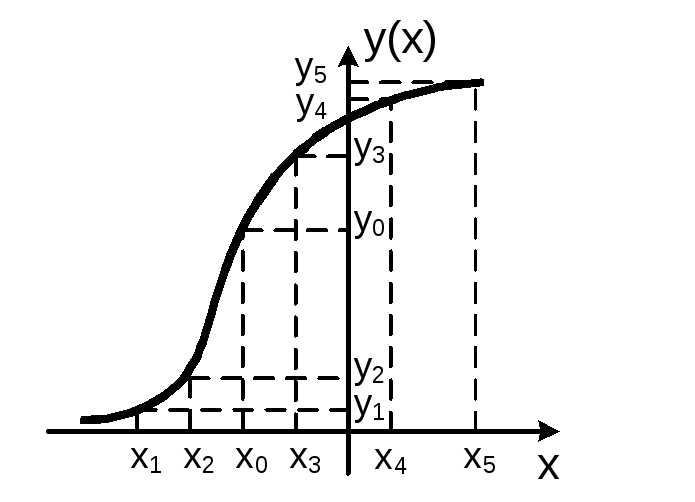
Рис.3.9. Графическое представление нелинейной характеристики

Для определения коэффициентов а_k требуем, чтобы при значениях переменной x_k в левой части полинома (3.17) получались значения функции y_k.

Составляем систему уравнений:

, где . (3.18)

В этой системе уравнений y_n, у₀, x_n, x₀ – известные величины, поэтому эту систему можно решить по методу Крамера, относительно коэффициентов a_k.

Если x=x₀+S (х₀ постоянное смещение, а S малый сигнал), то

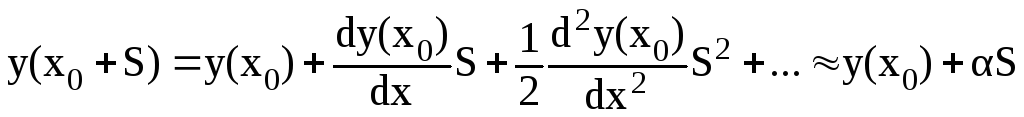, (3.19)

где α – дифференциальный параметр нелинейного элемента. Таким образом, можно отметить, что первый коэффициент a₁ полиномиальной аппроксимации нелинейной характеристики (3.17) совпадает с дифференциальным параметром нелинейного элемента. Кроме того отметим, что если х=0 лежит внутри интервала (х₅-х₁) аппроксимации нелинейной характеристики полиномом, то коэффициент а₀ определяет значение функции в начале координат (т.е. если мы рассматриваем в качестве нелинейной характеристики i=φ(u), то коэффициент а₀=i(0) определяется как значение тока при u=0.

Кусочно-линейная аппроксимация. Кусочно-линейная аппроксимация основана на замене реальной характеристики нелинейного элемента отдельными участками, которые заменяются отрезками прямых линий (рис.3.10).

Рис.3.10. Кусочно-линейная аппроксимация нелинейного элемента

Точность кусочно-линейного приближения зависит от количества интервалов, заменяемых отрезками прямых в заданном интервале использования кусочно-линейной аппроксимации. Чем на большее количество отрезков прямых разбит интервал, для которого мы применяем кусочно-линейное приближение, тем выше точность совпадения с реальной нелинейной характеристикой, но при этом сушественно усложняется анализ колебаний в такой системе. Для упрощения расчетов желательно ограничиваться минимальным количеством отрезков прямых, замещающих нелинейную характеристику. Например, динамическую проходную характеристику триода (рис.3.10) можно аппроксимировать с достаточной степенью точности всего лишь тремя отрезками прямых линий:

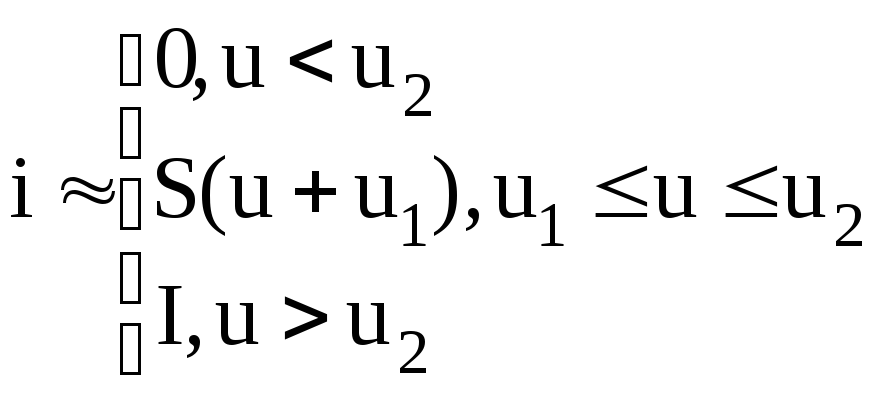. (3.20)

Замена нелинейных участков характеристик нелинейных элементов отрезками прямых, прозволяет считать и сами характеристики линейными, а это значит, что применимы теперь все методы линейной теории цепей. На протяжении линейных участков нелинейные элементы заменяются на линейные, с характеристиками равными их дифференциальным величинам.

Аппроксимация нелинейных характеристик с помощью трансцендентных функций. Иногда характеристики нелинейных элементов аппроксимируют трансцендентными функциями рис.3.11. В качестве аппроксимирующих трансцендентных функций применяются экспоненты и их суммы, тригонометрические, обратные тригонометрические, гиперболические и другие функции. Например,

или . (3.21)

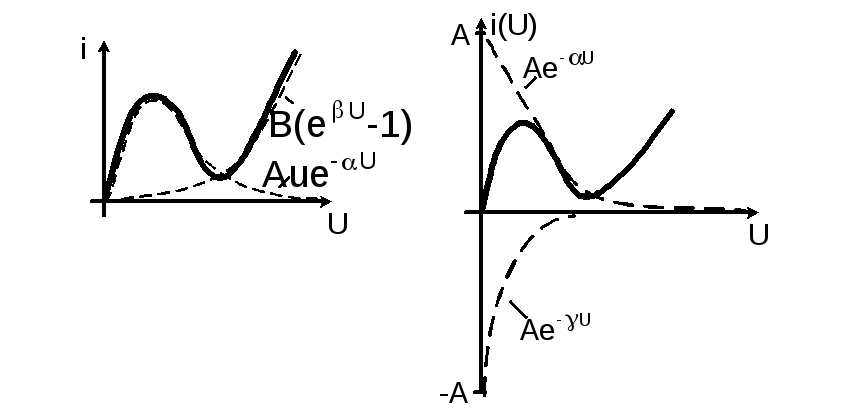
Рис.3.11. Примеры аппроксимации нелинейных характеристик

трансцендентными функциями