§2.11. Некоторые приближенные методы исследования процессов в параметрических системах

§2.11.1. Метод «замороженного» параметра

Метод «замороженного» параметра − простейшая разновидность методов «заморожевания переменных». Идея этих методов заключается в следующем: в заданном дифференциальном уравнении выделяется одна переменная (или комбинация переменных) и ее значение фиксируется «замораживается». При фиксированном значении переменной ищется решение дифференциального уравнения, после этого фиксируется новое значение переменной и ищется новое решение и т.д. Множество найденных решений дифференциального уравнения, при добавлении заданных начальных условий, позволяет построить искомое решение. В качестве «замораживаемых» могут быть: зависимые переменные, независимые переменные, коэффициенты уравнений, а также различные комбинации переменных.

Рассмотрим применение данного метода для исследования параметрических колебательных систем. В качестве «замораживаемых» переменных здесь выступают коэффициенты дифференциальных уравнений. Как известно, коэффициентами дифференциальных уравнений выступают элементы радиотехнических цепей (сопротивления, индуктивность, емкости и т.д.). Поэтому, для того чтобы было возможно применять метод «замороженного» параметра (т.е. считать параметры постоянным на протяжении какого-то интервала времени), необходимо потребовать выполнения следующего условия: изменение этих коэффициентов – параметров, происходит очень медленно по сравнению с характерным изменением колебаний в парметрической цепи.

Пусть у нас имеется параметрическая цепь (рис.2.32). На вход нашей параметрической цепи подается либо входной сигнал S_вх(t) и нам необходимо найти отклик в виде S_вых(t), либо воздействие в виде короткого импульса

Рис.2.32. Параметрическая цепь

S_вх(t)=δ(t - θ) и нам необходимо найти отклик в виде импульсной функции цепи. Пусть, например, для составления системы уравнений нам удобней применять метод контурных токов. Выберем систему независимых контуров, направления их обхода, и запишем с помощью МКТ следующую систему уравнений:

. (2.96)

Полагаем , т.е. полагаем значение элементов постоянными - «замороженными» и решаем полученную систему уравнений с постоянными коэффициентами:

.

Применяем преобразование Лапласа к полученной системе уравнений с постоянными коэффициентами. Если все функции, преобразуемы по Лапласу, получаем

.

Решение последнего уравнения записываем, используя формулы (1.24 – 1.25)

где b=b(R, G, L, C); a=a(R, G, L, C) , р_k=р_k(R, G, L, C).

«Размораживаем» параметры, т.е. полагаем, что они стали функциями времени t, следовательно, коэффициенты a=a(R, G, L,C), b=b(R, G, L, C) и р_k=р_k(R, G, L, C) становятся также функциями времени t, т.е. b=b(t), a=a(t) и корни р_k=р_k(t). Поэтому окончательно получаем для S_вых следующее выражение:

S_вых = =

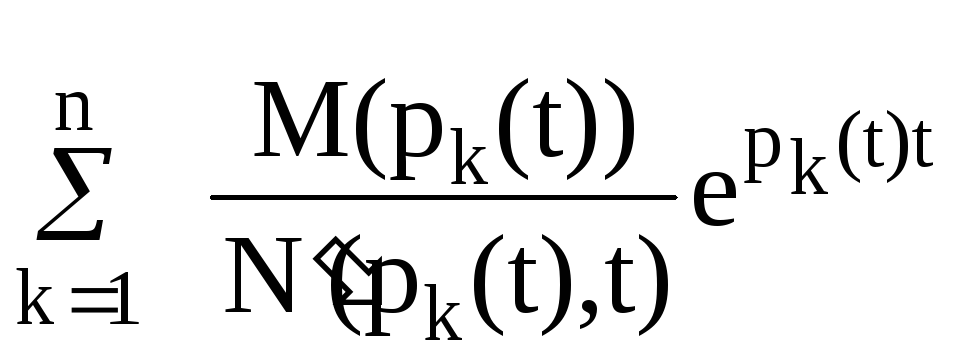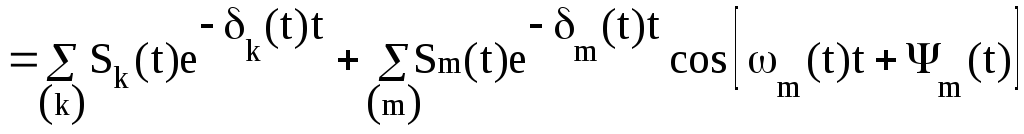. (2.98)

Определяем импульсную функцию для случая m<n.

,

Рис.2.33. Характер изменения импульсной передаточной функции