
- •Министерство образования и науки украины
- •Введение
- •Глава і Свободные и вынужденные колебания в линейных инвариантных динамических системах
- •§1.1.Преобразование Лапласа и его основные свойства
- •§ 1.2. Применение операторного метода для анализа процессов в цепях с сосредоточенными элементами
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях
- •§1.4 Общий вид решения задачи анализа прохождения сигнала через устойчивую линейную цепь
- •Алгоритм решения задач анализа вынужденных колебаний в электрических цепях
- •§1.5. Свободные колебания в динамических системах с распределенными элементами
- •§1.5.1. Классификация длинных линий
- •§1.5.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •Глава іі Колебания в линейных параметрических системах Линейные параметрические цепи
- •§ 2.1. Изменение спектра входного сигнала при прохождении через линейные параметрические цепи
- •§ 2.2. Аксиоматика теории цепей в параметрическом случае
- •§2.3. Прохождение сигналов через параметрические r – цепи
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с одной степенью свободы. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.5.1. Процессы в механической параметрической колебательной
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.6. Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье
- •§ 2.7. Параметрическое усиление колебаний в одноконтурной системе. Синхронный режим. Асинхронный режим
- •§2.8. Параметрический генератор (параметрон)
- •§2.9. Двухконтурные параметрические системы
- •§2.9.1.Теорема Менли-Роу
- •§2.9.2 .Двухконтурный параметрический усилитель нерегененративного типа
- •§2.9.3 .Двухконтурный параметрический усилитель регененративного типа
- •§ 2.9.4 Параметрические умножение и деление частоты
- •§2.11. Некоторые приближенные методы исследования процессов в параметрических системах
- •§2.11.1. Метод «замороженного» параметра
- •§2.11.2. Алгоритм метода замороженного параметра для задачи о свободных и вынужденных колебаниях в параметрических цепях
- •§2.11.3 Метод последовательных приближений
- •§2.11.3. Метод вкб (Вентцеля-Крамера-Бриллюэна)
- •Глава ш Анализ колебаний в нелинейных цепях
- •§3.1. Нелинейные элементы цепей
- •§3.2 Аппроксимация характеристик нелинейных элементов
- •§3.3 Преобразование спектра колебаний нелинейной цепью
- •§3.4 Особенности задач анализа колебаний в нелинейных цепях
- •§3.5 Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений
- •§3.6. Метод линеаризации
- •§3.7. Метод гармонической линеаризации (мгл)
- •§3.7.1. Эквивалентные параметры нелинейных элементов
- •§3.7.2. Автогенератор гармонических колебаний.
- •§3.8. Методы малого параметра. Метод последовательных приближений
- •§3.9. Метод медленно меняющихся амплитуд (ммма).
- •§3.10. Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде
- •§3.11. Метод фазовой плоскости
- •§3.11. 1.Метод фазовой плоскости. Метод изоклин
- •§3.11.2. Метод фазовой плоскости. Особые точки
- •§3.11.2.Исследование методом фазовой плоскости схемы на
- •§1.1. Преобразование Лапласа и его основные свойства 7
- •610077,М. Харків, пл. Свободи, 4.
- •610077,М. Харків, пл. Свободи, 4.
§ 2.7. Параметрическое усиление колебаний в одноконтурной системе. Синхронный режим. Асинхронный режим
В предыдущем разделе был найден закон изменения заряда (2.65), тока и напряжения (2.66) в одноконтурном параметрическом усилителе методом сведения уравнения (2.56), описывающего колебания в такой цепи к неоднородному уравнению Матье (2.60). Однако, полученное решение, кроме того что выражается через специальные функции Матье, не позволяет определить многие важные характеристики цепи, такие как коэффициент усиления, добротность и т.д. Поэтому для определения этих характеристик пользуются другими методами. Кроме того отличают два режима работы одноконтурных параметрических усилителей: синхронный режим и асинхронный режим. Различие данных режимов работы параметрических усилителей заключается в следующем:
синхронный режим возникает в параметрическом усилителе, когда строго выполняется соотношение между частотой накачки ωн = Ω и частотой усиливаемого сигнала ωс
ωн = 2ωс; (2.67)
асинхронным называется режим, при котором строгое равенство (2.67) нарушается из-за невозможности настроить частоты друг на друга в точности, а соотношение между ними может быть записано в следующем виде
2ωс = ωн + η, где η « 1. (2.68)
Рассмотрим
синхронный
режим работы
параметрического усилителя. Найдем
основные характеристики одноконтурного
параметрического усилителя, работающего
в синхронном режиме. Пусть у нас имеется
источник внешнего сигнала - гармоническое
колебание
![]() .
В сопротивление
.
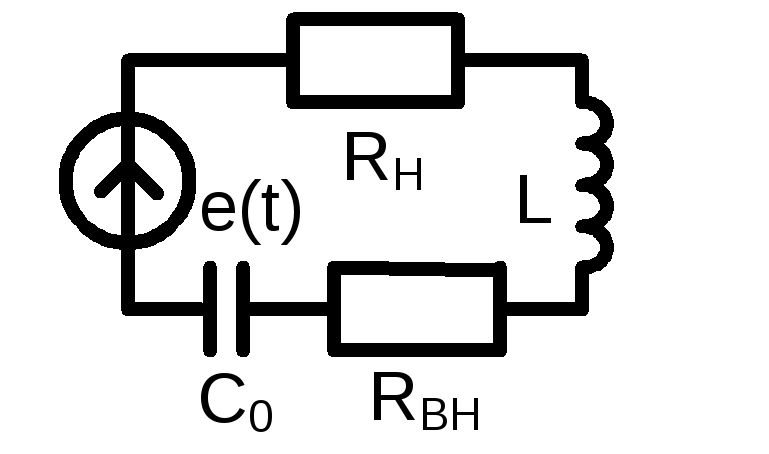
В сопротивление![]() (рис.2.17) входит сопротивление генератора
и сопротивление катушки индуктивности.
Рассмотрим колебания в одноконтурной
параметрической системе. Пусть частота
сигнала равна частоте
(рис.2.17) входит сопротивление генератора
и сопротивление катушки индуктивности.
Рассмотрим колебания в одноконтурной
параметрической системе. Пусть частота
сигнала равна частоте

Рис.2.17. Одноконтурный параметрический усилитель
резонанса контура
![]() .
(2.69)
.
(2.69)
Будем
считать, что параметры контура такие,
что мы попадаем в первую зону неустойчивости
рис.2.16., т.е.
![]() .
Тогда
.
Тогда
![]() и
пусть
и
пусть
![]() .
(2.70)
.
(2.70)
Считаем, что добротность колебательного контура велика, тогда отклики на входной сигнал, которые возникнут в параметрическом колебательном контуре, будут близкими к гармоническим колебаниям. Это позволяет нам для анализа колебаний использовать метод комплексных амплитуд (МКА). Поэтому мы можем записать
![]() .
.
При
резонансе напряжение на индуктивности
в Q
раз
превышает
амплитуду напряжения источника
![]() .
По определению добротностьQ
равна
.
По определению добротностьQ
равна
![]() ,
(2.71)
,
(2.71)
где![]() -
вносимое сопротивление, которое описывает
энергию, вносимую в колебательный контур
вследствие того, что ёмкость является
параметрической. Используя аксиоматику
цепей для параметрической емкости
(2.11) запишем
-
вносимое сопротивление, которое описывает
энергию, вносимую в колебательный контур
вследствие того, что ёмкость является
параметрической. Используя аксиоматику
цепей для параметрической емкости
(2.11) запишем
![]() .
.
Первое слагаемое в этом соотношении – обычное емкостное слагаемое, свидетельствующее о том, что линейная постоянная емкость запасает и расходует энергию. Второе – аналогично выражению для мощности, расходуемой на каком-то постоянном сопротивлении. Вычислим среднюю мощность, вносимую в колебательный контур параметрической емкостью:
![]() .
(2.72)
.
(2.72)
Для того чтобы вычислить эту мощность необходимо задать закон изменения заряда q(t). В предыдущем разделе мы нашли, что закон изменения заряда может быть записан, в виде
![]() ,
,
здесь ни затухания, ни нарастания нет, т.к. нам необходимо определить коэффициент модуляции mкр, характеризующий стационарные колебания (т.е. колебания с постоянной амплитудой). Напряжение и ток определяются из следующих формул:
![]() .
.
Подставляя
выражение для
![]() ,U(t)
и i(t)
в (2.72), после несложных преобразований
находим, что
,U(t)
и i(t)
в (2.72), после несложных преобразований
находим, что
![]() .
(2.73)
.
(2.73)
Эта
величина имеет известный вид
![]() и равна мощности, которая расходуется
на активном постоянном сопротивлении.
и равна мощности, которая расходуется
на активном постоянном сопротивлении.
 Всё,
что стоит в скобках в выражении (2.73)
можно обозначить через вносимое
сопротивление. Поэтому энергию, вносимую
параметрической ёмкостью, можно описать
с помощью активного сопротивления
(отрицательного по величине, т.к. энергия
вносится в колебательный контур, а не
расходуется) и тогда эквивалентная
схема параметрического колебательного
контура (рис.2.1) примет вид (рис.2.18).
Всё,
что стоит в скобках в выражении (2.73)
можно обозначить через вносимое
сопротивление. Поэтому энергию, вносимую
параметрической ёмкостью, можно описать
с помощью активного сопротивления
(отрицательного по величине, т.к. энергия
вносится в колебательный контур, а не
расходуется) и тогда эквивалентная
схема параметрического колебательного
контура (рис.2.1) примет вид (рис.2.18).

Рис.2.18. Эквивалентная схема одноконтурного параметрического усилителя
Мы
получили колебательный контур с
постоянными элементами, для которого
можем записать, что
![]() ;
причем
;
причем![]() мы определили из энергетического
баланса, сравнив мощности: вносимую в
колебательный контур параметрической
емкостью и мощность, расходуемую активным
постоянным сопротивлением. Тогда
получаем:
мы определили из энергетического
баланса, сравнив мощности: вносимую в
колебательный контур параметрической
емкостью и мощность, расходуемую активным
постоянным сопротивлением. Тогда
получаем:
 .
(2.74)
.
(2.74)
Величина
![]() - добротность контура, до момента времени,
когда емкость С(t)
стала параметрической, т.е. при
- добротность контура, до момента времени,
когда емкость С(t)
стала параметрической, т.е. при
![]() .
.
Для
наивыгоднейших фазовых соотношений
между сигналом и накачкой, когда
![]() =0
получаем максимальное значение для
коэффициента передачи
=0
получаем максимальное значение для
коэффициента передачи
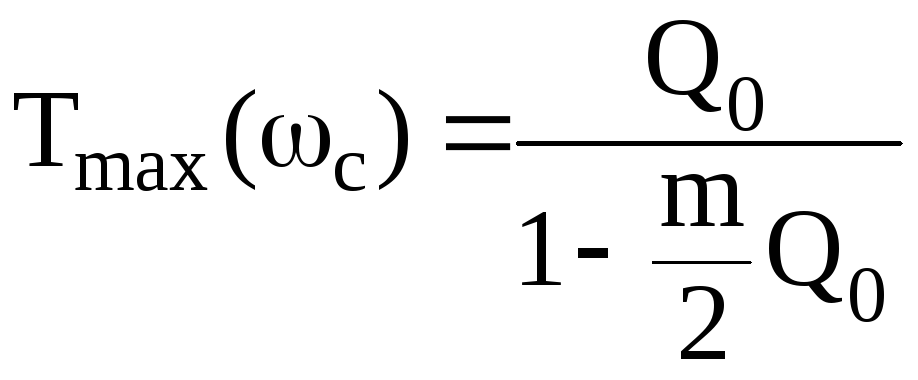 .
(2.75)
.
(2.75)
Следовательно,
из условия
![]() ,
находим, что
,
находим, что
![]() .
.
Таким
образом, можно сделать следующий вывод:
на основном периоде колебаний фаза
может принимать два значения
![]() для которых получается лучшая фазировка.
для которых получается лучшая фазировка.
Если
![]() ,
коэффициент передачи
,
коэффициент передачи![]() принимает конечное значение. Следовательно,
энергия, вносимая в одноконтурный
параметрический усилитель, не превышает
потери и цепь устойчива (т.е. самовозбуждение
колебаний в параметрическом усилителе
невозможно–
такой усилитель называется усилителем
регенеративного типа). Если же
принимает конечное значение. Следовательно,
энергия, вносимая в одноконтурный
параметрический усилитель, не превышает
потери и цепь устойчива (т.е. самовозбуждение
колебаний в параметрическом усилителе
невозможно–
такой усилитель называется усилителем
регенеративного типа). Если же
![]() ,
то
,
то![]() ,
и это говорит о том, что система стала
неустойчивой. В таком усилителе возможно
самовозбуждение колебаний и он
превращается в автогенератор гармонических
колебаний. Граница между устойчивыми
и неустойчивыми колебаниями в
параметрическом усилителе соответствует
случаю, когда вносимая в колебательный
контур энергия в точности равняется
потерям. Поэтому, из равенства
,
и это говорит о том, что система стала
неустойчивой. В таком усилителе возможно
самовозбуждение колебаний и он
превращается в автогенератор гармонических
колебаний. Граница между устойчивыми
и неустойчивыми колебаниями в
параметрическом усилителе соответствует
случаю, когда вносимая в колебательный
контур энергия в точности равняется
потерям. Поэтому, из равенства![]() находим, что
находим, что
![]() ,
(2.76)
,
(2.76)
где
![]() -
затухание колебательного контура (
-
затухание колебательного контура (![]() ).
).
Ранее, когда мы рассматривали изменение ёмкости скачком и выполнялись условия оптимальной накачки, значение для критического коэффициента модуляции принимало значение:
![]() .
.
В нашем случае, при гармоническом изменении емкости, величина для mкр=2d, т.е. больше чем в случае модуляции емкости скачком. Поэтому модуляция емкости скачком, при всех прочих равных условиях, является оптимальной. В этом случае для достижения стационарной амплитуды колебаний в параметрическом усилителе необходимо будет вносить наименьшую порцию энергии с помощью параметрической емкости.
Параметрическое усиление в системе достигается оптимальным образом при правильной фазировке входного сигнала и генератора накачки. Если фазировка не была произведена, то в такой системе можно наблюдать не только отсутствие усиления, но и ослабление входного сигнала. Необходимость жёсткой фазировки сигнала и генератора накачки является основным недостатком одноконтурного параметрического усилителя.
На
рис. 2.19 представлены изменения
параметрической емкости и двух возможных
вариантов колебаний напряжения, которые
могут возникнуть в одноконтурном
параметрическом усилителе. При такой
разности фаз между колебаниями напряжения
U(t)
и колебаниями параметрической емкости
C(t)
(или другими словами, колебаниями
генератора накачки) обеспечивается
минимальное значение коэффициента
модуляции
![]() .
.
Асинхронный режим. Асинхронный режим – это наиболее часто встречающийся на практике режим, т.к. выполнить строгое равенство между частотами двух различных устройств задача большой сложности. Для устранения этого недостатка (требования жесткой синхронизации двух частот) иногда прибегают к параметрическому усилению расстроенным контуром. Рассмотрим работу такого устройства.
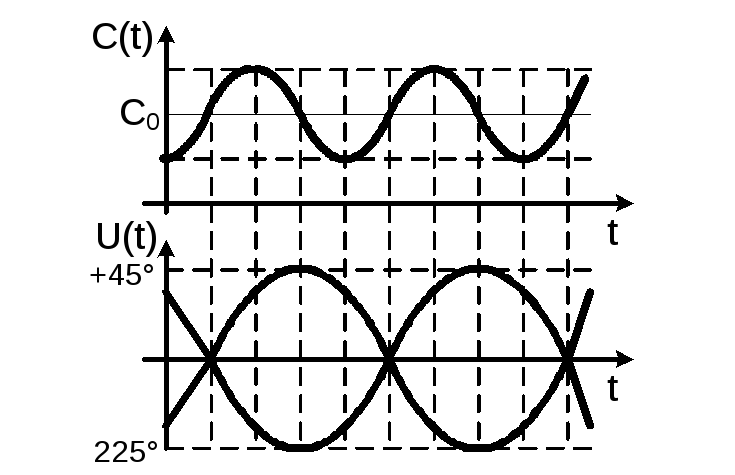
Рис.2.19. Законы изменения C(t) и U(t) в параметрическом контуре
Пусть выполняется следующее соотношение
![]() ,
тогда
,
тогда
![]() .
.
Тогда, с учетом соотношения (2.74) (т.к. считаем что η « 1), получаем
 .
(2.77)
.
(2.77)
В этом случае возникает параметрическая модуляция коэффициента передачи, а значит и выходного колебания связанного с входным следующим соотношением Uвых(t)=T(t)Uвх(t). От паразитной модуляции Uвых(t) частотой η можно избавиться с помощью различных схемных решений, но при этом
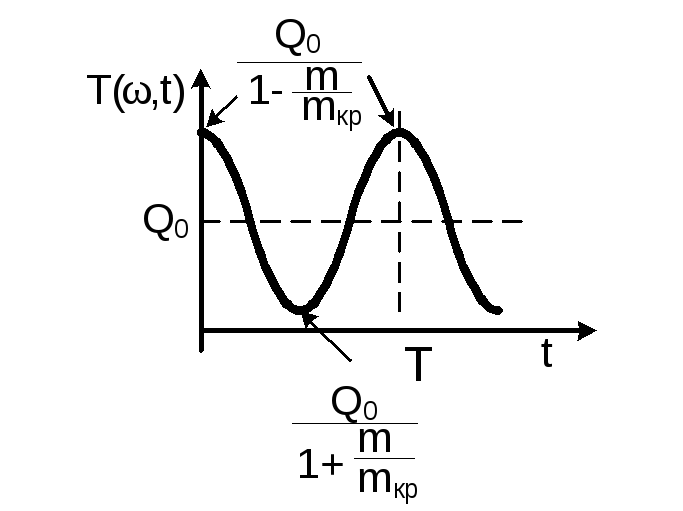
Рис.2.20.
Закон изменения
![]() для асинхронного режима
для асинхронного режима
получить
выигрыш в коэффициенте усиления см.
рис.2.20., т.к. η « 1, а T=![]() –
паразитная модуляция имеет очень большой
период колебаний.
–
паразитная модуляция имеет очень большой
период колебаний.
