§3.7. Метод гармонической линеаризации (мгл)

Метод МГЛ применим для исследования как свободных, так и вынужденных колебаний в нелинейных цепях (системах) (рис.3.45).

Идея метода: если за счет фильтрующих свойств нелинейной системы, колебания в ней близки к гармоническим, то нелинейные элементы в такой

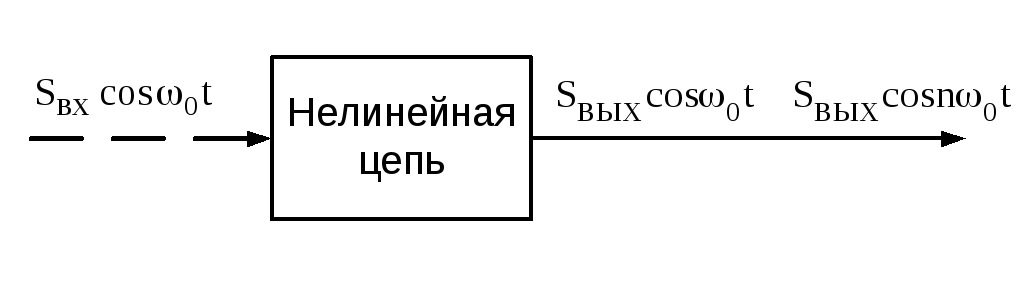
Рис.3.45. Нелинейная цепь

системе можно заменить эквивалентными линейными элементами с параметрами, соответствующими данному режиму гармонических колебаний. Метод применим для исследования стационарных процессов близких к гармоническим в нелинейных системах с ярко выраженными резонансными свойствами. После замены нелинейных элементов линейными, колебания в цепи могут исследоваться любым из методов линейной теории.

§3.7.1. Эквивалентные параметры нелинейных элементов

Рассмотрим нелинейный элемент – нелинейное сопротивление (рис.3.46). Ток задан ВАХ нелинейного элемента. Пусть напряжение, приложенное к обоим

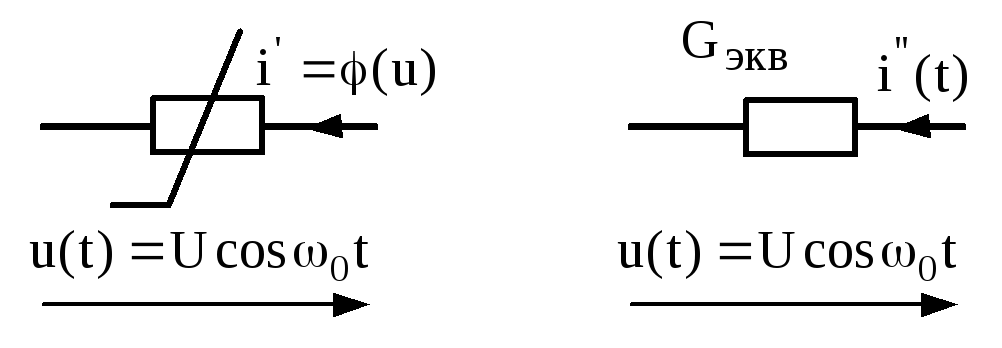
Рис.3.46. Нелинейный элемент проводимость и эквивалентное

ему линейная проводимость

элементам, является гармоническим (в силу резонансных свойств внешней к нелинейному сопротивлению цепи)

= φ (Ucosω ₀t) = cosnω₀t, = G_эквUcosω₀t, (3.44)

где 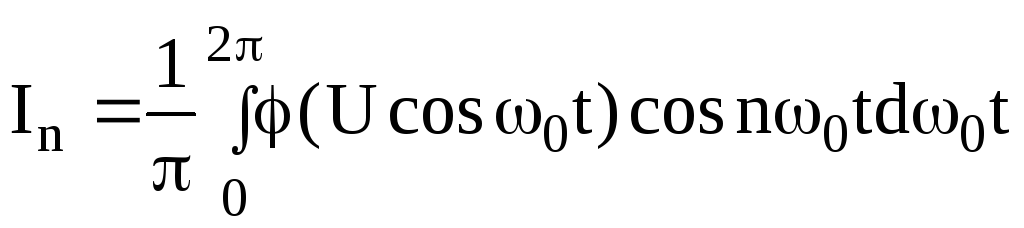. (3.45)

Если нелинейная система включает в себя резонансный контур, то за счет резонансных свойств контура из всех гармоник существенной будет, лишь составляющая основной частоты ω₀. Следовательно, ток i в нелинейном контуре есть

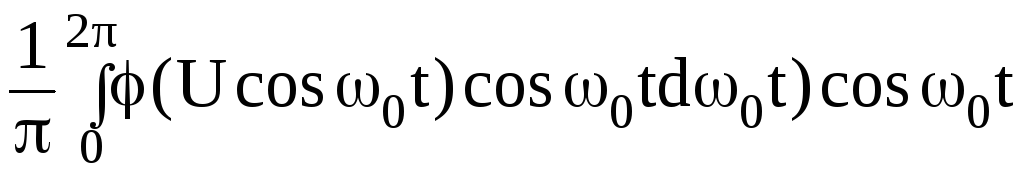= (. (3.46)

Сравнивая токи в нелинейном и эквивалентном ему линейном контурах, получаем, что

G_экв = 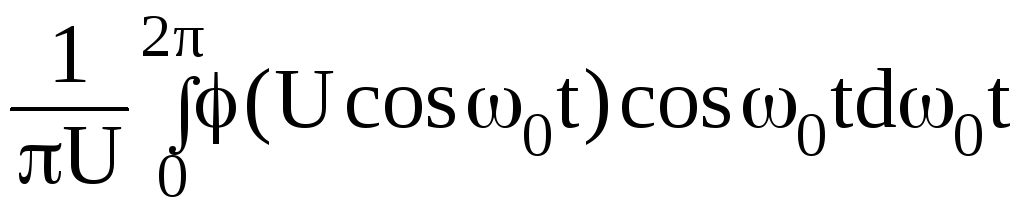. (3.47)

Аналогичным образом можно найти параметры С_экв, L_экв, R_экв:

R_экв = 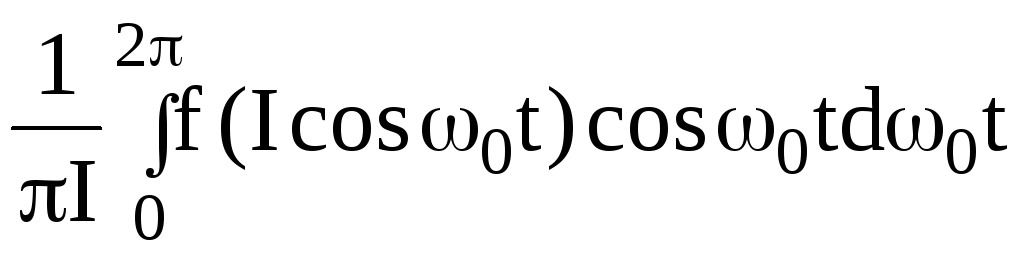; (3.48)

C_экв = 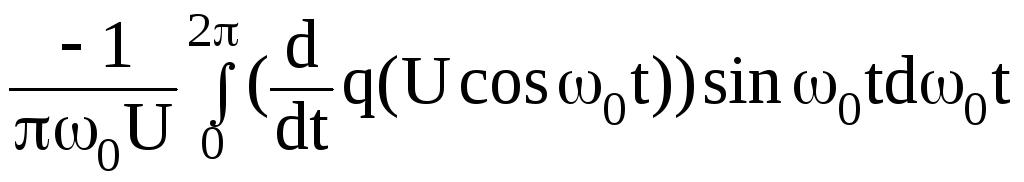; (3.49)

L_экв = . (3.50)

В выражения (3.47 – 3.50), для эквивалентных параметров, входят ВАХ нелинейных элементов. Определим эквивалентные параметры в двух случаях: полиномиальной и кусочно-линейной аппроксимаций.

В случае полиномиальной аппроксимации − ВАХ нелинейных элементов могут быть представлены в виде

φ (U) = a₀ + a₁U + a₂U² + a₃U³ + … (3.51)

Так как закон изменения напряжения у нас гармонический, то u(t)=Ucosω₀t и, следовательно,

φ (Ucosω ₀t) = a₀ + a₁Ucosω ₀t + a₂U²cos²ω ₀t + a₃U³cos³ω ₀t + … = (a₀ + a₂ + …) + (a₁U + . . .) + (a₃U³ + a₅U⁵ + …)cosω ₀t + ( a₂U² + … )cos2ω ₀t + …

Подставляя найденное выражение для ВАХ в выражение для G_экв, получим

G_экв = a₁ + a₃U² + a₅U⁴ + … (3.52)

Аналогично находим эквивалентные параметры нелинейных элементов в случае ампер-веберной и вольт-кулоновской характеристик. Выражение для любого эквивалентного элемента имеет вид

П_экв = a₁ + a₃A² + a₅A⁴ + … , (3.53)

где А – это амплитуда напряжения U для G_экв, C_экв и амплитуда тока I для R_экв , L_экв соответственно.

При кусочно-линейной аппроксимации вида (рис.3.47) ток, протекающий

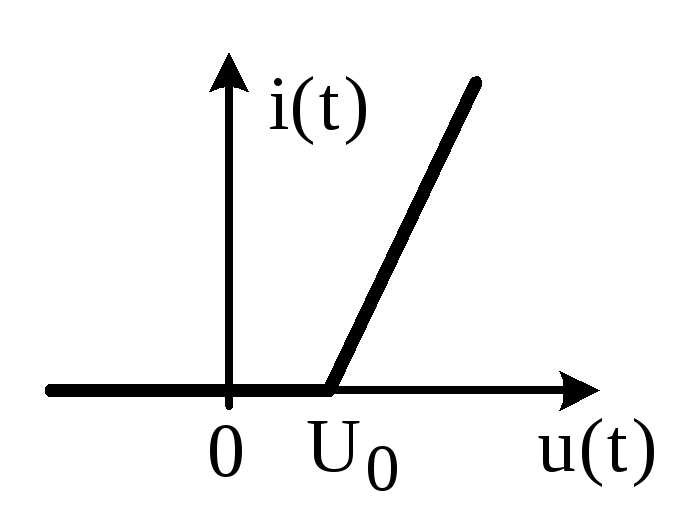
Рис.3.47. Кусочно-линейная аппроксимация нелинейного элемента

через нелинейный элемент равен

i(t) = 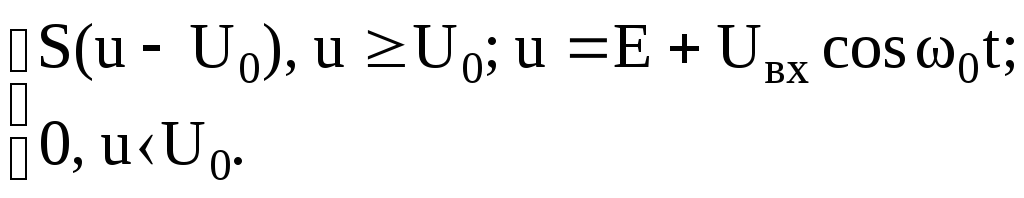(3.54)

С учетом того, что угол отсечки определяется выражением cosθ = , находим

i(t) = 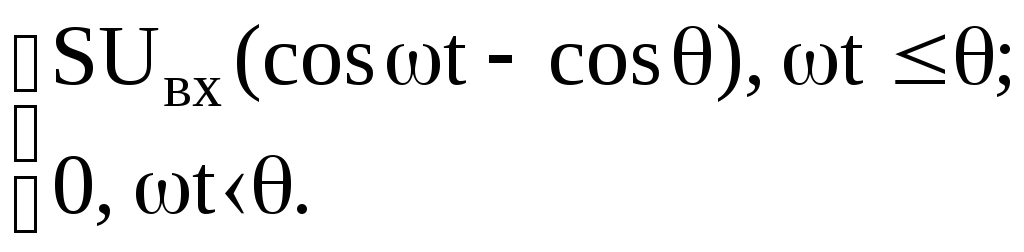(3.55)

Тогда с учетом того, что приложенное напряжение к нелинейному элементу есть гармоническая функция, раскладываем ток в ряд Фурье

i(t) = , где I_n = SU_вх γ(θ), (3.56)

причем γ(θ) = 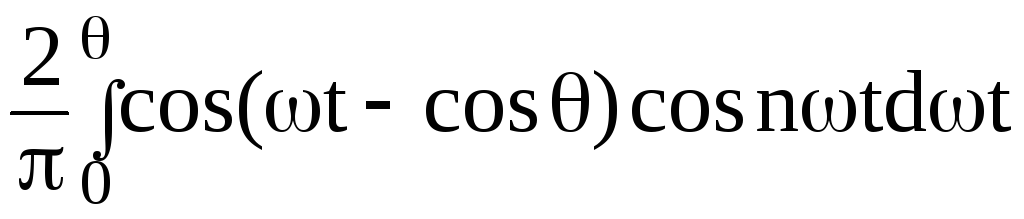(3.57)

- гамма функция, а θ = arccos 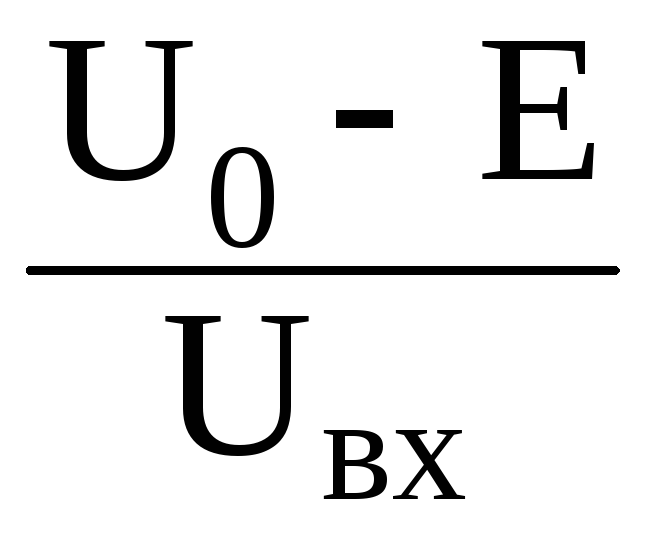. ПоэтомуG_экв=Sγ₁(θ).