- •Министерство образования и науки украины
- •Введение
- •Глава і Свободные и вынужденные колебания в линейных инвариантных динамических системах
- •§1.1.Преобразование Лапласа и его основные свойства
- •§ 1.2. Применение операторного метода для анализа процессов в цепях с сосредоточенными элементами
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях
- •§1.4 Общий вид решения задачи анализа прохождения сигнала через устойчивую линейную цепь
- •Алгоритм решения задач анализа вынужденных колебаний в электрических цепях
- •§1.5. Свободные колебания в динамических системах с распределенными элементами
- •§1.5.1. Классификация длинных линий
- •§1.5.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •Глава іі Колебания в линейных параметрических системах Линейные параметрические цепи
- •§ 2.1. Изменение спектра входного сигнала при прохождении через линейные параметрические цепи
- •§ 2.2. Аксиоматика теории цепей в параметрическом случае
- •§2.3. Прохождение сигналов через параметрические r – цепи
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с одной степенью свободы. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.5.1. Процессы в механической параметрической колебательной
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.6. Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье
- •§ 2.7. Параметрическое усиление колебаний в одноконтурной системе. Синхронный режим. Асинхронный режим
- •§2.8. Параметрический генератор (параметрон)
- •§2.9. Двухконтурные параметрические системы
- •§2.9.1.Теорема Менли-Роу
- •§2.9.2 .Двухконтурный параметрический усилитель нерегененративного типа
- •§2.9.3 .Двухконтурный параметрический усилитель регененративного типа
- •§ 2.9.4 Параметрические умножение и деление частоты
- •§2.11. Некоторые приближенные методы исследования процессов в параметрических системах
- •§2.11.1. Метод «замороженного» параметра
- •§2.11.2. Алгоритм метода замороженного параметра для задачи о свободных и вынужденных колебаниях в параметрических цепях
- •§2.11.3 Метод последовательных приближений
- •§2.11.3. Метод вкб (Вентцеля-Крамера-Бриллюэна)
- •Глава ш Анализ колебаний в нелинейных цепях
- •§3.1. Нелинейные элементы цепей
- •§3.2 Аппроксимация характеристик нелинейных элементов
- •§3.3 Преобразование спектра колебаний нелинейной цепью
- •§3.4 Особенности задач анализа колебаний в нелинейных цепях
- •§3.5 Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений
- •§3.6. Метод линеаризации
- •§3.7. Метод гармонической линеаризации (мгл)
- •§3.7.1. Эквивалентные параметры нелинейных элементов
- •§3.7.2. Автогенератор гармонических колебаний.
- •§3.8. Методы малого параметра. Метод последовательных приближений
- •§3.9. Метод медленно меняющихся амплитуд (ммма).
- •§3.10. Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде
- •§3.11. Метод фазовой плоскости
- •§3.11. 1.Метод фазовой плоскости. Метод изоклин
- •§3.11.2. Метод фазовой плоскости. Особые точки
- •§3.11.2.Исследование методом фазовой плоскости схемы на
- •§1.1. Преобразование Лапласа и его основные свойства 7
- •610077,М. Харків, пл. Свободи, 4.
- •610077,М. Харків, пл. Свободи, 4.
§ 2.2. Аксиоматика теории цепей в параметрическом случае
Первичными понятиями, как и для линейных цепей, являются напряжение U и ток i. Элементы, источник напряжения и источник тока, законы Киргофа – являются универсальными. Отличие в элементах R, L и С.

 U=Ri;
i=GU; U(t)=R(t)i(t); i(t)=G(t)U(t)
P=Ui=Ri2=GU2>0
P(t)=R(t)i2(t)=G(t)U2(t)>0
(2.5)
U=Ri;
i=GU; U(t)=R(t)i(t); i(t)=G(t)U(t)
P=Ui=Ri2=GU2>0
P(t)=R(t)i2(t)=G(t)U2(t)>0
(2.5)




![]() ;
;
![]() ;
(2.6)
;
(2.6)
 ;
;
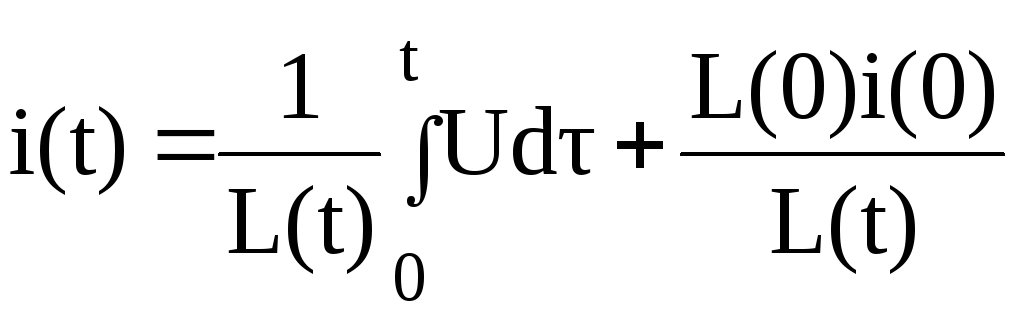 ;
(2.7)
;
(2.7)

![]() PL=L
PL=L![]() 0;
0;
![]() .
(2.8)
.
(2.8)
Слагаемое
![]() в выражении (2.6) подобно падению напряжения
на сопротивлении. Причем, если
в выражении (2.6) подобно падению напряжения
на сопротивлении. Причем, если![]() >0,
то можно отбирать энергию с помощьюL(t)
из цепи, а если
>0,
то можно отбирать энергию с помощьюL(t)
из цепи, а если
![]() <0,
то это описывает случай внесения энергии
в цепь с помощью параметрического
элемента. Аналогично и для мощностиPL,
наличие
<0,
то это описывает случай внесения энергии
в цепь с помощью параметрического
элемента. Аналогично и для мощностиPL,
наличие


слагаемого
![]() свидетельствует о возможности вносить
или отбирать энергию из цепи, в
зависимости от знака
свидетельствует о возможности вносить
или отбирать энергию из цепи, в
зависимости от знака![]() .
.
![]() ;
;
![]() ;
(2.9)
;
(2.9)
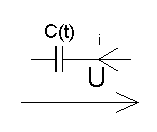
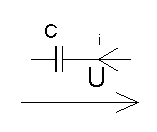
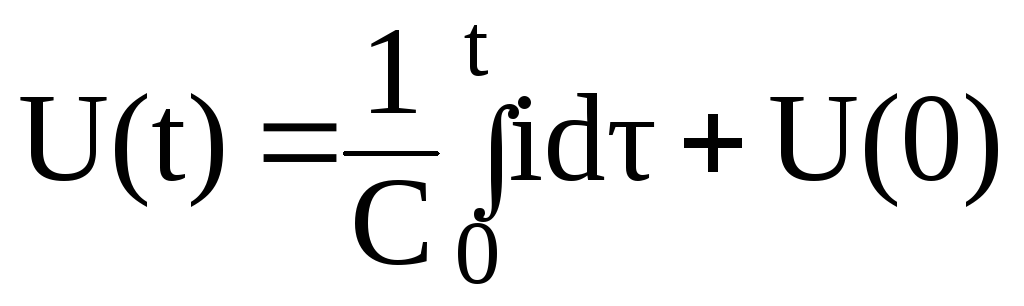 ;
;
 ;
(2.10)
;
(2.10)

![]() PС=C
PС=C![]() 0;
0;
![]() .
(2.11)
.
(2.11)
Слагаемое
![]() в выражении (2.9) подобно току, протекающему
через проводимость. Причем если
в выражении (2.9) подобно току, протекающему
через проводимость. Причем если![]() >0, то можно отбирать энергию с помощью
переменной емкости С(t)
из цепи, а если
>0, то можно отбирать энергию с помощью
переменной емкости С(t)
из цепи, а если
![]() <0,
то это описывает случай внесения энергии
в цепь с помощью параметрического
элемента. Аналогично и для мощностиPC,
наличие
слагаемого
<0,
то это описывает случай внесения энергии
в цепь с помощью параметрического
элемента. Аналогично и для мощностиPC,
наличие
слагаемого
![]() свидетельствует о возможности вносить
или отбирать энергию из цепи, в зависимости
от знака
свидетельствует о возможности вносить
или отбирать энергию из цепи, в зависимости
от знака![]() .
.
При уменьшении емкости в цепь вносится энергия, при увеличении емкости энергия забирается из цепи.
Таким образом, реактивные параметрические элементы L(t) и C(t) выступают в роли преобразователей энергии, т.е. параметрическое возбуждение и усиление колебаний происходит в результате периодического изменения энергоемких параметров колебательной системы, определяющих ее частоту.
В рассмотренных ранее генераторах и усилителях (схемах в которых пренебрегали нелинейными свойствами элементов, т.е. считали, что цепи составлены из линейных элементов) возбуждение и усиление колебаний осуществлялось за счет энергии источников постоянного напряжения. С энергетической точки зрения такие усилители и генераторы являются преобразователями энергии постоянного напряжения (тока) в энергию переменного напряжения (тока).
В параметрических генераторах и усилителях механизм передачи энергии (или накачки) оказывается иным: энергия вводится в систему путем изменения с некоторый частотой реактивного параметра, на что какой-то источник затрачивает энергию. Поскольку параметр меняется с одной частотой, а возбужденные или усиленные колебания в большинстве случаев имеют другую частоту, рассматриваемые параметрические устройства оказываются преобразователями частоты.
Давайте вспомним, что уравнения, описывающие колебания в радиотехнических цепях, составляются с помощью хорошо известных методов МКТ и МУН, причем для параметрических систем они имеют вид приведенный в таблице 2.
Уравнения, приведенные в Таблице 2, должны быть дополнены соответствующими начальными условиями (задача Коши).
Таблица 2
|
МКТ
|
|
|
Неоднородная система линейных интегродифференциаль-ных уравнений с переменными коэффициентами | ||
|
МУН |
|
|
Неоднородная система линейных интегродифференциаль-ных уравнений с переменными коэффициентами
| ||
Уравнения длинных линий с переменными параметрами имеют вид:
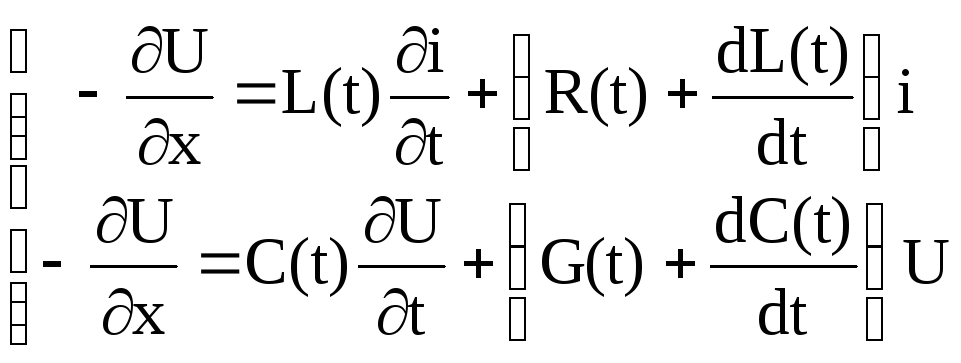 (2.12)
(2.12)
и дополняются соответствующими начальным и граничным условиями.
Необходимо отметить, что колебания в параметрических устройствах описываются параметрическими уравнениями общего метода решения которых нет. Т.е. для линейных параметрических цепей нельзя в общем случае построить решение задачи анализа колебательного процесса.
Решение построено только для частных случаев:
1.
Если цепь состоит только из сопротивлений
R,
тогда уравнение, описывающее колебания
в такой системе, имеет вид:
![]() - система алгебраических уравнений.
- система алгебраических уравнений.
2. Если в резистивной цепи имеется один энергоемкий элемент, тогда процесс описывается дифференциальным уравнением первого порядка (уравнение с полуцелой степенью свободы) (2.13). Для таких систем разработан метод называемый методом Туркина.
![]() (2.13)
(2.13)
3. Если колебательный процесс описывается дифференциальным уравнением второго порядка (2.14)
![]() (2.14)
(2.14)
то его можно свести к какому-нибудь известному уравнению с переменными коэффициентами (например, к уравнению Матье, Хилла, Бесселя и др.).
4. Если параметры элементов цепи изменяются значительно медленнее колебаний u(t) и i(t), тогда применимы приближенные методы.
Выводы. С помощью переменных индуктивностей и емкостей можно изменять энергию системы, поэтому характер свободных колебаний в параметрических системах может существенно отличаться от колебаний в системах с постоянными элементами.
Следует также отметить, что для линейных параметрических систем применим принцип наложения, следовательно, в задачах прохождения сигналов через устойчивые параметрические цепи решение может быть представлено в интегральном виде:
![]() ,
(2.15)
,
(2.15)
либо
 ,
(2.16)
,
(2.16)
либо
![]() ,
(2.17)
,
(2.17)
где
![]() –
параметрические функции цепей, отыскание
которых также встречает принципиальные
трудности. Именно поэтому ключевыми
задачами в теории параметрических
систем являются задачи по определению
отклика на гармоническое или импульсное
воздействия.
–
параметрические функции цепей, отыскание
которых также встречает принципиальные
трудности. Именно поэтому ключевыми
задачами в теории параметрических
систем являются задачи по определению
отклика на гармоническое или импульсное
воздействия.
Одним
из важнейших свойств, принципиально
отличающих параметрические цепи от
линейных, является следующее: в
параметрических системах с переменными
параметрами происходит обогащение
спектра колебаний – возникают новые
гармонические составляющие комбинационных
частот. Например, в R
– цепи с периодическим коэффициентом
передачи
![]() ,
возбуждаемой периодическим сигналом
,
возбуждаемой периодическим сигналом![]() ,
выходное колебание
,
выходное колебание
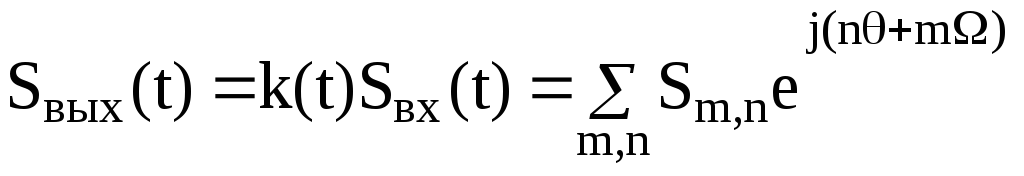 (2.18)
(2.18)
содержит
гармонические составляющие комбинационных
частот
![]() .
.