Глава і Свободные и вынужденные колебания в линейных инвариантных динамических системах

§1.1.Преобразование Лапласа и его основные свойства

В технических науках, в особенности в теории линейных электрических цепей, технической кибернетике и т. д. широко используется преобразование Лапласа. Это интегральное преобразование, которое определенным функциям f(t) действительного переменного t, называемыми оригиналами, по формуле

F(p)= (1.1)

ставит в соответствие функции F(p) комплексного переменного p=δ+iω, называемых изображениями. Для связи f(t) и F(p) вместо (1.1) используют различные обозначения, в том числе F(p)=[f(t)] или f(t) F(p), где - оператор прямого преобразования Лапласа.

Обычно к классу функций – оригиналов относят «классические» функции ограниченного роста, удовлетворяющие условиям Дирихле и отличные от нуля при t≥0. Для ряда важных приложений удобно класс оригиналов расширить, включив в него обобщенные функции – импульсную функцию Дирака δ(t) и ее производные. Правомерность такого расширения обоснована в теории обобщенных функций.

Найдем изображения некоторых важных для практики функций:

а) Изображение единичной ступенчатой функции

σ(t)═, [σ(t)]== (1.2)

б) Изображение экспоненциальной функции

f(t)= = e F(p)= = (1.3)

в) Изображение импульсной функции Дирака

F(p)=[δ(t)]== e^-p0 = 1 (1.4)

Приведенные ниже свойства преобразования Лапласа являются основными для его широкой применимости. Они соответствуют операциям, которые выполняются над функциями-оригиналами, причем каждый раз функция, являющаяся результатом той или иной операции, должна принадлежать к классу функций – оригиналов. Во всех свойствах F(p) – это изображение исходной функции – оригинала, подвергаемой различным операциям:

1. Линейность преобразования:

[] = (1.5)

2. Изображение производной:

[] =pⁿ (1.6)

3. Изображение интеграла:

[]= (1.7)

4. Изображение функции с запаздывающим аргументом:

[f(t-θ)] = e^-p F(p) (1.8)

5. Изображение свертки функций:

[dτ]=F₁(p)F₂(p) (1.9)

6. Изображение функции с экспоненциальным сомножителем:

[f(t)e^at]=F(p-a) (1.10)

7. Изображение функции с измененным масштабом:

[f(аt)]=F() (1.11)

8. Изображение функции с сомножителем tⁿ:

[tⁿ f(t)]=(-1)ⁿ F⁽ⁿ⁾(p) (1.12)

8. Изображение функции с сомножителем :

[f(t)]= (1.13)

8. Изображение произведения функций:

[f₁(t) f(t)]=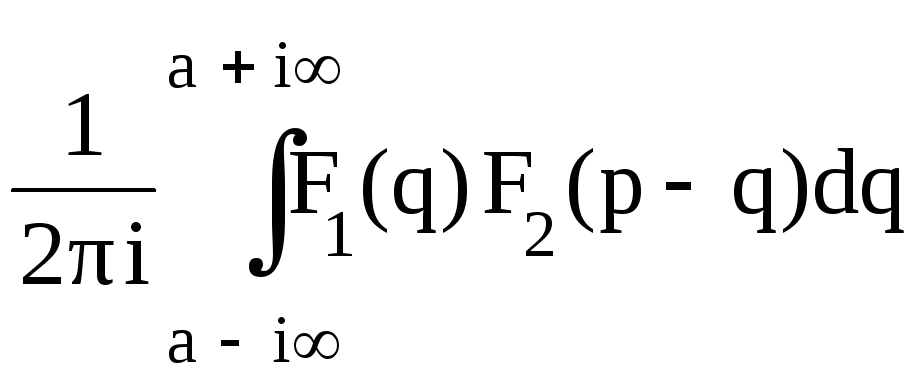 (1.14)

Зачастую изображения можно находить без сложного вычисления интеграла Лапласа, лишь путем использования перечисленных свойств.

Пример: а) Найти изображение косинусоидальной функции:

Acosω₀tσ(t)=½ A(e^iωt + e^-iωt) σ(t)½ A()=(1.15)

б) Найти изображение прямоугольного импульса:

П(t)=A[σ(t) - σ(t-θ)] (1 - e^{-p θ}) (1.16)

в) Найти изображение косинусоидальной функции с изменяющейся амплитудой:

A(t) cosωt σ(t) =½A(t) (e^iωt + e^-iωt) σ(t)½[A(p-iω) + A(p+iω)]. (1.17)

Обратное преобразование Лапласа, однозначно восстанавливающее оригинал по своему изображению, определяется интегралом:

f(t)= [F(p)]=. (1.18)

Особую значимость для приложений имеет обратное преобразование дробно-рациональных функций F(p)=. Такую функцию достаточно разложить на элементарные дроби и, воспользовавшись свойством линейности, ограничиться преобразованием дробей (для случая, когда все корни простые)

F(p)=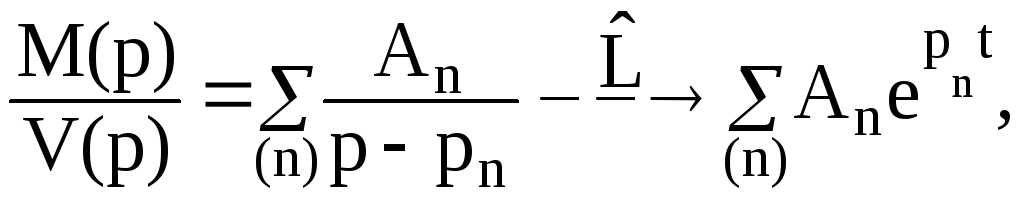(t≥0). (1.19)