§3.9. Метод медленно меняющихся амплитуд (ммма).

Вывод укороченных уравнений

МММА применяется для анализа нелинейных уравнений, достаточно близких к линейным уравнениям. Достаточно близкими к линейным, обычно называются колебания, для которых соответствующие дифференциальные уравнения хотя и являются нелинейными, но содержат некоторый параметр ε, входящий в эти уравнения так, что при нулевом значении ε они вырождаются в линейные дифференциальные уравнения с постоянными коэффициентами. При этом предполагается, что параметр ε является «малым».

Представим себе, что система настолько близка к линейной, что колебания в течение одного периода имеют форму, весьма близкую к гармонической. Если рассматривать колебания на большом интервале времени (по сравнению с периодом колебания), то уже существенно будет проявляться влияние даже малых отклонений системы от линейной, выражающееся в наличии малых нелинейных слагаемых в дифференциальных уравнениях. Таким образом, малые нелинейные члены могут оказывать как бы коммулятивное действие.

Совершенно естественно, что наиболее доступными для исследования являются колебания системы с малой нелинейностью, поскольку к ним в той или иной форме можно применять метод возмущений.

Исследование систем с большой нелинейностью является с математической точки зрения весьма трудной проблемой, требующей индивидуального подхода в каждом конкретном случае.

В настоящее время существует целый ряд методов позволяющих исследовать системы с одной степенью свободы при малых нелинейностях. В общем виде такие системы описываются дифференциальными уравнениями следующего вида:

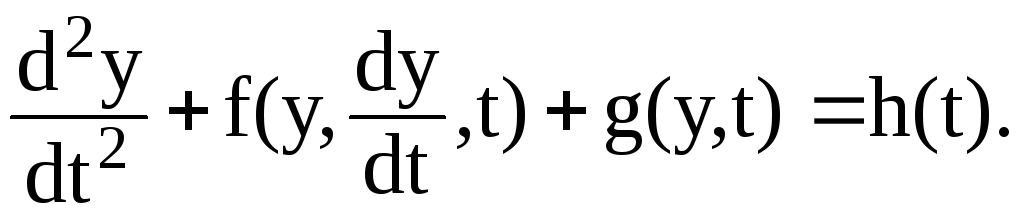(3.77)

Если удается выделить малый параметр, то уравнение преобразовывается к виду:

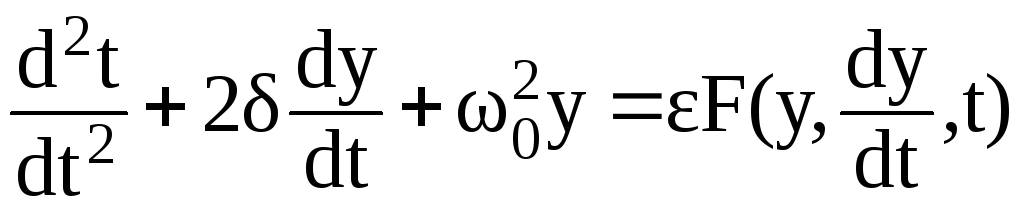. (3.78)

В теории колебаний используется ряд методов, основанных на малом параметре при нелинейной части дифференциальных уравнений 2^го и более высоких порядков. Это метод возмущений Пуанкаре, метод медленно меняющихся амплитуд Ван-дер-Поля, метод амплитудной плоскости (метод Андронова-Витта), метод Боголюбова-Крылова, асимптотический метод Боголюбова-Митропольского и другие.

Рассмотрим один из них – МММА. Данный метод так же, как и МГЛ, применим в тех случаях, когда возникающее колебание близко по форме к гармоническому, что обычно имеет место при использовании в автогенераторах контура с достаточно высокой избирательностью.

Уравнение, описывающее процессы в таких системах, может быть записано в виде:

, (3.79)

или в безразмерных переменных оно имеет вид:

.

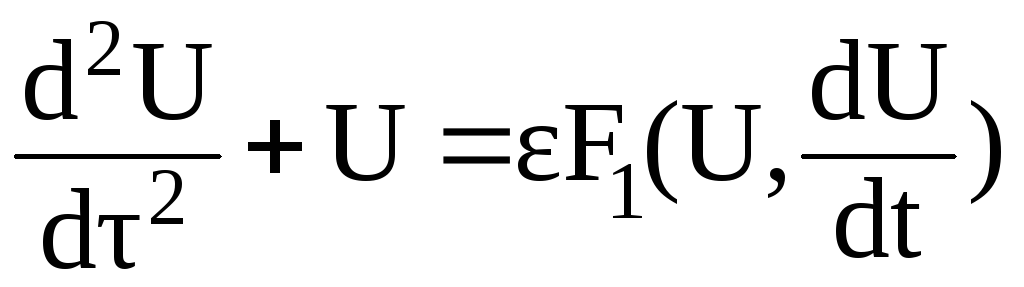Переходя от анализа одного дифференциального уравнения относительно одной переменной U к анализу системы двух уравнений относительно двух переменных U и V:

(3.80)

Если параметр ε равен 0, то решение уравнения (3.80) имеет вид:

(3.81)

где А и φ – произвольные постоянные.

В методе медленно меняющихся амплитуд решение системы уравнений (3.79) ищем в виде выражений, отличающихся от решения (3.81) тем, что амплитуда А и фаза φ считаются некоторыми функциями времени А(τ) и φ(τ). Тогда

(3.82)

Подставляя системы уравнений (3.81) и (3.82) в уравнение (3.80), получаем:

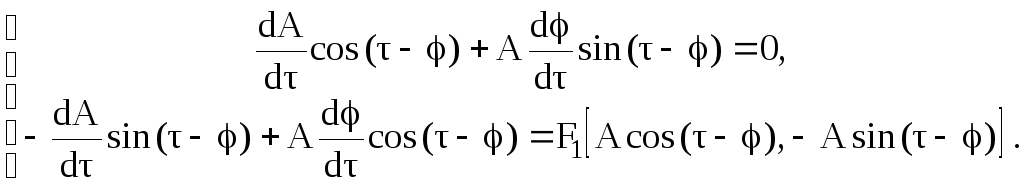
Решение этих уравнений относительно идает:

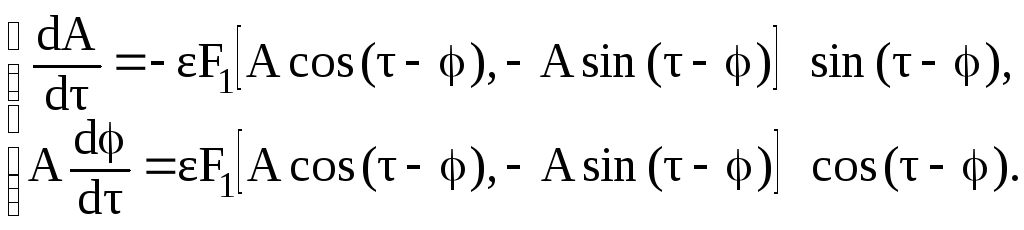(3.83)

Правые части этих уравнений являются функциями времени (α = τ – φ ) с периодом 2π, что позволяет разложить их в ряд Фурье:

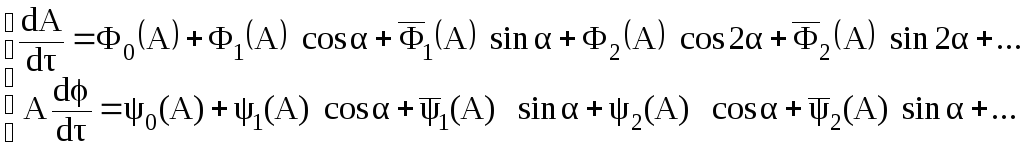(3.84)

Коэффициенты рядов Фурье оказываются функциями амплитуд А. Поскольку до сих пор никаких ограничений на зависимость А(τ) и φ(τ) не накладывалось, уравнения (3.83) являются столь же точными, как и уравнения (3.80) или (3.79). Теперь примем во внимание, что при наличии малого параметра амплитуда А и фаза φ могут изменяться только медленно, т.е. на малую величину за период 2π. Поэтому при этом можно предположить, что в пределах одного периода изменения А и φ происходят с постоянными средними скоростями, соответствующими первым слагаемым рядов Фурье, стоящими в правых частях уравнений (3.84). Результаты такого усреднения правых частей уравнений (3.84) получаем в виде:

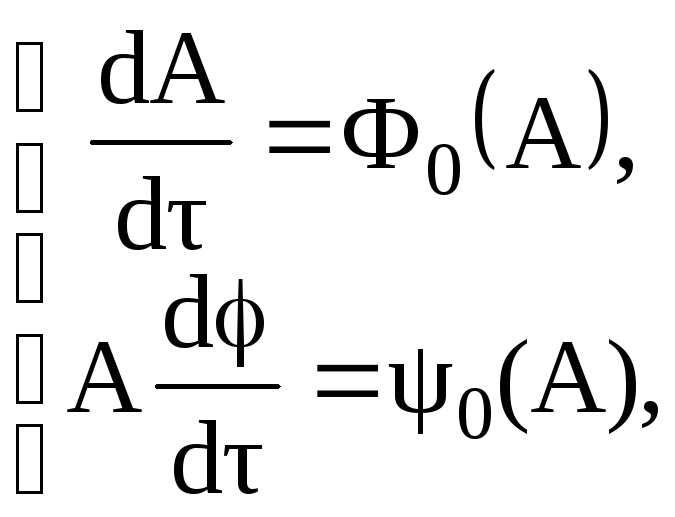(3.85)

где (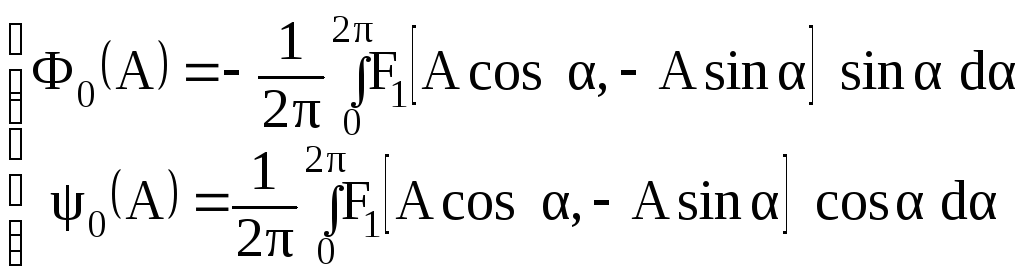3.86)

Уравнения (3.85) называются укороченными, т.к. они получаются в результате отбрасывания ряда слагаемых уравнения (3.84) или уравнениями медленно меняющихся амплитуд и фаз, поскольку они справедливы в тех случаях, когда А и φ медленно (мало) меняются за период колебаний. Из уравнения (3.85) следует, что в процессе установления колебаний, т.е. при изменении амплитуды А, происходит изменение и величины . Следовательно, во время этого процесса мгновенная частота колебаний ω^/, определяемая как

ω^/ =

также меняется.