
- •Министерство образования и науки украины
- •Введение
- •Глава і Свободные и вынужденные колебания в линейных инвариантных динамических системах
- •§1.1.Преобразование Лапласа и его основные свойства
- •§ 1.2. Применение операторного метода для анализа процессов в цепях с сосредоточенными элементами
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях
- •§1.4 Общий вид решения задачи анализа прохождения сигнала через устойчивую линейную цепь
- •Алгоритм решения задач анализа вынужденных колебаний в электрических цепях
- •§1.5. Свободные колебания в динамических системах с распределенными элементами
- •§1.5.1. Классификация длинных линий
- •§1.5.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •Глава іі Колебания в линейных параметрических системах Линейные параметрические цепи
- •§ 2.1. Изменение спектра входного сигнала при прохождении через линейные параметрические цепи
- •§ 2.2. Аксиоматика теории цепей в параметрическом случае
- •§2.3. Прохождение сигналов через параметрические r – цепи
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с одной степенью свободы. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.5.1. Процессы в механической параметрической колебательной
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.6. Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье
- •§ 2.7. Параметрическое усиление колебаний в одноконтурной системе. Синхронный режим. Асинхронный режим
- •§2.8. Параметрический генератор (параметрон)
- •§2.9. Двухконтурные параметрические системы
- •§2.9.1.Теорема Менли-Роу
- •§2.9.2 .Двухконтурный параметрический усилитель нерегененративного типа
- •§2.9.3 .Двухконтурный параметрический усилитель регененративного типа
- •§ 2.9.4 Параметрические умножение и деление частоты
- •§2.11. Некоторые приближенные методы исследования процессов в параметрических системах
- •§2.11.1. Метод «замороженного» параметра
- •§2.11.2. Алгоритм метода замороженного параметра для задачи о свободных и вынужденных колебаниях в параметрических цепях
- •§2.11.3 Метод последовательных приближений
- •§2.11.3. Метод вкб (Вентцеля-Крамера-Бриллюэна)
- •Глава ш Анализ колебаний в нелинейных цепях
- •§3.1. Нелинейные элементы цепей
- •§3.2 Аппроксимация характеристик нелинейных элементов
- •§3.3 Преобразование спектра колебаний нелинейной цепью
- •§3.4 Особенности задач анализа колебаний в нелинейных цепях
- •§3.5 Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений
- •§3.6. Метод линеаризации
- •§3.7. Метод гармонической линеаризации (мгл)
- •§3.7.1. Эквивалентные параметры нелинейных элементов
- •§3.7.2. Автогенератор гармонических колебаний.
- •§3.8. Методы малого параметра. Метод последовательных приближений
- •§3.9. Метод медленно меняющихся амплитуд (ммма).
- •§3.10. Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде
- •§3.11. Метод фазовой плоскости
- •§3.11. 1.Метод фазовой плоскости. Метод изоклин
- •§3.11.2. Метод фазовой плоскости. Особые точки
- •§3.11.2.Исследование методом фазовой плоскости схемы на
- •§1.1. Преобразование Лапласа и его основные свойства 7
- •610077,М. Харків, пл. Свободи, 4.
- •610077,М. Харків, пл. Свободи, 4.
§3.6. Метод линеаризации
Метод основан на предположении, что колебания возбужденные в цепи, содержащей нелинейные элементы, являются настолько малыми, что участки характеристик нелинейных элементов, в пределах которых существуют колебания, могут считаться линейными.
Метод используется:
для анализа малых вынужденных колебаний в устойчивых цепях с нелинейными элементами
для исследования устойчивости цепи при малых отклонениях от состояния покоя
для исследования устойчивости периодического автоколебания.
Метод
линеаризации использовался ранее при
выводе схем замещения электронных
приборов. Причем, параметры электронных
ламп S
=
![]() и
и
 ,
а также параметры транзисторов gвх,
gобр,
gi
и S
– являются дифференциальными параметрами,
определенными для некоторой окрестности
рабочей точки (рекомендованной). Как
следствие этого обстоятельства, анализ
всех схем, содержащих электронные
приборы (усилители разнообразного
назначения), был проведен ранее именно
методом линеаризации.
,
а также параметры транзисторов gвх,
gобр,
gi
и S
– являются дифференциальными параметрами,
определенными для некоторой окрестности
рабочей точки (рекомендованной). Как
следствие этого обстоятельства, анализ
всех схем, содержащих электронные
приборы (усилители разнообразного
назначения), был проведен ранее именно
методом линеаризации.
Рассмотрим применение метода линеаризации для исследования устойчивости цепи при малых отклонениях от состояния покоя.
Пусть некоторая цепь содержит нелинейные устройства, а также генераторы энергии в виде источников постоянного напряжения или тока. Если колебания в цепи отсутствуют, то ее состояние покоя характеризуется постоянными значениями токов I0 и напряжений U0 ветвей, которые могут быть определены анализом режима постоянного тока. Постоянные значения токов и напряжений нелинейных элементов определяют положения рабочих точек на их характеристиках.
При возбуждении каким-либо образом цепи, колебаниями реакции будут отклонения ∆ U и ∆ i токов и напряжений от постоянных значений. Для анализа этих колебаний, от схемы цепи переходим к схеме замещения для режима колебаний, причем нелинейные элементы заменяем линейными с параметрами, равными дифференциальным параметрам в определенной рабочей точке. Составляем систему интегродифференциальных уравнений для отклонений (колебаний). В операторной форме система уравнений имеет вид:
![]() или
или
![]()
(справа в системе уравнений могут быть записаны изображения характеристических источников, вызывающих колебания в цепи).
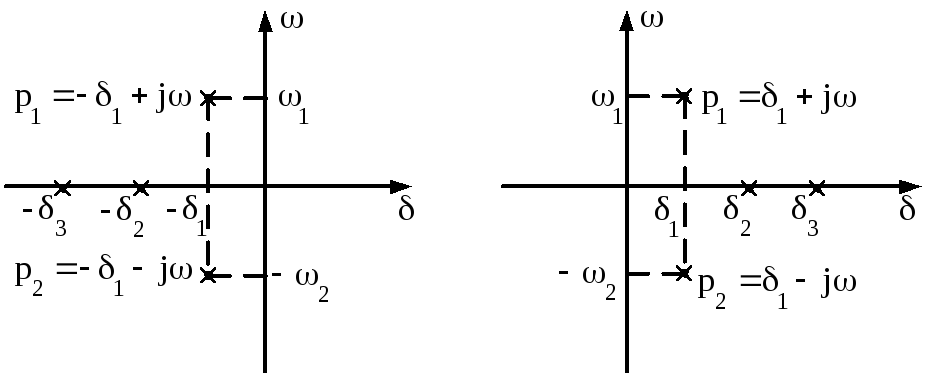
Характер колебаний в цепи определяется расположением корней (рис.3.16) характеристического уравнения
![]()
![]() или
pn+a1pn-1+a2pn-2+…+an=0.
или
pn+a1pn-1+a2pn-2+…+an=0.
Если все корни характеристического уравнения имеют отрицательные вещественные части (т.е. если они лежат в левой полуплоскости) (рис.3.16.а), тогда цепь является устойчивой, а решения принимают вид:
Se![]() и
Sn
и
Sn![]() cos(ωnt+ψn).
cos(ωnt+ψn).
а б
Рис.3.16. Расположение корней характеристического полинома на
плоскости оператора р=δ ± jω: а − для устойчивой цепи, б − для
устойчивой цепи (автогенератора)
С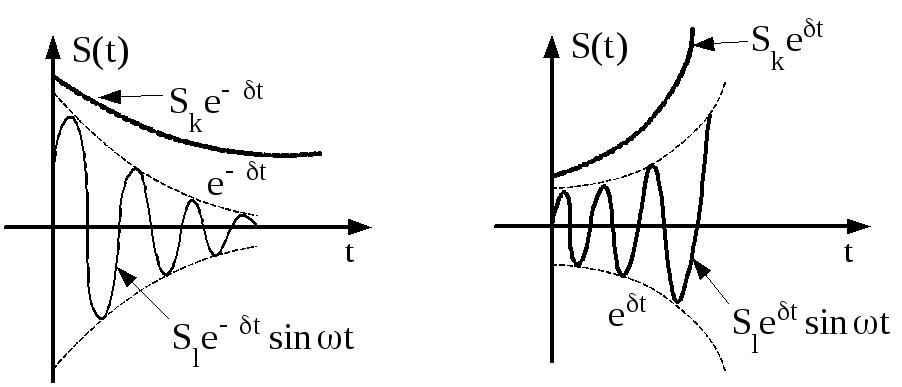 вободные
колебания в этом случае носят затухающий
характер (рис.3.17.а) для гамонических
колебаний и для апериодических колебаний.
вободные
колебания в этом случае носят затухающий
характер (рис.3.17.а) для гамонических
колебаний и для апериодических колебаний.
а) б)
Рис.3.17. Поведение решений для: а − затухающих колебаний,
б − нарастающих колебаний
Если какие-либо из корней характеристического уравнения будет иметь положительную вещественную часть рис.3.16.б, тогда им в решении будут соответствовать слагаемые вида:
Se![]() и
Sn
и
Sn![]() cos(ωnt+ψn).
cos(ωnt+ψn).
Представленные колебания, являются расходящимися (см. рис.3.17.б). Такая цепь является неустойчивой.
Если характеристическое уравнение имеет порядок выше третьего, то корни не имеют аналитических выражений, связывающих их с коэффициентами ak. Для анализа устойчивости следует либо вычислить корни уравнения каким-либо численным методом, либо использовать один из критериев устойчивости, определяющий требования, которым должны удовлетворять коэффициенты ak, для того, чтобы цепи были устойчивы. Наиболее широкое распространение получили критерии Рауса – Гурвица, Михайлова и Найквиста.
Алгоритм метода линеаризации для анализа вынужденных колебаний

Рис.3.18. Алгоритм метода линеаризации для анализа вынужденных
колебаний
Критерий устойчивости Рауса – Гурвица является аналитическим, критерии Михайлова и Найквиста – графоаналитическими. Критерий Рауса-Гурвица предполагает рассмотрение главного определителя вида
Dn
=
 .
.
Из этого определителя, убирая по одному крайнему столбцу и по одной нижней строке, мы получим набор определителей следующего вида:
первый
определитель D1=a1;
второй определитель
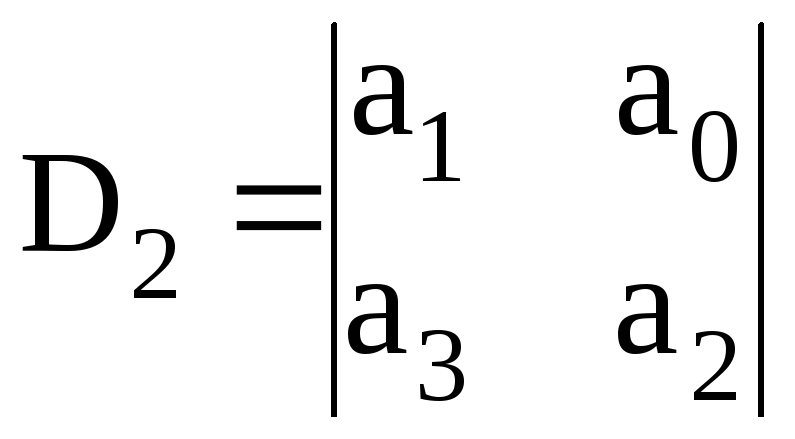 ;
третий определитель
;
третий определитель
D3=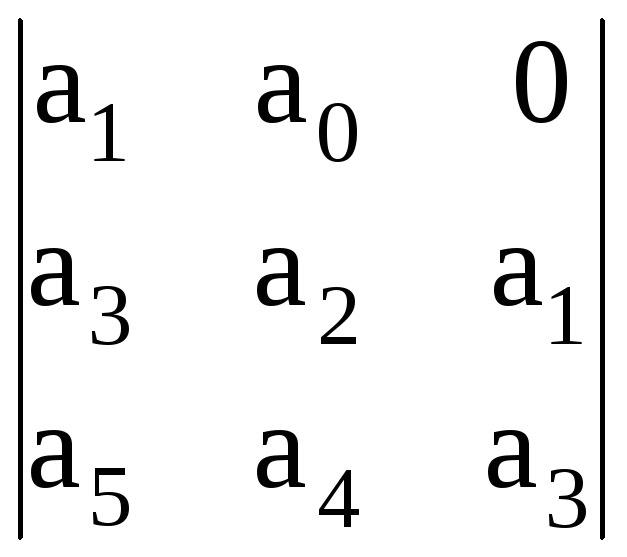 и т.д.
и т.д.
Критерий Рауса – Гурвица устанавливает, что при a0>0 все корни характеристического уравнения имеют положительные вещественные части тогда и только тогда, когда все n определителей положительны.
На рис.3.18 представлен алгоритм исследования колебаний с помощью метода линеаризации.
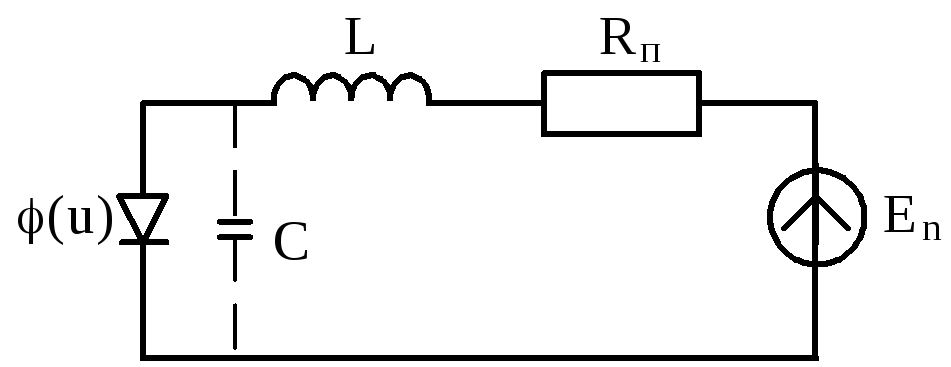 Пример
3.2. Для иллюстрации метода линеаризации
и критерия Рауса – Гурвица рассмотрим
схему с туннельным диодом (рис.3.19),
способную при определенных условиях
усиливать или генерировать колебания.
Пример
3.2. Для иллюстрации метода линеаризации
и критерия Рауса – Гурвица рассмотрим
схему с туннельным диодом (рис.3.19),
способную при определенных условиях
усиливать или генерировать колебания.
Рис.3.19. Нелинейная цепь, содержащая туннельный диод
Емкость С может быть как паразитной, так и включенной в схему.
М оделирующая
схема туннельного диода, упрощенная –
учитывающая только его нелинейные
свойства, а также более общая, учитывающая
потери в проводниках и их индуктивные
свойства представлены на рис.3.20.
оделирующая
схема туннельного диода, упрощенная –
учитывающая только его нелинейные
свойства, а также более общая, учитывающая
потери в проводниках и их индуктивные
свойства представлены на рис.3.20.
А б с
Рис.3.20.а − туннельный диод, б − схема замещения, учитывающая нелинейные свойства туннельного диода, с − схема замещения, учитывающая как нелинейные свойства туннельного диода, так и паразитные потери в проводниках, а также магнитные своиства проводников.
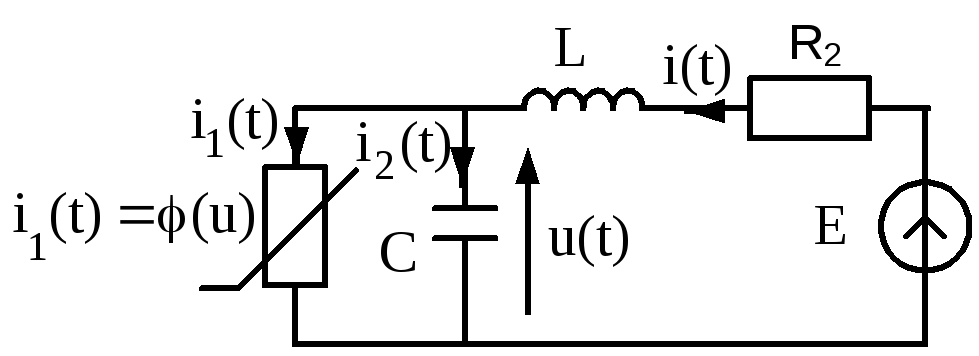
Рис.3.21. Эквивалентная схема для режима колебаний с учетом
нелинейных свойств туннельного диода
Для составления уравнений, описывающих колебания в такой схеме, используем оба закона Кирхгофа. Для этого введем обозначения: ток протекающий в неразветленной части схемы (рис.3.21) − i(t), а напряжение, на параллельно включенных элементах − u(t). Тогда, используя законы Кирхгофа, получаем:
 .
(3.27)
.
(3.27)
Используя уравнение связи для постоянной емкости, запишем ток i2(t) в виде:
![]() .
.
С учетом того, что ток через туннельный диод определяется его нелинейной вольтамперной характеристикой, запишем:
![]() .
.
Подставляя токи i1(t) и i2(t) в первое уравнение системы (3,27), получим нелинейную систему дифференциальных уравнений:
 .
(3.28)
.
(3.28)
В
соответствии с алгоритмом (рис.3.18), на
данном этапе, необходимо составить
эквивалентную схему для исследования
режима покоя. Режим покоя – это режим,
при котором токи и напряжения являются
постоянными величинами, т.е.
![]() одновременно. А это значит, что емкость
и индуктивность для исследования режима
постоянного тока в схеме (рис.3.21) не
учитываются (через емкость постоянный
ток не протекает, а индуктивность для
постоянного тока простой проводник).
одновременно. А это значит, что емкость
и индуктивность для исследования режима
постоянного тока в схеме (рис.3.21) не
учитываются (через емкость постоянный
ток не протекает, а индуктивность для
постоянного тока простой проводник).
П оэтому
эквивалентная схема режима постоянного
тока имеет вид (рис.3.22).
оэтому
эквивалентная схема режима постоянного
тока имеет вид (рис.3.22).
Рис.3.22. Эквивалентная схема, для режима покоя
Если (R2=Rq+Rн), то состояние цепи (рис.3.22) описывается нелинейной системой уравнений:
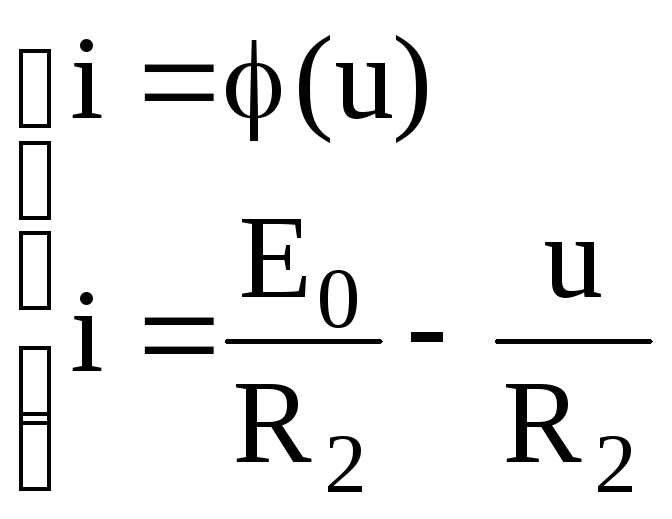 .
(3.29)
.
(3.29)
Решение данной системы нелинейных алгебраических уравнений можно найти либо графическим методом (рис.3.23), либо численным. Первое уравнение системы (3.29) есть вольтамперная характеристика туннельного диода, второе уравнение – нагрузочная линия. Точки пересечения этих двух линий дают нам всевозможные значения точек покоя. Возможное расположение нагрузочных линий представлено на рис.3.23.
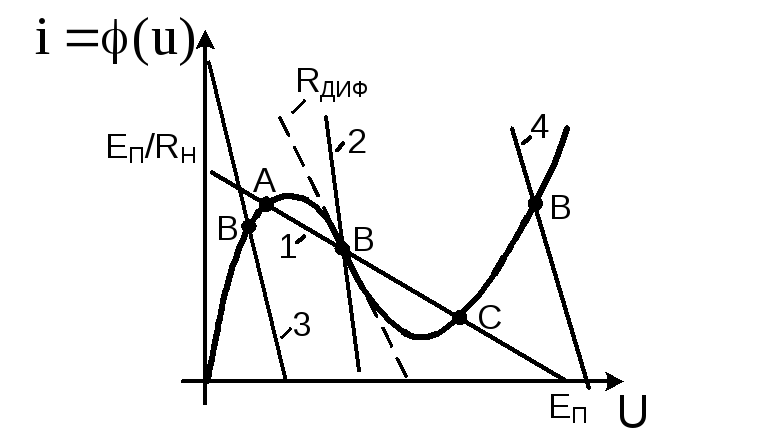
Рис.3.23. Графический способ решения уравнения (3.29)
В зависимости от параметров схемы (рис.3.23), нагрузочные линий могут пересекать вольтамперную характеристику четырьмя разными способами. Поэтому возможны четыре режима покоя в данной схеме. Для того, чтобы исследовать возможные колебания для каждого из этих случаев, необходимо в соответствии с алгоритмом найти дифференциальные параметры нелинейных элементов. В нашей схеме только один нелинейный элемент – туннельный диод. Он будет для режима малых отклонений от точек покоя заменен на дифференциальную проводимость. В соответствии с формулой (3.4) Gд определяется как тангенс угла наклона касательной к вольтамперной характеристике в точке покоя.
Для режима колебаний эквивалентная схема представлена на рис.3.24.
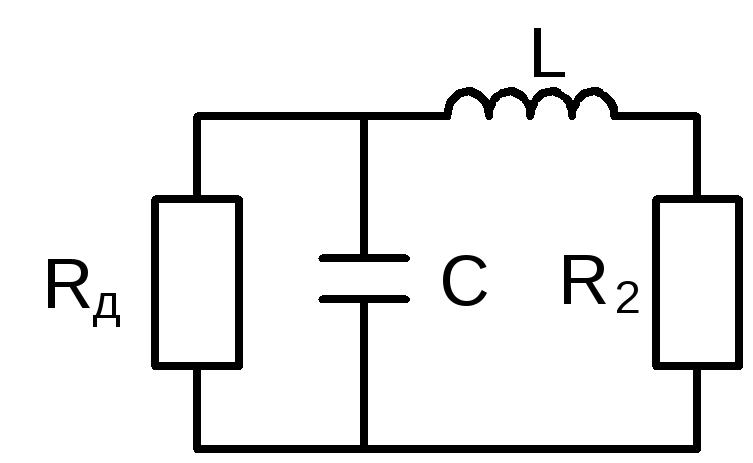
Рис.3.24. Эквивалентная схема для режима малых колебаний в схеме
на туннельном диоде
Для режима малых колебаний, т.к. все элементы теперь являются постоянными величинами, применимы методы теории линейных цепей. Например, составленное с помощью операторного метода уравнение малых колебаний в схеме на туннельном диоде примет вид:
![]() .
(3.30)
Правая часть
уравнения (3.30) может либо равняться
нулю, либо содержать источник, описывающий
воздействия на нашу схему.
.
(3.30)
Правая часть
уравнения (3.30) может либо равняться
нулю, либо содержать источник, описывающий
воздействия на нашу схему.
Характеристическое уравнение схемы (рис.3.24) определяется выражением:
p2LC + p(LG1диф + R2C) + R2G1диф + 1=0 (3.31) или
![]() .
(3.32)
.
(3.32)
Введем обозначения:
![]() и
и
![]() ,
(3.33)
,
(3.33)
тогда характеристический полином принимает вид
p2 + a1p + a2=0. (3.34)
Определитель Рауса–Гурвица, составленный из коэффициентов характеристического полинома (3.34), имеет следующий вид:
 .
(3.35)
.
(3.35)
Состояние цепи является устойчивым, если D1=a1>0 и D2=a1a2>0, т.е. если a1>0 и a2>0 одновременно. Из выражения (3.33) для коэффициента а2 получаем, что для устойчивости цепи должно выполняться следующее соотношение:
 >0.
(3.36)
>0.
(3.36)
Для дальнейшего рассмотрения колебаний в схеме на туннельном диоде необходимо конкретизовать режимы работы схемы.
Случай
1 − триггер. Рассмотрим пересечения
нагрузочной линии и вольтамперной
характеристики (рис.3.23), который в
качестве решения дает три точки покоя,
причем точка В, в отличие от точек А и
С, расположена на падающем участке
вольтамперной характеристики. Поэтому
для т.В R1диф<0,
а для т.А и т.С R1диф>0.
Поэтому для т.А и т.С выполняются
одновременно условия, что a1>0
и a2>0.
Следовательно в т.А и т.С схема находится
в устойчивых состояниях покоя. Рассмотрим
состояние покоя для т.В. Для этого
запишем, что
![]() .
Тогда из соотношения (3.36) для этой точки
покоя находим:
.
Тогда из соотношения (3.36) для этой точки
покоя находим:
 >0.
(3.37)
>0.
(3.37)
Для устойчивости рабочей точки по постоянному току должно выполняться условие
![]() .
(3.38)
.
(3.38)
Проверим,
выполняется ли условие (3.38). Для этого
рассмотрим вольтамперную характеристику
и нагрузочную линию (рис.3.25) для данного
случая. Как известно,
![]() ,
а
,
а![]() .
Из (рис.3.25) видно, что
.
Из (рис.3.25) видно, что![]() ,
поэтому
,
поэтому![]() ,
а следовательно
,
а следовательно![]() .
Из последнего неравенства следует, что
.
Из последнего неравенства следует, что![]() ,
т.е. условие (3.38) не выполняется.
Следовательно, в т.В состояние покоя
неустойчивое и цепь все время будет
стремиться выйти из данного неустойчивого
состояния.
,
т.е. условие (3.38) не выполняется.
Следовательно, в т.В состояние покоя
неустойчивое и цепь все время будет
стремиться выйти из данного неустойчивого
состояния.
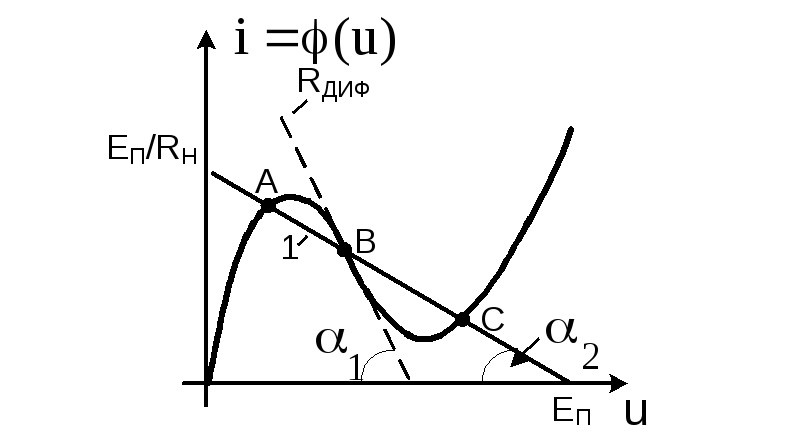
Рис.3.25. ВАХ туннельного диода, нагрузочная линия для трех точек
покоя, касательная к ВАХ на падающем участке, определяющая R1диф
Мы получили систему с двумя устойчивыми состояниями. Данная схема, при выбранных параметрах, может использоваться как триггер – схема с двумя устойчивыми состояниями (рис.3.26).

Рис.3.26. Схема триггера на основе схемы с туннельным диодом
В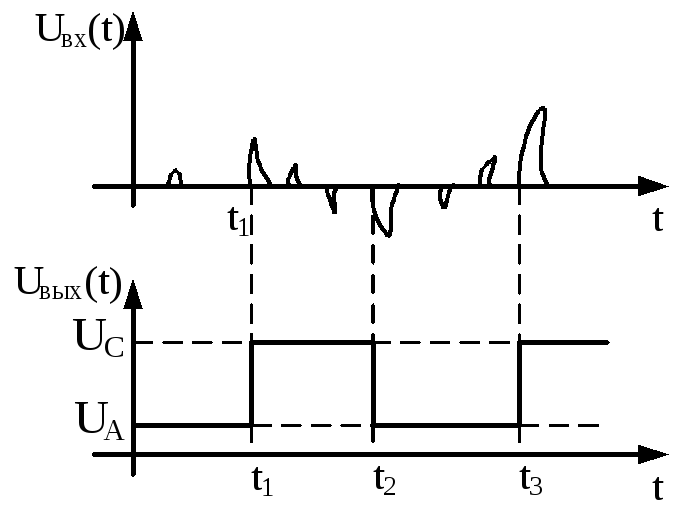 схеме рис.3.21 элементыL
и C
являются паразитными. Чем меньше L
и C,
тем быстрее осуществляется переход из
одного устойчивого состояния в другое.
схеме рис.3.21 элементыL
и C
являются паразитными. Чем меньше L
и C,
тем быстрее осуществляется переход из
одного устойчивого состояния в другое.
Рис.3.27. Графики Uвх(t) и Uвых(t) для триггера на туннельном диоде
Рассматривая работу схемы (рис.3.26) необходимо отметить, если вначале у нас рабочая точка находилась в т.А (рис.3.25), то схема не будет реагировать на любые отрицательные импульсы, и только положительный импульс с амплитудой, которая сможет перевести рабочую точку за неустойчивую точку покоя − т.В, переведет схему во второе устойчивое состояние в − т.С. Аналогично, если рабочая точка находится в точке − т.С, до тех пор пока на вход не прийдет отрицательный сигнал, амплитудой, способной перевести состояние системы за точку покоя − т.В, цепь не будет реагировать на любые импульсы. Если величина амплитуды отрицательного импульса будет достаточна для изменения состояния системы, на триггере установится устойчивое состояние в точке − т.А.
Случай 2. Рассмотрим случай когда существует только одна точка покоя − т.В (рис.3.23), расположенная на падающем участке вольтамперной характеристики. На рис.3.28 показано прохождение нагрузочной линии и касательной к вольтамперной характеристики в точке покоя.
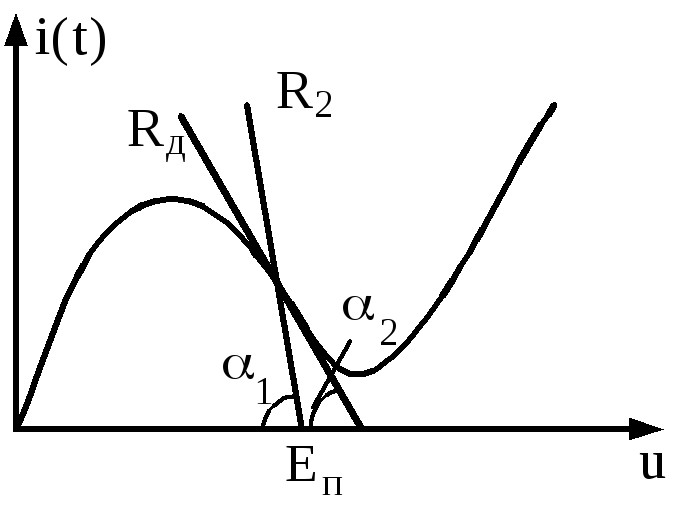
Рис.3.28. ВАХ туннельного диода и нагрузочная линия для одной точки
покоя на падающем участке, касательная к ВАХ, определяющая R1диф
Как
и для первого случая, рассмотрение
начнем с коэффициента а2.
Т.к. точка покоя находится на падающем
участке ВАХ, то
![]() .
Рассматривая
рис.3.28, можно сделать вывод, что
.
Рассматривая
рис.3.28, можно сделать вывод, что
![]() ,
т.к.
,
т.к.![]() и следовательно,
и следовательно,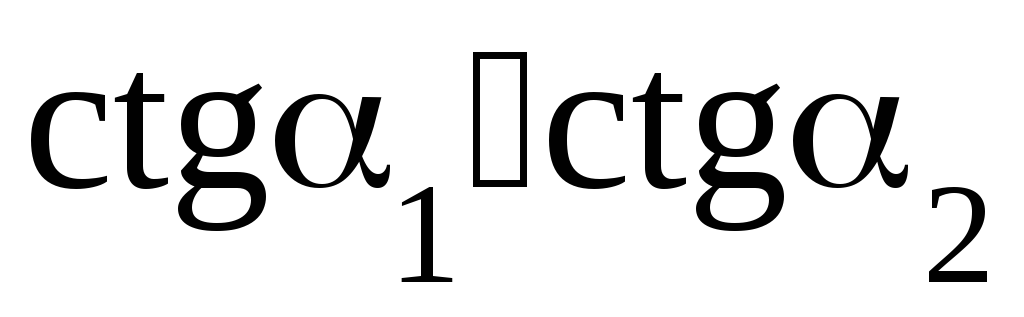 .
Поэтому
.
Поэтому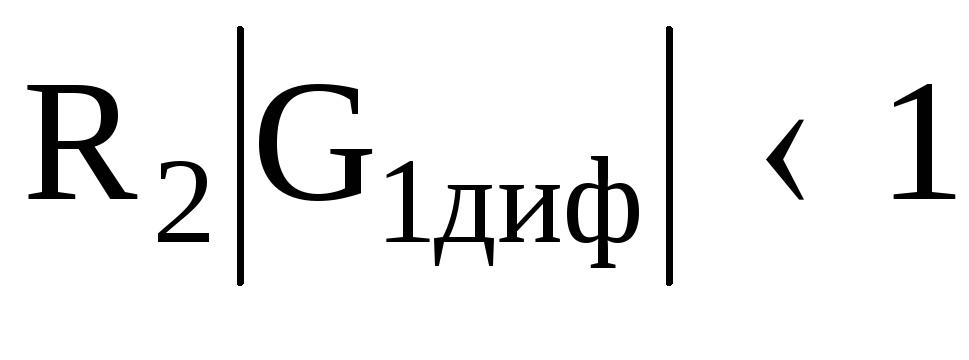 ,
а из (3.33) следует, что
,
а из (3.33) следует, что .
Следовательно сделать вывод о поведении
системы можно из рассмотрения коэффициента
а1.
В зависимости от параметров определяюших
коэффициент а1,
он может быть как больше, так и меньше
нуля. Рассмотрим различные варианты
схем, которые при этом реализуются.
.
Следовательно сделать вывод о поведении
системы можно из рассмотрения коэффициента
а1.
В зависимости от параметров определяюших
коэффициент а1,
он может быть как больше, так и меньше
нуля. Рассмотрим различные варианты
схем, которые при этом реализуются.
Случай
2а
− регенеративный усилитель.
Пусть
 ,
тогда из выражения (3.33) для коэффициентаa1
получаем, что а1>0,
т.к.
,
тогда из выражения (3.33) для коэффициентаa1
получаем, что а1>0,
т.к.
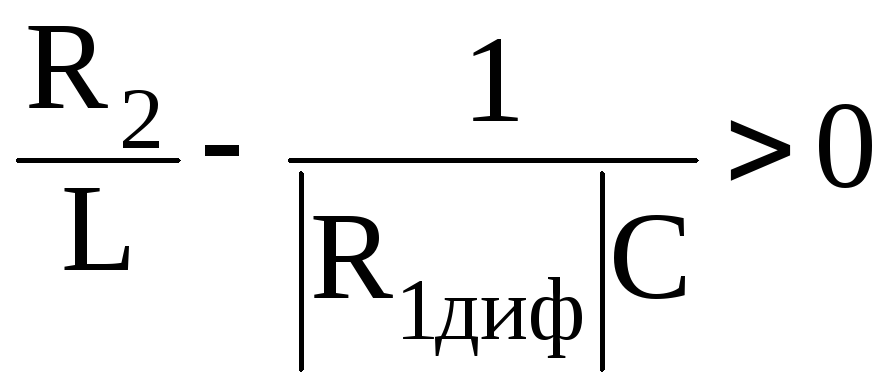 ;
(3.39)
;
(3.39)
т.е.
![]() .
(3.40)
.
(3.40)
Учитывая,
что
![]() -
эквивалентное сопротивление параллельного
контура при резонансе, тогда условие
устойчивости запишем в виде:
-
эквивалентное сопротивление параллельного
контура при резонансе, тогда условие
устойчивости запишем в виде:
![]() .
(3.41)
.
(3.41)
Т.к. коэффициенты а1>0 и а2>0 одновременно, то из критерия устойчивости Раусса-Гурвица следует, что схема в этом случае устойчива.
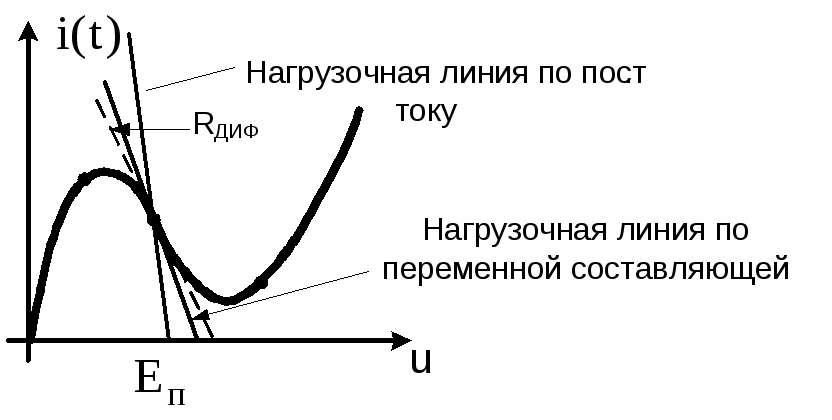

Рис.3.29. Графики ВАХ туннельного диода, нагрузочных линий для
постоянной и переменной составляющей
На
рис.3.29 представленно расположение
нагрузочной линии по переменному и
постоянному току, а также пунктиром
проведена линия касательная к ВАХ
туннельного диода, которая определяет
величину
![]() .
Если параметры схемы такие, что корнями
характеристического полинома является
пара комплесно-сопряженных корней (а
это возможно когда емкость С велика),
расположенные в левой полуплоскости
оператора
.
Если параметры схемы такие, что корнями
характеристического полинома является
пара комплесно-сопряженных корней (а
это возможно когда емкость С велика),
расположенные в левой полуплоскости
оператора![]() (рис.3.30), тогда колебания будут
(рис.3.30), тогда колебания будут
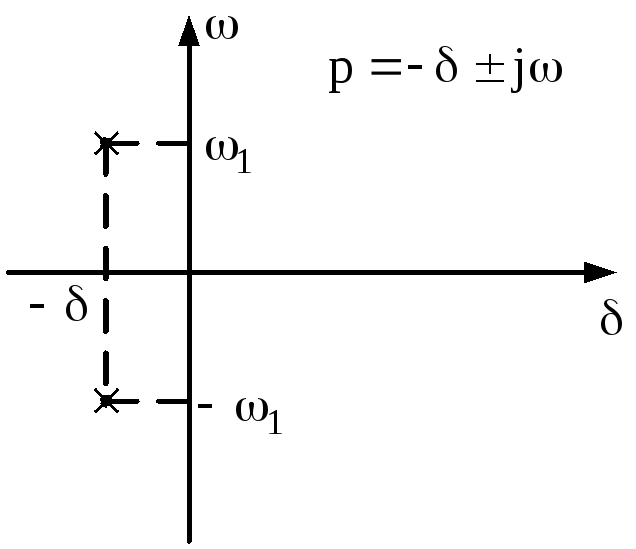
Рис.3.30 Расположение корней, для режима усиления колебаний
затухающими и иметь следующий вид (рис.3.31):
![]() .
(3.42)
.
(3.42)
В рассмотренном случае, имеет место регенерация, т.к. наличие отрицательной проводимости G1диф приводит к уменьшению потерь в схеме на туннельном диоде. Поэтому, для этого случая возможно получить усиление сигнала, а схема будет представлять собой регенеративный усилитель колебаний (рис.3.32).
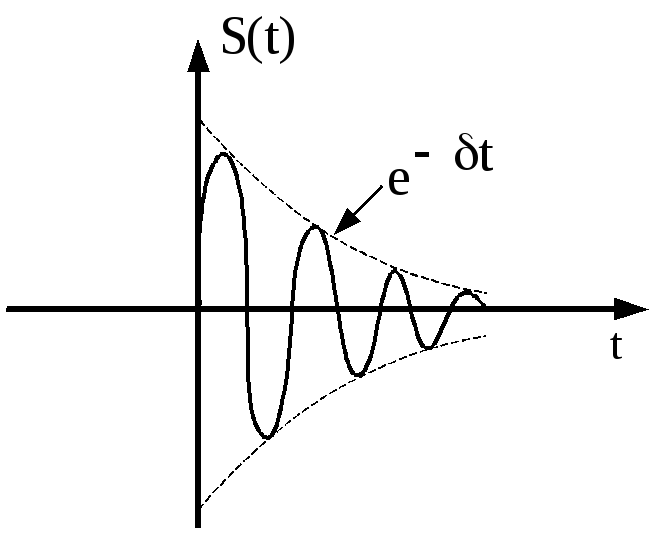
Рис.3.31. Закон изменения сигнала в регенеративном усилителе на
туннельном диоде
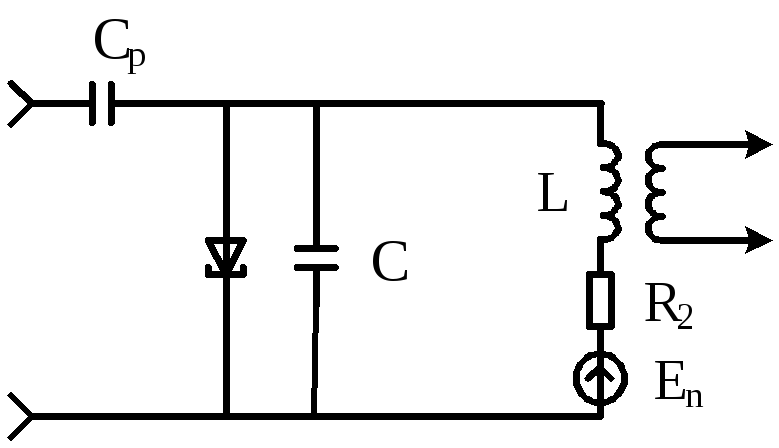
Рис.3.32. Схема регенеративного усилителя на туннельном диоде
Если рассмотренную цепь использовать для усиления колебаний, необходимо обеспечить устойчивость и положения рабочей точки, и колебаний.
Если
цепь использовать для генерирования
колебаний, необходимо обеспечить
устойчивость рабочей точки и неустойчивость
колебаний
![]() .
Следует заметить, что оба режима
использования схемы требуют выполнения
условияR2<|R1диф|.
.
Следует заметить, что оба режима
использования схемы требуют выполнения
условияR2<|R1диф|.
Случай 2б − генератор гармонических колебаний. Считаем, что как и в предыдущем случаи единственная точка покоя располагается на падающем участке ВАХ туннельного диода (рис.3.28), поэтому коэффициент а2>0. Пусть теперь параметры схемы такие, что обеспечивается выполнение следующего соотношения:
![]() ,
,
тогда из равенства (3.33) следует, что а1<0. В соотвествии с критерием Раусса-Гурвица, система стала неустойчивой. Если С велико, то корнями характеристического полинома V(p) будет пара комплексно-сопряженных корней с положительной действительной частью
![]() .
.
Поэтому на комплексной плоскости оператора p=δ+jω корни полинома V(p) будут распологаться в правой полуплоскости (рис.3.33), а решение для колебаний на начальной стадии (пока колебания малы и применим метод линеаризации) будут иметь нарастающий характер (рис.3.34).
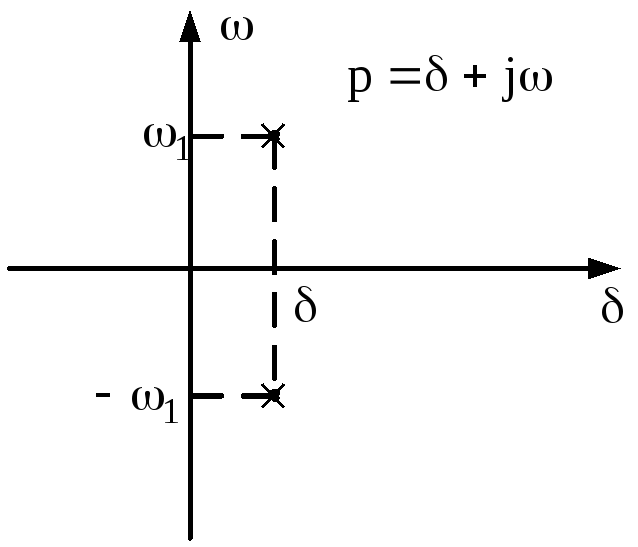
Рис.3.33. Расположение корней характеристического полинома на
плоскости оператора р для автогенератора гармонических колебаний

Рис.3.34. Начальнай стадия развития колебаний в автогенераторе
гармонических колебаний
Закон развития колебаний в автогенераторе на начальной стадии имеет следующий вид:
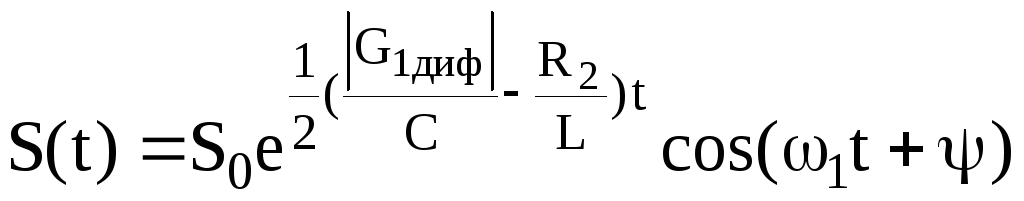 .
(3.43)
.
(3.43)
Колебания в автогенераторе не могут нарастатить до бесконечной величины. За счет нелинейных свойств вольтамперной характеристики туннельного диода, произойдет ограничение нарастания амплитуды колебаний автогенератора − установятся стационарные колебания. Метод линеаризации дает правильное решение только для начальной стадии развития колебаний, пока амплитуда мала. Как видно из соотношения (3.43), для возникновения режима автоколебаний необходимо устремить R2 к нулю. Вольтамперная характеристика туннельного диода, при расположении точки покоя на падающем участке ВАХ, дает положительную внутреннюю обратную связь. Поэтому схема автогенератора гармонических колебаний (рис.3.35), для получения колебаний не требует создания дополнительной обратной связи.

Рис.3.35. Схема автогенератора гармонических колебаний на туннельном
диоде
Случай 2в − генератор релаксационных колебаний (мультивибратор). Пусть, как и в предыдушем случае, выполняется следующее соотношение:
 ,
,
тогда из равенства (3.33) следует, что а1<0 и а2>0. Следовательно, система остается не устойчивой. Считаем, что R2=0, а емкость С − мала. В этом случае корни характеристического полинома будут действительными и располагаются в правой полуплоскости (рис.3.36).

Рис.3.36. Расположение корней характеристического полинома для
схемы на туннельном диоде − мультивибратора
Закон развития колебаний в автогенераторе релаксационных колебаний на начальной стадии имеет следующий вид:
![]() .
(3.44)
.
(3.44)
Это быстро нарастающие колебания, поэтому в этом положении рабочая точка не может находиться − возникнут автоколебания релаксационного типа. Схема автогенератора релаксационного типа на туннельном диоде − мультивибратора, представлена на рис.3.37. Здесь учтено, что для возникновения колебаний необходимо R2 и C устремить к нулю.
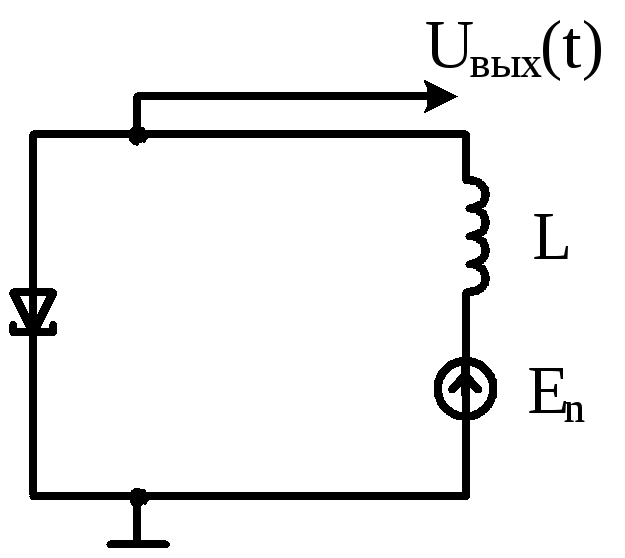
Рис.3.37. Схема мультивибратора на туннельном диоде
Для того, чтобы построить эпюры напряжения u(t) и тока i(t), рассмотрим (рис.3.38), на котором представлены графики ВАХ туннельного диода и нагрузочная линия, соответствующие режиму возникновения автоколебаний релаксационного типа. Представим, что момент времени t=0, совпадает с моментом времени подачи напряжения питания Eп на схему (рис.3.37).
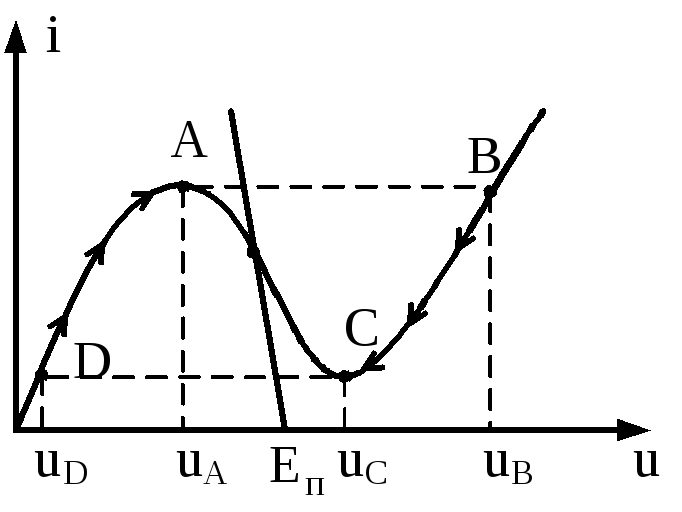
Рис.3.38. ВАХ и нагрузочная линии для схемы мультивибратора
на туннельном диоде
В
момент времени t=0
напряжение Eп
возникнет на индуктивности L,
ток через индуктивность L
начнет нарастать по экспоненциальному
закону (рис.3.39) до величины равной
![]() ,
время, за которое произойдет процесс
нарастания тока до указанной величины,
определяетсяRg
и L.
Т.к. ток, протекающий через индуктивность,
совпадает с током, протекающим через
туннельный диод, то рабочая точка начнет
смещаться по ВАХ туннельного прибора
от начальной величины i=0
и u=0
к точке А расположенной на ВАХ туннельного
прибора.
,
время, за которое произойдет процесс
нарастания тока до указанной величины,
определяетсяRg
и L.
Т.к. ток, протекающий через индуктивность,
совпадает с током, протекающим через
туннельный диод, то рабочая точка начнет
смещаться по ВАХ туннельного прибора
от начальной величины i=0
и u=0
к точке А расположенной на ВАХ туннельного
прибора.

Рис.3.39. Эпюры тока и напряжения для схемы мультивибратора
на туннельном диоде
Ток и напряжение на туннельном диоде будут соответствовать эпюрам (рис.3.39) от момента времени t=0 до t=t1. В момент, когда напряжение на туннельном диоде достигнет величины uA, произойдет пробой туннельного диода. Его сопротивление резко возрастет и напряжение на туннельном диоде достигнет величины равной uB. Рабочая точка перескочит на другую ветвь ВАХ туннельного диода. Напряжение на туннельном диоде превысит напряжение источника uB>Eп (рис.3.38), и начнется процесс перезаряда индуктивности L. Рабочая точка начнет смещаться по ВАХ туннельного диода от т.В к т.С, а эпюры напряжения и тока располагаются от момента времени t1 до момента t2 (рис.3.39). В момент времени t2 рабочая точка сместится по ВАХ в т.С. В этот момент времени произойдет резкое уменьшение сопротивления туннельного диода, рабочая точка перескочит в точку D, а напряжение на туннельном диоде станет равным uD. Теперь напряжение на туннельном диоде опять стало меньше напряжения питания uD<Eп, начнется новый процесс заряда индуктивности L, рабочая точка начнет смещаться от точки D к т.А, а эпюры напряжения, соответствующие этому процессу, расположены от моментов времени t2 до t3 (рис.3.39). Процесс будет повторяться сначала. Мы получили мультивибратор напряжение и ток на котором представлены на (рис.3.39).
Случай 3 – одновибратор (формирователь положительных импульсов). Рассмотрим вариант, когда сушествует одна точка, покоя, распологающаяся на нарастающем участке ВАХ туннельного диода (рис.3.40).
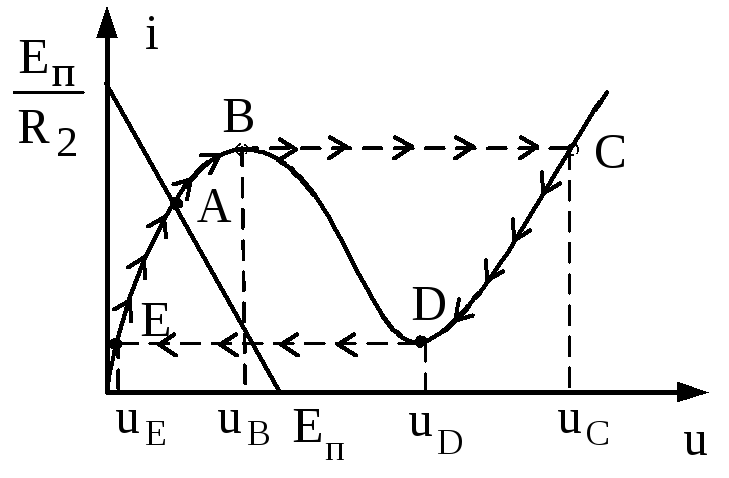
Рис.3.40. ВАХ и нагрузочная линии для схемы одновибратора
на туннельном диоде
Т.к. рабочая точка А находится на возростающем участке ВАХ туннельного диода, то G1диф>0, поэтому из равенства (3.33) следует, что а1>0 и а2>0. Следовательно, из критерия Раусса-Гурвица следует, что система в точке покоя т.А устойчива и будет там находиться сколь угодно долго. В случае, когда L велико, а C мало мы можем получить одновибратор или недовозбужденный мультивибратор.
 Схема
одновибратора показана на (рис.3.41).
Схема
одновибратора показана на (рис.3.41).
Рис.3.41. Схема одновибратора на туннельном диоде
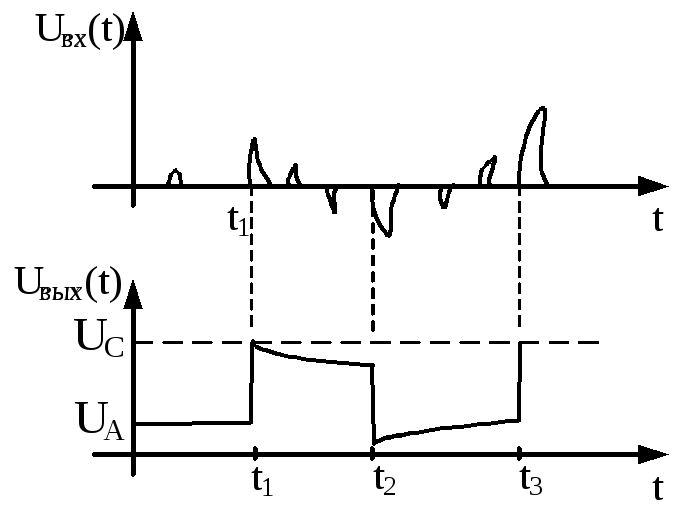
Рис.3.42. Эпюры напряжений одновибратра на туннельном диоде
При подаче на вход схемы (рис.3.41) импульса отрицательной полярности, схема на него реагировать не будет, т.к. она находится в устойчивом состоянии покоя. При подаче на вход импульса положительной полярности, только при приходе импульса величиной достаточной, чтобы перевести рабочую точку за точку В, рабочая точка совершит один цикл по пути т.А → т.В → т.С → т.D → т.E → т.A. Таким образом, сформировался положительный прямоугольный импульс и теперь, только по приходу следуюшего прямоугольного импульса достаточной амплитуды, сформируется следующий прямоугольный импульс.
Случай 4 – одновибратор (формирователя импульсов отрицательной полярности). Еще одной разновидностью одновибратора, является случай 4 на (рис.3.23).

Рис.3.43. ВАХ и нагрузочная линия для схемы одновибратора
на туннельном диоде

Рис.3.44. Эпюры напряжений одновибратра на туннельном диоде
Так же как и в предыдущем случае, система устойчива. В соответствии с условиями критерия Раусса-Гурвица, т.к. G1диф>0, поэтому коэффициенты а1>0 и а2>0. Если на вход схемы рис.3.41 подать импульс отрицательной полярности, амплитудой достаточной для того, чтобы переместить рабочую точку, за точку В, рабочая точка пройдет по пути т.А → т.В → т.С → т.D → т.E → т.A и у нас сформируется прямоугольный импульс отрицательной полярности (рис.3.44). Система вернется в устойчивое состояние покоя т.А, и будет находиться там как угодно долго, пока следующий отрицательный импульс не приведет к новому формированию прямоугольного отрицательного импульса.
Метод линеаризации позволил выяснить условие, при котором в цепи могут возникнуть автоколебания, но этот метод не дает возможности определить амплитуду установившихся колебаний. С этой задачей справится метод гармоничной линеаризации.
