
- •Министерство образования и науки украины
- •Введение
- •Глава і Свободные и вынужденные колебания в линейных инвариантных динамических системах
- •§1.1.Преобразование Лапласа и его основные свойства
- •§ 1.2. Применение операторного метода для анализа процессов в цепях с сосредоточенными элементами
- •§1.3 Общий вид решения задачи анализа свободных колебаний в линейных цепях
- •§1.4 Общий вид решения задачи анализа прохождения сигнала через устойчивую линейную цепь
- •Алгоритм решения задач анализа вынужденных колебаний в электрических цепях
- •§1.5. Свободные колебания в динамических системах с распределенными элементами
- •§1.5.1. Классификация длинных линий
- •§1.5.2.Построение решений уравнений длинных линий (телеграфных уравнений) операторным методом
- •Глава іі Колебания в линейных параметрических системах Линейные параметрические цепи
- •§ 2.1. Изменение спектра входного сигнала при прохождении через линейные параметрические цепи
- •§ 2.2. Аксиоматика теории цепей в параметрическом случае
- •§2.3. Прохождение сигналов через параметрические r – цепи
- •§2.4. Прохождение сигнала через параметрические
- •§ 2.5. Процессы в параметрической колебательной системе с одной степенью свободы. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.5.1. Процессы в механической параметрической колебательной
- •§ 2.5.2. Энергетическое рассмотрение стационарных колебаний в системах с одной степенью свободы
- •§ 2.6. Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье
- •§ 2.7. Параметрическое усиление колебаний в одноконтурной системе. Синхронный режим. Асинхронный режим
- •§2.8. Параметрический генератор (параметрон)
- •§2.9. Двухконтурные параметрические системы
- •§2.9.1.Теорема Менли-Роу
- •§2.9.2 .Двухконтурный параметрический усилитель нерегененративного типа
- •§2.9.3 .Двухконтурный параметрический усилитель регененративного типа
- •§ 2.9.4 Параметрические умножение и деление частоты
- •§2.11. Некоторые приближенные методы исследования процессов в параметрических системах
- •§2.11.1. Метод «замороженного» параметра
- •§2.11.2. Алгоритм метода замороженного параметра для задачи о свободных и вынужденных колебаниях в параметрических цепях
- •§2.11.3 Метод последовательных приближений
- •§2.11.3. Метод вкб (Вентцеля-Крамера-Бриллюэна)
- •Глава ш Анализ колебаний в нелинейных цепях
- •§3.1. Нелинейные элементы цепей
- •§3.2 Аппроксимация характеристик нелинейных элементов
- •§3.3 Преобразование спектра колебаний нелинейной цепью
- •§3.4 Особенности задач анализа колебаний в нелинейных цепях
- •§3.5 Анализ колебаний в цепях, составленных из нелинейных активных сопротивлений
- •§3.6. Метод линеаризации
- •§3.7. Метод гармонической линеаризации (мгл)
- •§3.7.1. Эквивалентные параметры нелинейных элементов
- •§3.7.2. Автогенератор гармонических колебаний.
- •§3.8. Методы малого параметра. Метод последовательных приближений
- •§3.9. Метод медленно меняющихся амплитуд (ммма).
- •§3.10. Метод малого параметра. Исследование ммма колебаний в автогенераторе на туннельном диоде
- •§3.11. Метод фазовой плоскости
- •§3.11. 1.Метод фазовой плоскости. Метод изоклин
- •§3.11.2. Метод фазовой плоскости. Особые точки
- •§3.11.2.Исследование методом фазовой плоскости схемы на
- •§1.1. Преобразование Лапласа и его основные свойства 7
- •610077,М. Харків, пл. Свободи, 4.
- •610077,М. Харків, пл. Свободи, 4.
§3.11. Метод фазовой плоскости
Метод фазовой плоскости – графический метод, позволяющий качественно исследовать колебания в цепях, описываемые дифференциальными уравнениями второго порядка. Существует несколько вариантов методов фазовой плоскости, применяемые в зависимости от постановки задачи. Обобщением метода фазовой плоскости для случаев, когда колебания описываются уравнениями более высокого порядка (n › 2) является метод фазового пространства (n – мерного). Термин «фаза» в названии метода имеет смысл ″состояние″. Если дифференциальное уравнение имеет порядок n, тогда для определения конкретного решения, кроме общего вида решения, необходимо также располагать n − начальными условиями, например, f(t0), f(1)(t0), f(2)(t0), … f(n-1)(t0). Эти величины можно рассматривать в качестве n – координат фазового пространства. Начальные значения координат, т.е. условия для t = t0 определяют в фазовом пространстве точку. При изменении t от t0 значения всех величин – координат изменяются, т.е. во времени изменяется положение точки, описывающей состояние колебательного процесса (в соответствии с общим решением дифференциального уравнения).
Метод фазовой плоскости применяется для качественного анализа процессов установления колебаний в автогенераторе, а также для анализа вынужденных колебаний в нелинейных цепях.
В тех случаях, когда неприменим ни один из рассмотренных методов, а также другие количественные методы, единственным, позволяющим провести качественный анализ, является метод фазовой плоскости (пространства).
Основные
определения:
фазовой
плоскостью
называется координатная плоскость на
которой откладывается по оси абсцисс
– мгновенные значения самой функции,
описывающей колебания, а по оси ординат
– мгновенные значения производной той
же функции (например, q(t)
и i(t)
=
![]() илиi(t)
и
илиi(t)
и
![]() и т.д.).
и т.д.).
Поскольку
в реальных цепях не существует колебаний,
достигающих бесконечно больших величин,
все возможные состояния колебаний на
фазовой плоскости располагаются в
обозримой области при любых значениях
t
от t0
до
![]() .
.
Изображающей
точкой
М(х,у) называется точка фазовой плоскости
координаты которой определяют состояние
колебательного процесса, мгновенные
значения s(t)
и
![]() .
.
Фазовой траекторией называется путь движения изображающей точки по фазовой плоскости. Фазовая плоскость, заполненная фазовыми траекториями, определяющими поведение системы при любых начальных условиях, называется фазовым портретом. Скорость перемещения изображающей точки по фазовой траектории называется фазовой скоростью. В любой точке фазовой плоскости эта скорость направлена по касательной к фазовой траектории, а величина её выражается через скорость изменения координат
vx
=
![]() v
v![]() vф
=
vф
=
![]() .
.
Обычной
точкой фазовой плоскости
называется точка через которую проходит
одна фазовая траектория. Простой
особой точкой
называется точка через которую проходит
несколько траекторий, либо не проходит
ни одна. Этим точкам соответствуют
равновесные состояния цепей (систем).
В этих точках
![]() и
и
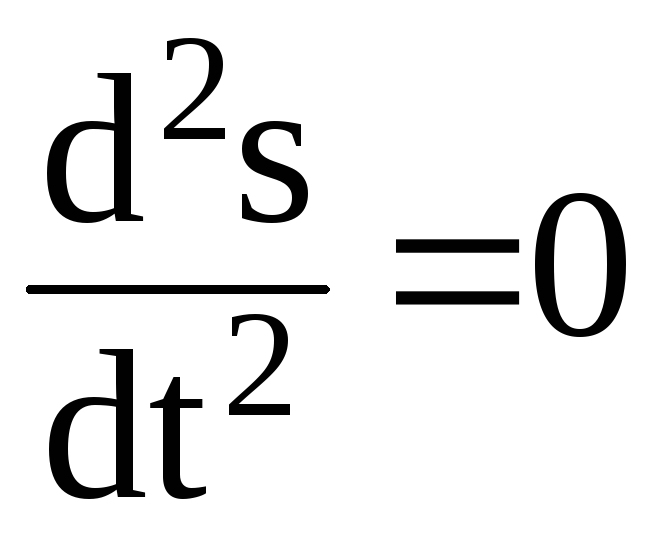 одновременно.
Количество
особых точек, их расположение на фазовой
плоскости и характер фазовых траекторий
в
их
окрестностях определяют характер
колебательных процессов.
одновременно.
Количество
особых точек, их расположение на фазовой
плоскости и характер фазовых траекторий
в
их
окрестностях определяют характер
колебательных процессов.
Кроме особых точек, существенными для определения характера процесса являются особые линии фазовой плоскости – предельные циклы и сепаратриссы.
Предельным циклом называется замкнутая фазовая траектория к которой, в пределе при t → ± ∞, стремится некоторое множество фазовых траекторий.
Сепаратриссы – линии, разделяющие фазовую плоскость на области притяжения к особым точкам.
Исследование колебаний в цепи методом фазовой плоскости сводится к построению фазовой траектории, соответствующей определенным начальным условиям. По фазовой траектории можно определить вид функции (график) описывающей колебательный процесс. Рассмотрим метод фазовой плоскости применительно к анализу колебаний в автогенераторе, описываемых уравнением
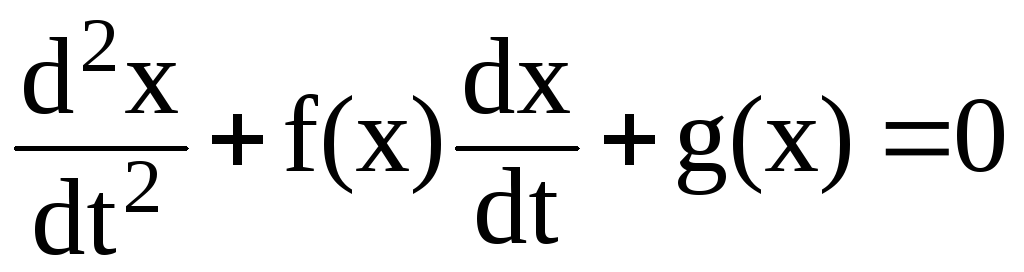 .
(3.107)
.
(3.107)
Преобразуем
это уравнение заменой
![]() в систему уравнений
в систему уравнений
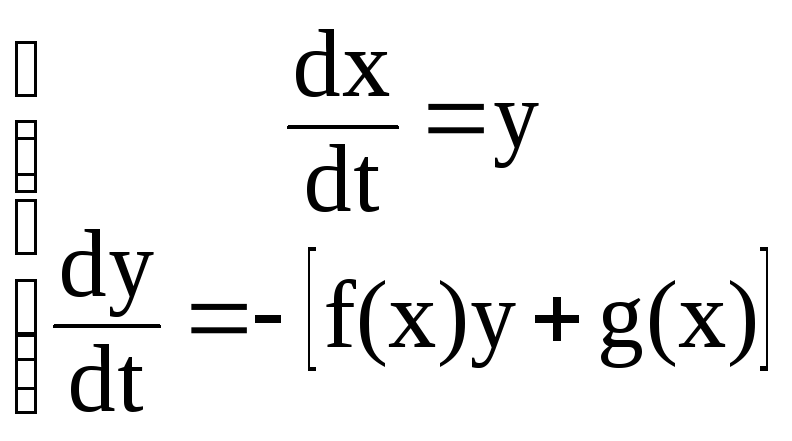 ,
(3.108)
,
(3.108)
и исключая время t из системы уравнений (3.108), получим
![]() .
(3.109)
.
(3.109)
Перейдем к уравнению, которое можно анализировать методом фазовой плоскости.
В самом общем виде нелинейные колебания определяются двумя уравнениями первого порядка
 ,
(3.110)
,
(3.110)
Причем, описание нелинейных колебаний в виде системы уравнений (3.110) более общее, чем с помощью одного уравнения (3.107).
