§ 2.6. Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье

В предыдущем параграфе мы рассмотрели энергетический способ исследования параметрических систем. Рассмотренный метод позволил вывести формулы, определяющие значение коэффициента модуляции при котором в колебательной системе возможно либо усиление колебаний, либо

стационарный режим, либо нарастающие колебания. Однако энергетический метод не может дать ответ, как будут изменяться ток и напряжение в параметрическом контуре.

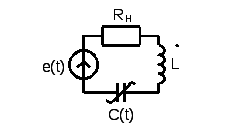
Рис.2.14. Параметрический колебательный контур

В данном параграфе рассматривается другой часто применяемый способ исследования колебаний в параметрических системах, описываемых дифференциальными уравнениями второго порядка.

Анализ процесса в рассматриваемом параметрическом контуре (рис.2.14) основан на сведении уравнений, описывающих колебания в контуре, к известным уравнениям, в данном случае к уравнению Матье:

(2.52)

Пусть параметрическая емкость колебательного контура изменяется по закону

. (2.53)

Данный закон изменения емкости выполняется, когда к варикапу приложено гармоническое воздействие.

Запишем с помощью МКТ дифференциальное уравнение параметрических колебаний в параметрической цепи (рис.2.14)

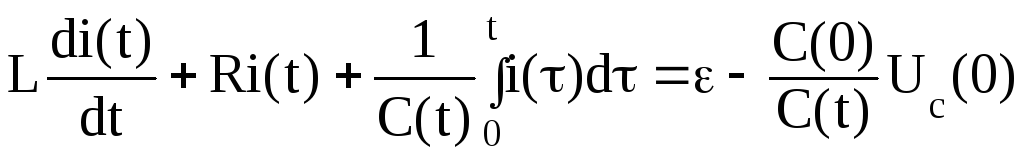. (2.54)

Мы получили интегро-дифференциальное уравнение. Чтобы получить дифференциальное уравнение сделаем замену переменных

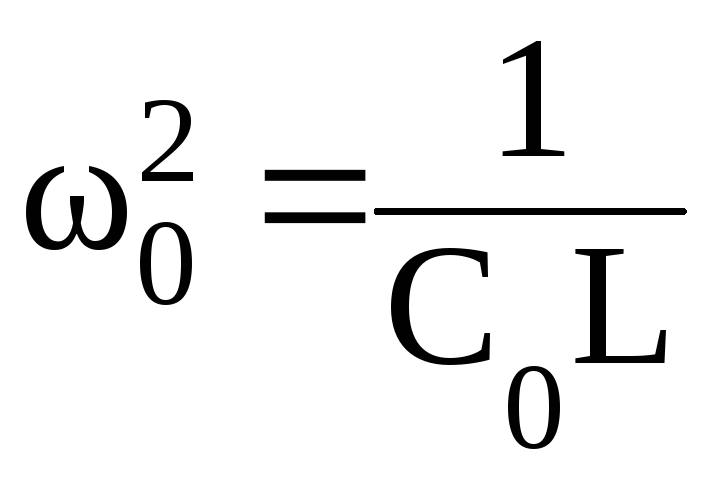, (2.55)

которая позволяет перейти к дифференциальному уравнению второго порядка в следующем виде

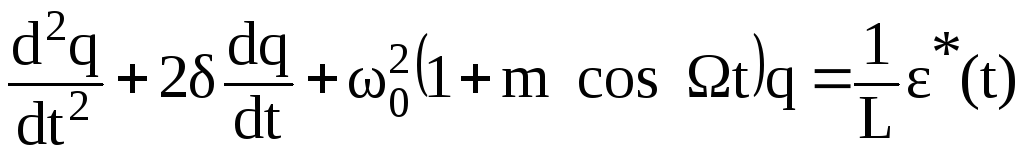. (2.56)

Для того чтобы избавиться от производной первого порядка в уравнении (2.56) сделаем следующую замену переменных:

Подставляя найденные выражения для q(t), и в дифференциальное уравнение (2.56), получаем

+,

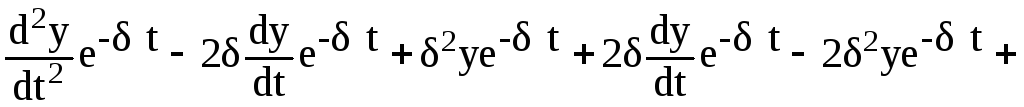
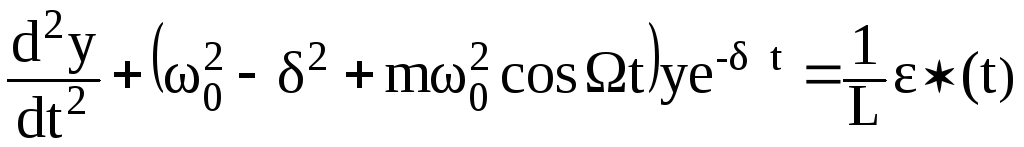. (2.57)

В уравнение (2.57) введем безразмерное время τ

; .

Подставим его в (2.57)

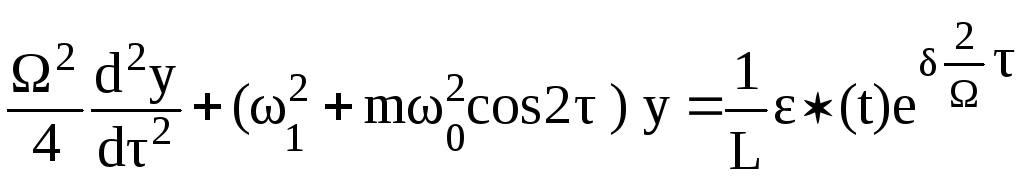. (2.58)

Введем следующие обозначения:

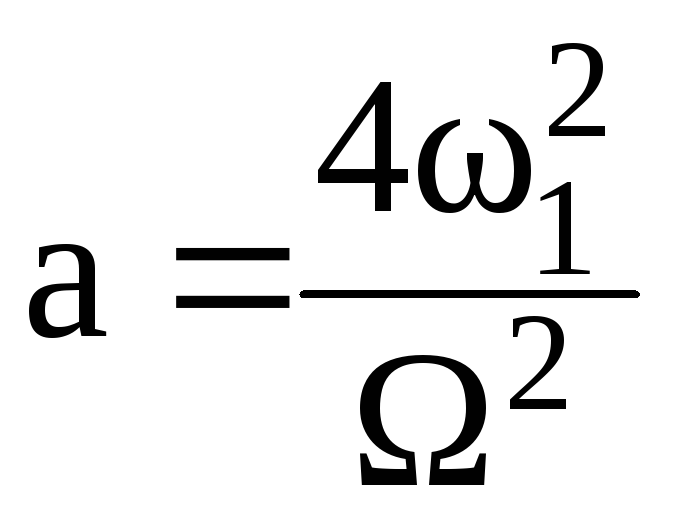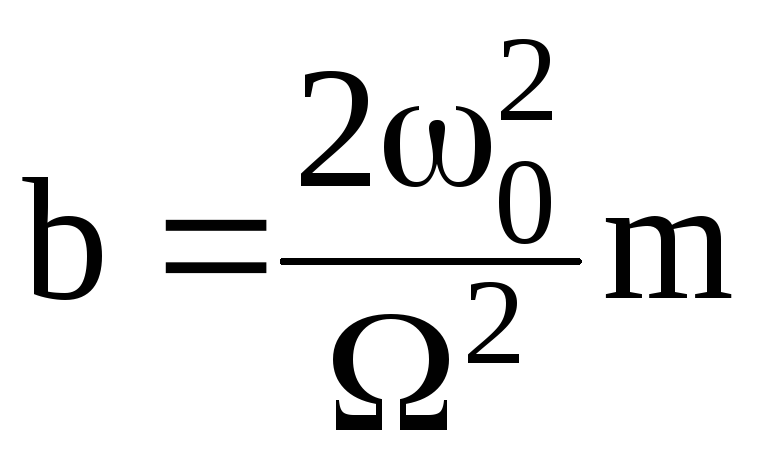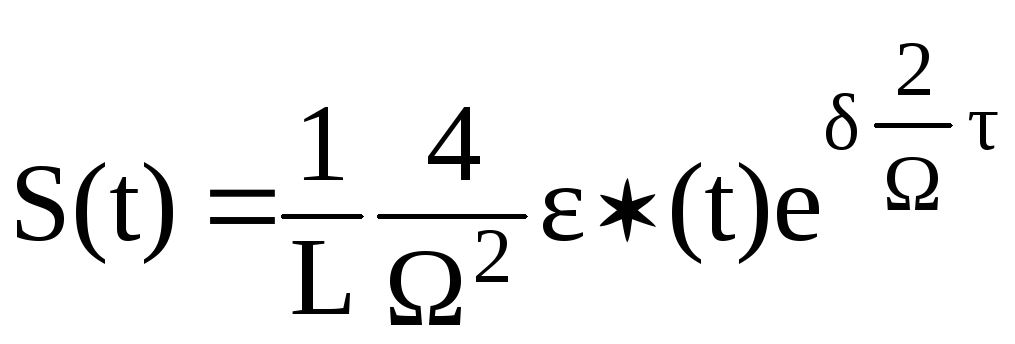; ;. (2.59)

Тогда уравнение колебаний (2.58) в параметрическом контуре (рис.2.13) примет вид:

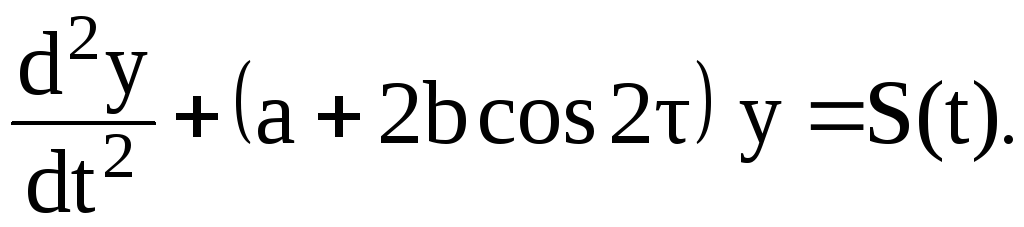(2.60)

Уравнение (2.60) является уравнением с периодическим коэффициентом, зависящим от времени τ, где a и b – положительные величины. Кроме того, из (2.59) видно, что b < a, т.к. m < 1.

Решение уравнения Матье строится с помощью теоремы Флоке, которая гласит, что для уравнений типа Хилла (коэффициенты которого являются периодическими функциями) решения есть почти периодические функции:

, (2.61)

где коэффициент К = const.

Отсюда следует, что функция удовлетворяет теореме Флоке, если φ(τ) периодическая функция. Уравнению (2.61) удовлетворяет и функция . Покажем на примере функции, что выполняется теорема Флоке:

.

Возникли периодические функции φ(τ) и , которые называют функциями Матье: φ()=φ(,a,b).

μ= μ(a,b) – некий коэффициент, зависящий от параметров a и b. Причем a и b – вещественные положительные числа, а может быть: либо вещественным, либо равно нулю, либо мнимым.

Т.к. функции у₁(τ) и у₂(τ) удовлетворяют теореме Флоке, решение уравнения Матье будет представляться как комбинация этих двух функций:

. (2.62)

Из вида решения (2.62) видно, что нас должен интересовать случай, когда μ= μ(a,b) - действительная величина любого знака, т.к. только в этом случае одно из слагаемых решения (2.62) будет нарастающей функцией. А это значит, что мы получили колебания с возрастающей амплитудой – возбуждение колебаний за счет энергии внесенной параметрической емкостью (параметрический генератор). Т.е. в этом случае вносимая энергия превышает потери, которые существуют в контуре. Следовательно, условием самовозбуждения колебаний в параметрическом контуре есть условие |μ= μ(a,b)|>0. Если μ= μ(a,b)=0, то мы получаем решения с постоянной амплитудой, т.е. вносимая энергия в колебательный контур параметрической емкостью равняется энергии потерь в нем. Таким образом можно сделать вывод, что в случае когда:

а) – функция описывает стационарные решения

б) - вещественная величина– решения расходятся и, следовательно, они описывают нарастающие колебания

в) - мнимая величина– решения будут сходящимися, а колебания затухающими.

Рассмотрим однородное уравнение Матье, в котором устремим коэффициент b к нулю

.

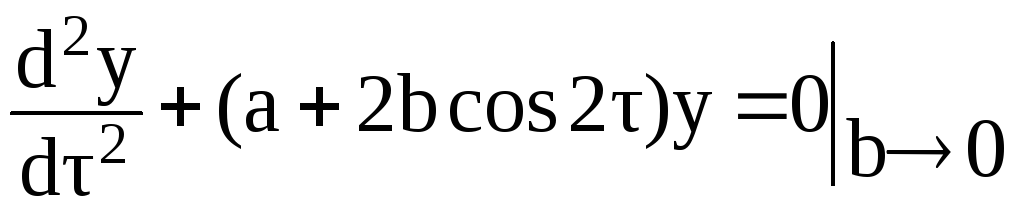Тогда уравнение примет вид:

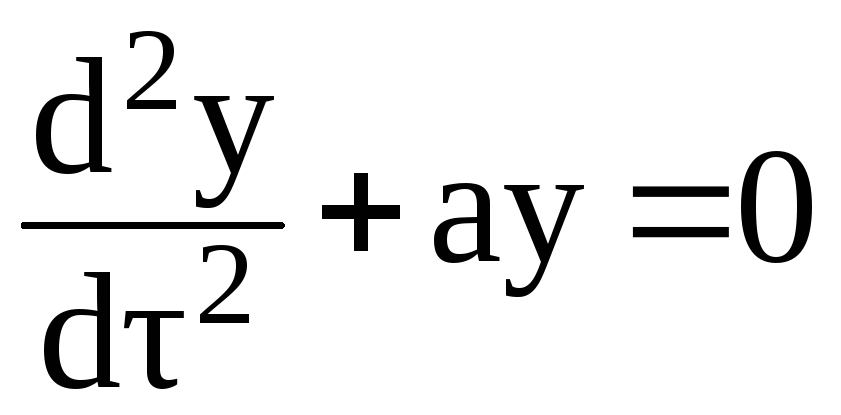
и его решение выражается через тригонометрические функции

.

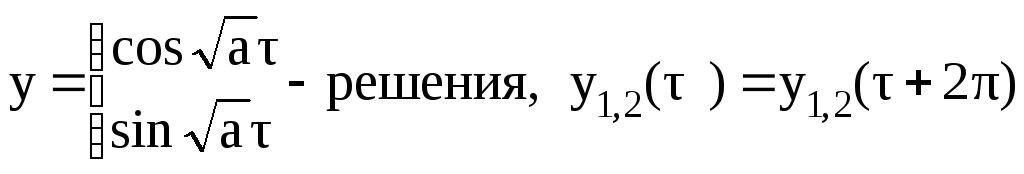Вид решения у(τ) для схемы рис.2.15.а не изменится (т.е. будет выполняться теорема Флоке) только в том случае, когда , гдеn любое целое число. Только в этом случае сдвиг фазы на приведёт к тому, что значение функцийне изменится.

Нахождение значений коэффициента в общем случае проблема. Поэтому строятся диаграммы значений параметров а иb, при которых решение для у(τ) будет иметь различный характер поведения в зависимости от значения коэффициента (см. рис.2.15.б). Зоны значений параметра μ(a,b) стягиваются к значениям оси абсцисс, в которых а=n², где n любое целое число. Внутри зон решение для колебаний будет иметь нарастающий характер, а само -действительное число. На границе зон в любом месте=0 – стационарные колебания функции. Вне зон коэффициент- мнимая величина и колебания являются затухающими.

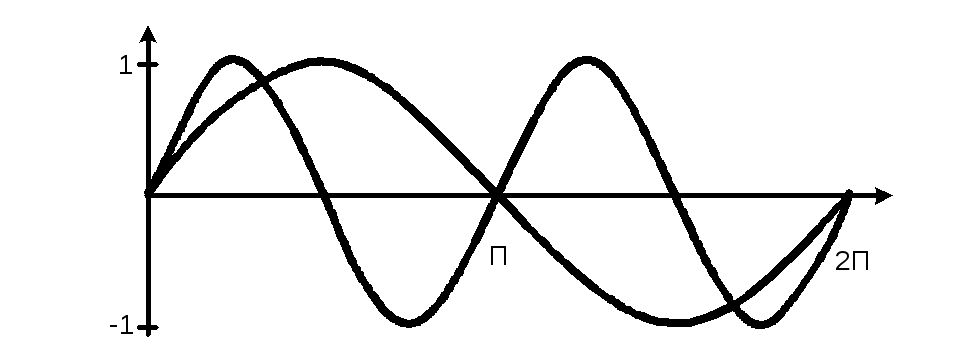
а) б)

Рис. 2.15. а) закон изменения периодической функции б) области

значений коэффициента

Как было показано ранее, при исследовании коэффициента модуляции с помощью энергетического метода, , поэтому из выражения (2.59) следует, что коэффициентb также мал. Поэтому можно предположить, что у(τ) не сильно отличается от тригонометрической функции (случай когда b =0) и решение для y(τ) можно записать в виде:

. (2.63)

С учетом того, что , находим: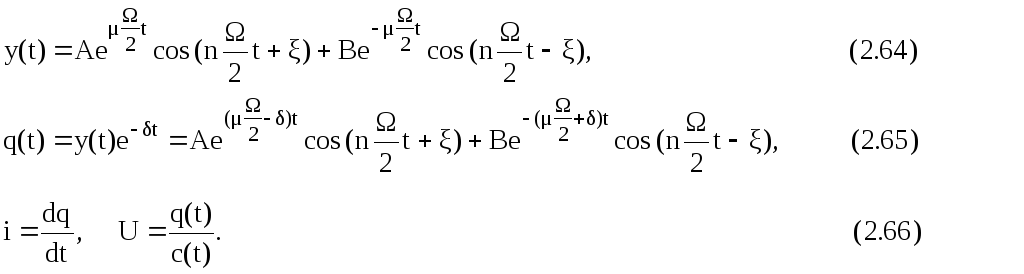Из формулы (2.64) следует, что зоны неустойчивости функцииq(t) располагаются внутри зон неустойчивостей для y(t) − рис.2.16.

Из уравнения (2.65) следует, что при выполнении условия ||>δ,будет нарастающей функцией. Это соответствует зонам, обозначенным пунктирными линиями.

b

a

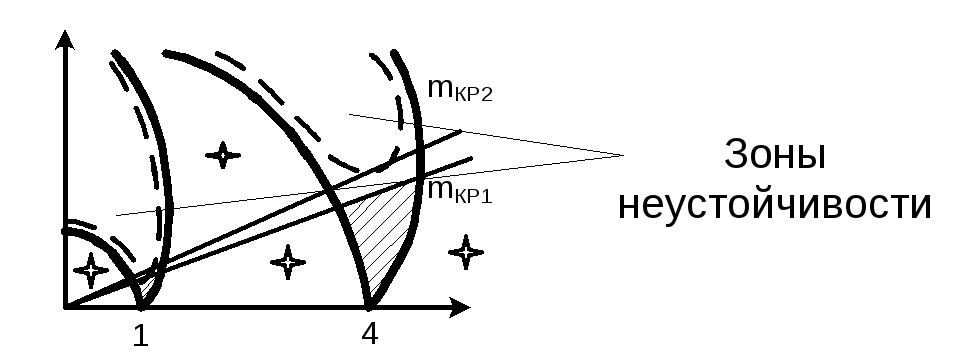
Рис. 2.16. Зоны неустойчивости для функций: у(t) - сплошная линия;

- пунктирная

Если частоты модуляции и накачки, а также параметр модуляции такие, что решения попадают в нижнюю часть зоны рис.2.16 – на графике эти зоны заштрихованы, то энергия отклика для превышает начальную энергию, но колебания все равно остаются затухающими - зона регенеративного усиления. Если решение попадает в верхнюю часть зоны, где вносимая энергия превышает энергию потерь - возникает режим автоколебаний. Касательная, проведенная к нижней точки каждой из зон, соответствует случаю стационарных колебаний. При этом энергия, вносимая в колебательный контур за счет параметрической емкостиC(t), равняется энергии потерь. Для этих случаев можно определить критическое значение параметра – m_кр, как тангенс угла наклона соответствующих касательных. Области, помеченные звездочками, не имеют практического значения, т.к. там происходит еще большее затухание.

Выводы. В целях получения параметрического усиления или возбуждения колебаний следует использовать такое соотношение параметров а и b (т.е. ω₀, иm), при котором решение соответствует областям неустойчивости. Если при этом коэффициент модуляции m меньше m_крn, в системе можно осуществить регенеративное усиление. Если же коэффициент модуляции m – больше m_крn,, в системе происходит параметрическое возбуждение нарастающих колебаний, которые в дальнейшем ограничиваются какими-либо нелинейными элементами, неизбежно существующими в цепях.