§2.4. Прохождение сигнала через параметрические

цепи первого порядка. Метод функции Туркина

К параметрическим цепям первого порядка относятся цепи, содержащие один энергоемкий элемент (индуктивность или емкость) и резистивный элемент, причем хотя бы один из элементов цепи является параметрическим. Уравнения, описывающие процессы в такой параметрической цепи, сводятся к дифференциальным уравнениям первого порядка с переменными коэффициентами и имеют следующий вид

+ a(t)*S = f(t) (2.25)

Известно, что такие дифференциальные уравнения, как правило, допускают непосредственное интегрирование и их решение можно представить в квадратурах. Однако очень часто полученное решение нельзя выразить в известных функциях, кроме того, его форма может не соответствовать конечным целям исследования. Например, полученное выражение в замкнутом виде трудно поддается спектральному анализу, проверке на устойчивость и т.д.

Общий подход к анализу параметрических цепей первого порядка основан на традиционных методах решения дифференциальных уравнений и заключается в том, что сначала ищется решение однородного уравнения

+ a(t)*S = 0, (2.26)

а затем произвольная постоянная С заменяется на С(t), которая определяется после подстановки решения S_св(t) однородного уравнения в искомое (метод Лагранжа).

Однако, так как получаемые этим методом решения не всегда удобны для анализа, в радиотехнике разработаны специальные приемы и методы решения указанных уравнений. Наибольший практический интерес представляет анализ параметрических цепей при постоянных и моногармонических воздействиях, так как все другие воздействия можно свести к суперпозиции этих воздействий. Рассмотрим примение метода и функий Туркина на следующем примере.

Пример 2.4. В цепи, изображенной на рис 2.7., генератор развивает напряжение e(t) = U₀ e^iωt, параметрическая емкость меняется по закону

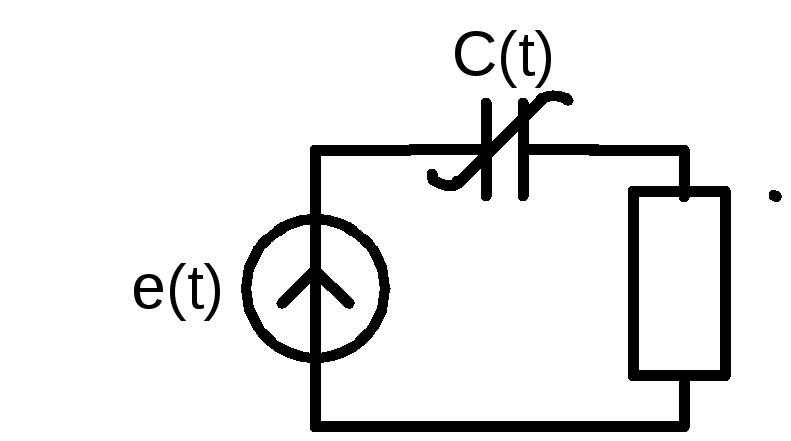C(t) = , где μ – коэффициент

модуляции емкости. Найти закон изменения и

определить спектральные составляющие тока в

цепи.

Рис.2.7. Параметрическая RC- цепь

Уравнение для тока в цепи рис.2.7. имеет вид:

R i + 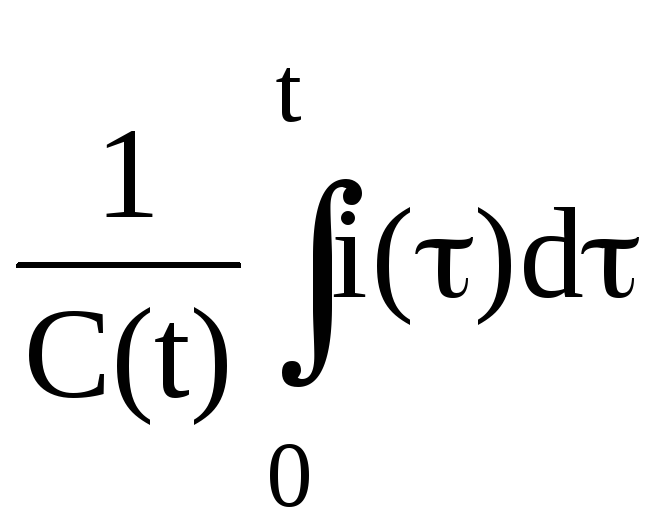=e(t) (2.27)

и является интегродифференциальным уравнением.

Для того чтобы привести наше уравнение к дифференциальному уравнению первого порядка запишем его относительно заряда, который связан с током по закону i(t) = . Кроме того, подставим выражения дляC(t) и e(t) в интегро-дифференциальное уравнение:

R + 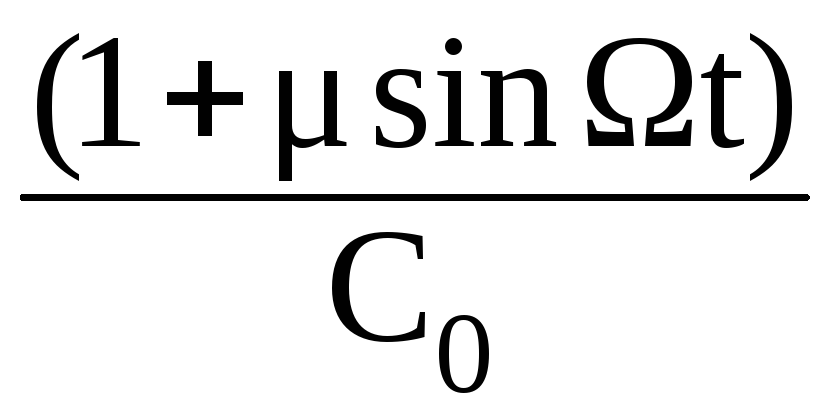q = U₀ e^iωt, (2.28)

где x(τ) = q(τ), τ = Ωt, a =, b =, p =.

Общее решение данного уравнения известно:

x(τ) = e ^- [ e dτ + C ] .

Интегралы в показателях экспоненты являются табличными

x(τ) = .

Оставшийся интеграл не берется в известных функциях. Воспользуемся следующим разложением

= (2.29)

и, обозначив z = iaμ , перепишем последнее выражение в форме

x(τ) = J_-n(z) e [a ] =

= C + a. (2.30)

Постоянная С определяется из начальных условий. Первый член этого выражения описывает свободный процесс, а второй – установившийся. Рассмотрим произведение рядов во втором члене:

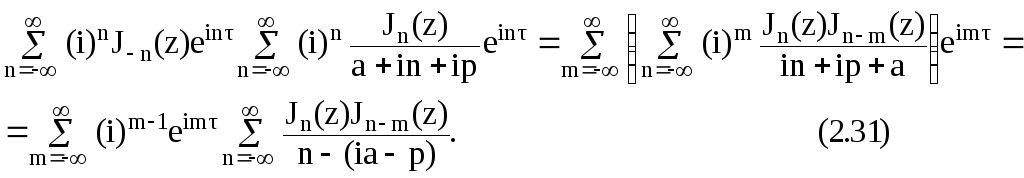
Обозначив перепишем общее решение в виде

,

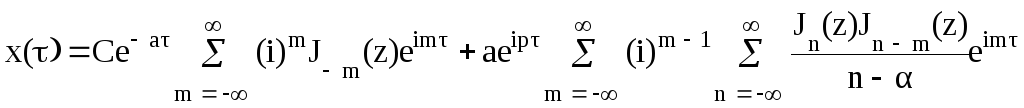а затем

, (2.32)

где . (2.33)

Функции 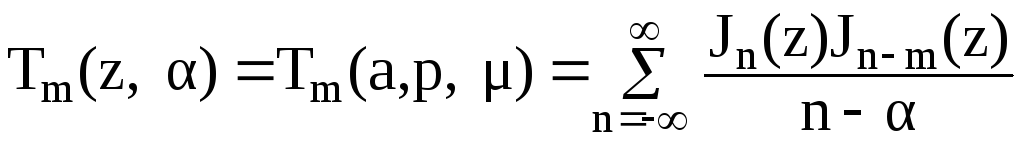(2.34)

введены В.К.Туркиным и носят его имя, для этих функций составлены таблицы при различных значениях параметров .

Для установившегося режима окончательное выражение принимает вид:

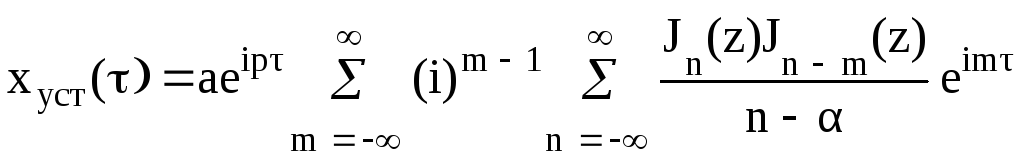. (2.35)

Свободный процесс описывается выражением

, (2.36)

где постоянная С определяется из условия q_св(0) = q₀.

Полученные выражения дают полное решение задачи для установившегося режима как при гармоническом воздействии вида cosω₀t, sin ω₀t, e^±it, так и при постоянном воздействии U₀ = const, причем решение записывается в виде суммы гармонических составляющих.

Пример 2.5. Рассмотрим расчет установившегося процесса в случае, когда параметр может быть представлен любой периодической функцией. В этом случае колебания будут описываться дифференциальным уравнением первого порядка с параметрическим коэффициентом, изменение которого представляется любой периодической функцией

, (2.37)

где , что допускает его разложение в ряд Фурье. Считаем, что параметрический коэффициент может быть представлен в виде, тогда общее решение имеет вид

. (2.38)

Введем следующие обозначения

а , (2.39)

тогда получаем , (2.40)

Т.к. ипериодические функции, их можно разложить в ряд Фурье

; (2.41)

Тогда общий вид решения (2.40) примет вид:

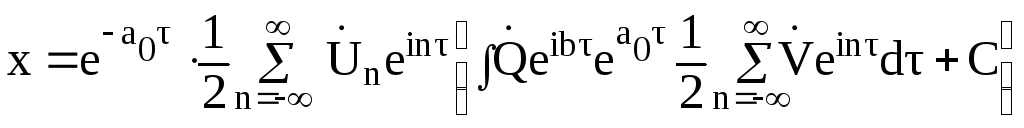, (2.42)

где свободные колебания описываются выражением:

. (2.43)

А выражение для установившегося процесса колебаний имеют вид:

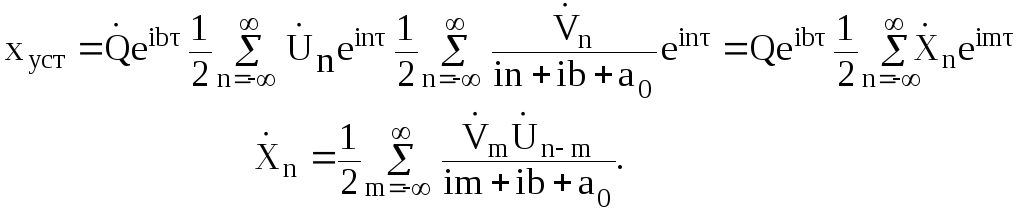(2.44)

Полученные выражения (2.32 – 2.36) и (2.43 – 2.44) позволяют исследовать процесс установления колебаний в параметрических цепях с полуцелой степенью свободы (параметрических цепях описываемых дифференциальными уравнениями первого порядка) при постоянном или гармоническом воздействиях. При любом сложном периодическом воздействии решения параметрических уравнений первого порядка с периодическим коэффициентом будут представлять собой сумму решений, полученных при рассмотрении каждого воздействия в отдельности.

Пример 2.6. Найти установившийся процесс в цепи (рис.2.8), содержащей параметрический резистор и катушку индуктивности, у которой R(t)= (1+ + snΩt), где snΩt – меандровая характеристика и соответствующее дифференциальное уравнение имеет вид :

,

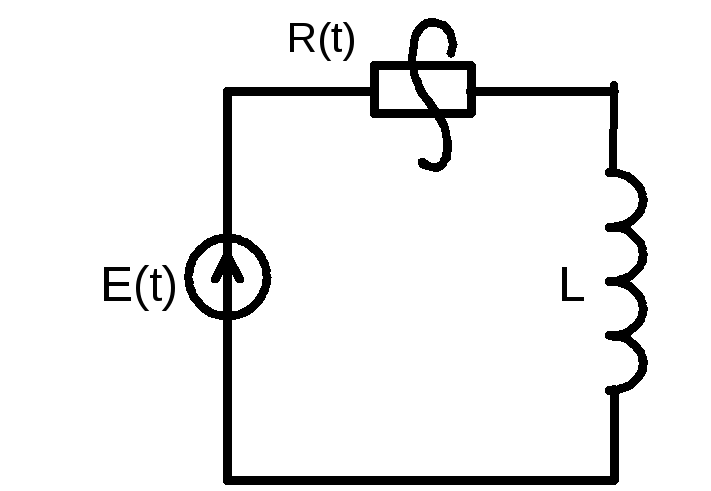
Рис.2.8. Параметрическая RL-цепь

где введено безразмерное время τ = Ωt, (Ω = ), а разложение в обобщенный ряд Фурье функцииимеет вид:

.

В соответствии с общей методикой, изложенной выше (2.39) – (2.44), нужно найти вспомогательные формулы

и .

Выполним вычисления

.

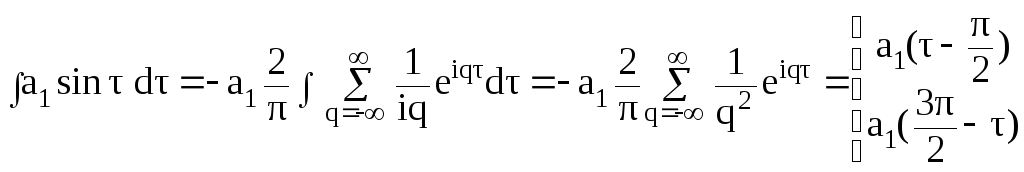
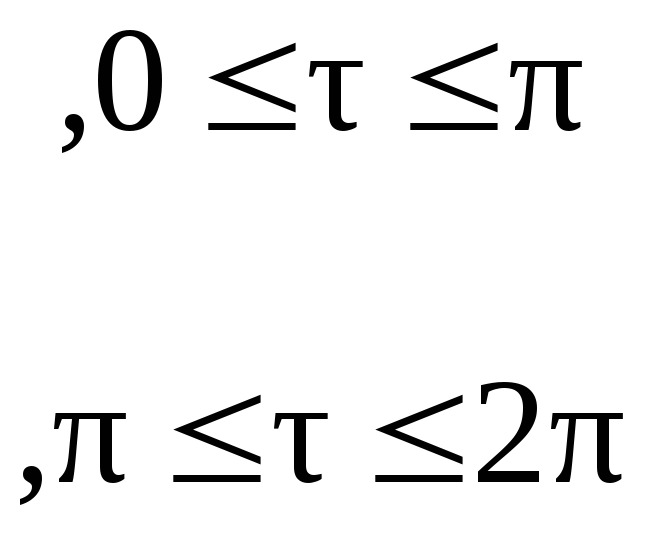
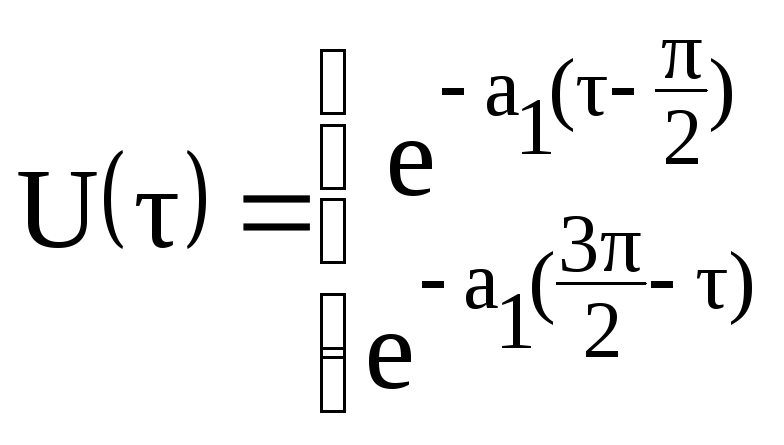
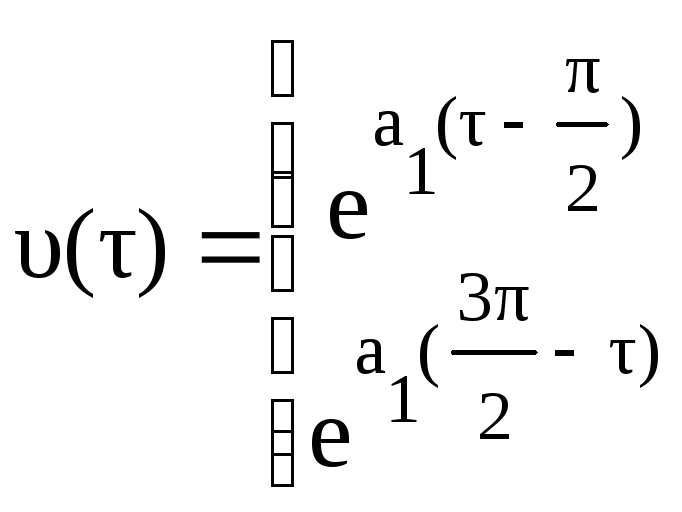
Комплексную амплитуду рядов Фурье получаем в виде

.

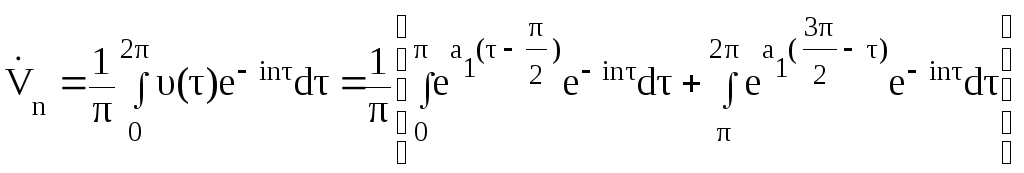Представленные интегралы вычисляются и их можно найти в любом справочнике. После несложных преобразований получаем

.

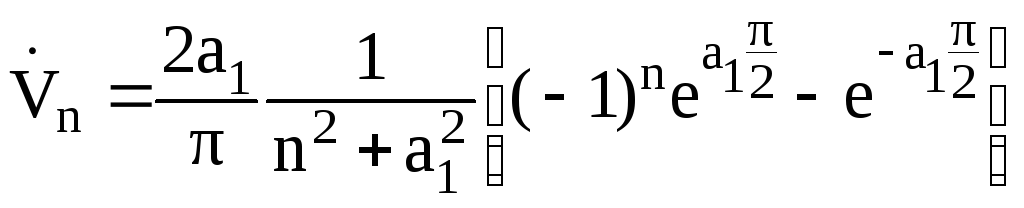Чтобы не вычислять интеграл для нахождения можно получить формулы связии

.

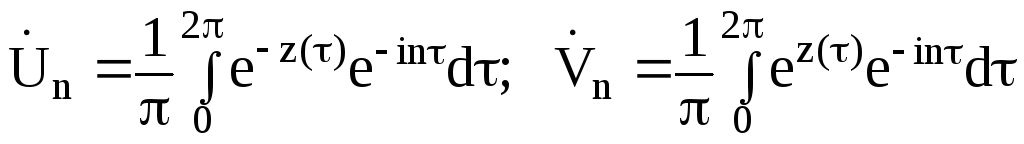В равенстве для U_n делаем замену переменных: , тогда

.

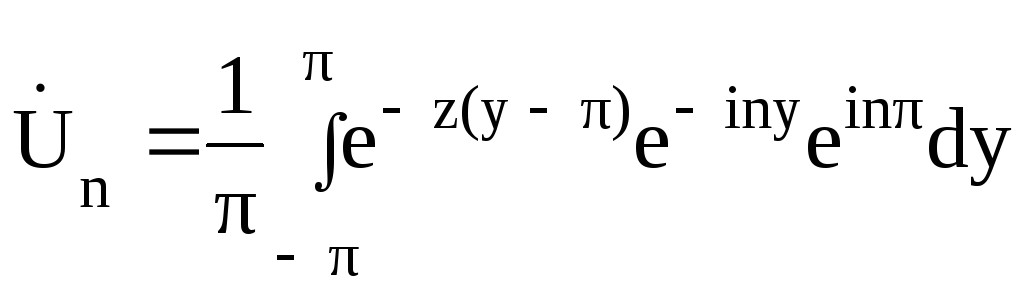Принимая во внимание свойство «нечетных рядов»: , а также то, что интеграл от периодической функции взятый по длине равной периоду не зависит от начала отсчета, получаем:

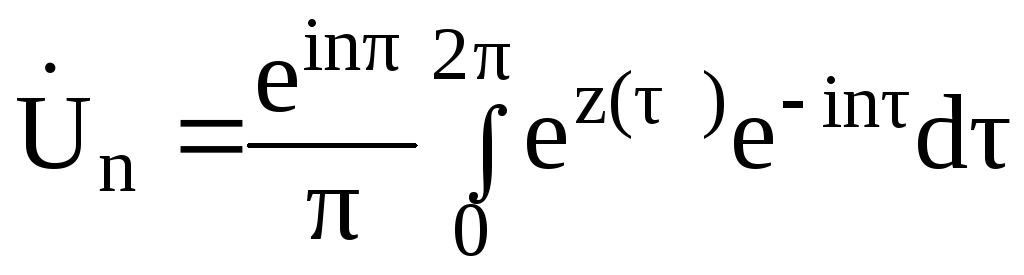, где

.

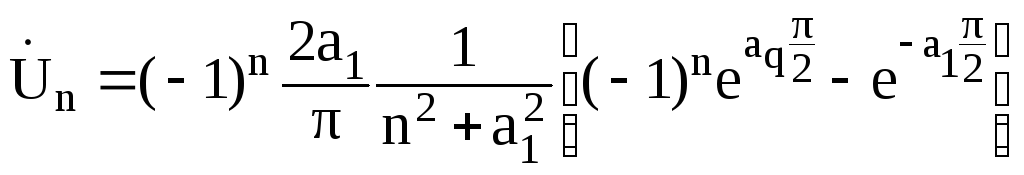Для установившегося процесса имеем следующий результат:

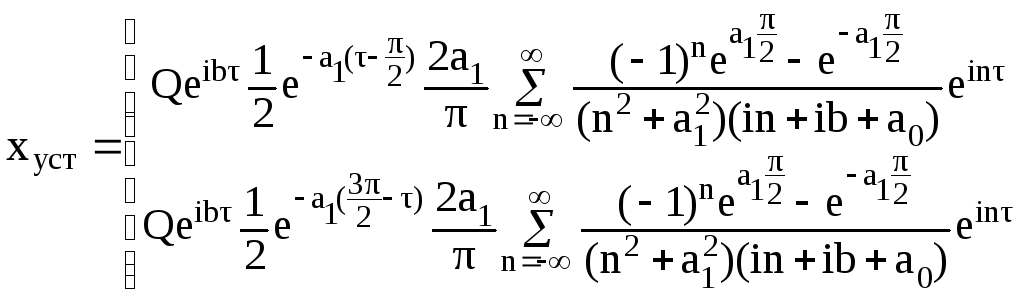
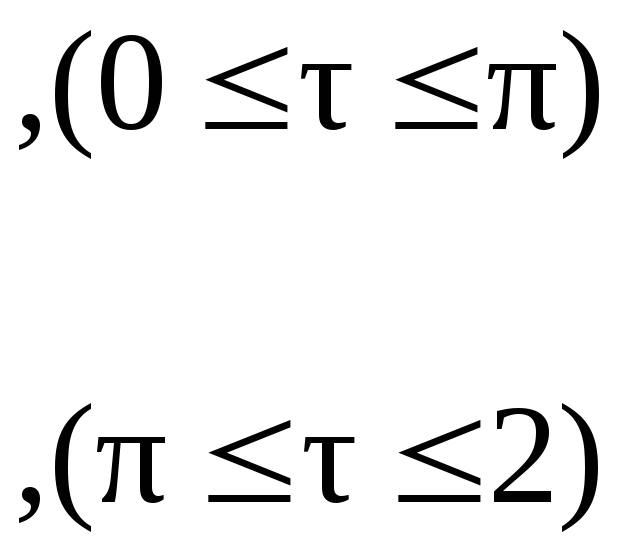. (2.44)

Суммы, входящие в последние выражения известны, поэтому путем простых преобразований получаем:

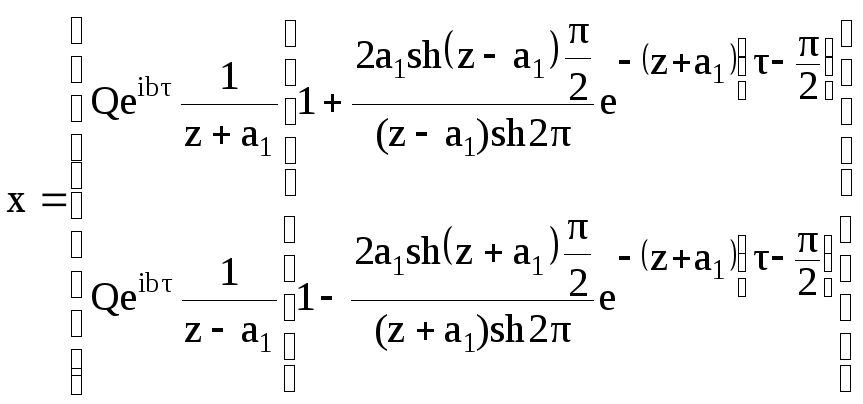
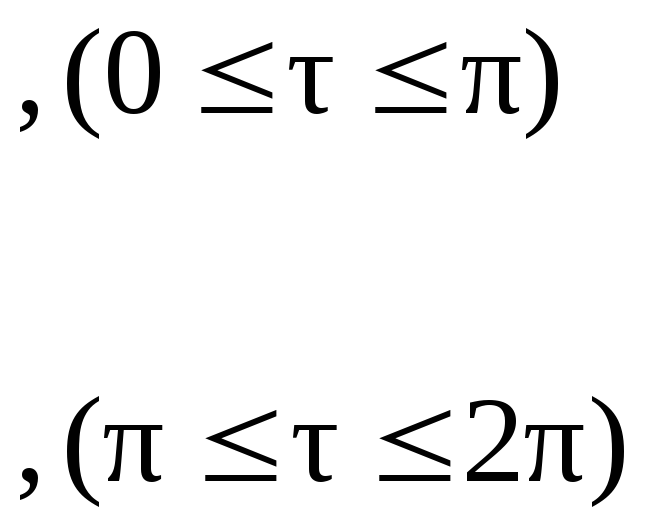, (2.45)

где .

Из выражений (2.45), как частные случаи, следуют решения целого ряда задач.

Пример 2.7. Рассмотрим параметрическую цепь (рис.2.9) в которой резистор R₂ выключается с частотой Ω. Пусть к цепи приложено постоянное напряжение Е.

Необходимо найти ток, протекающий по такой цепи. Тогда константы и переменная τ в выражении (2.45) имеют следующие значения:

.

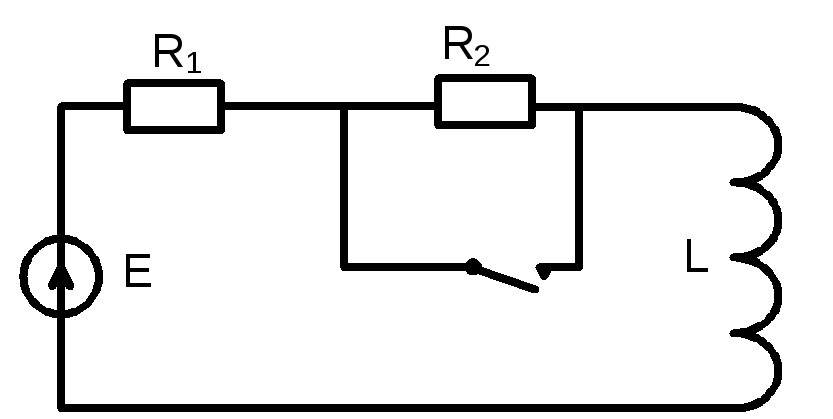
Рис.2.9. Эквивалентная схема параметрической RL–цепи

После простых преобразований выражения (2.45) примут вид

,

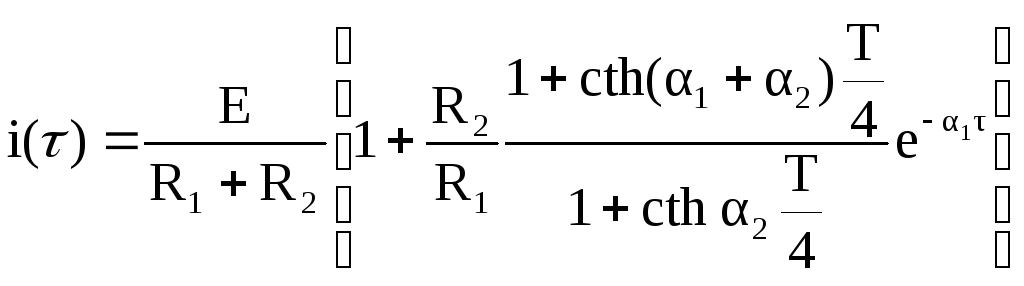
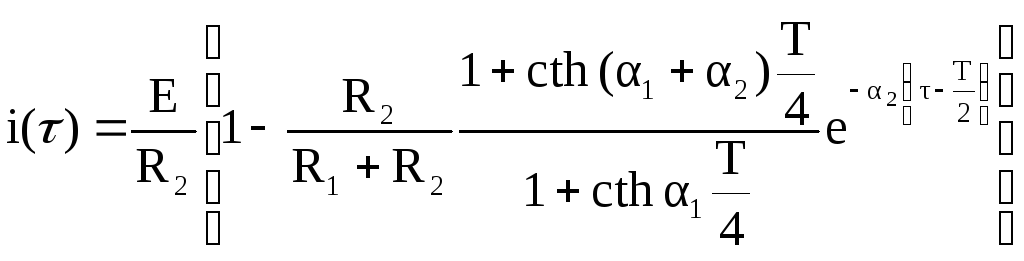
где .

Полученные выражения показывают, что в случае параметрического воздействия на цепь (рис.2.9) произошло обогащение спектра колебаний установившегося тока.