§2.3. Прохождение сигналов через параметрические r – цепи

Как было показано выше (таблица 2 и (2.18)), процессы в параметрических R – цепях описываются алгебраическими уравнениями с переменными коэффициентами и прохождение сигналов через такие цепи выражается формулой , гдеk(t) – параметрический коэффициент передачи, определяемый видом системы уравнений. В общем случае, на основании правила Крамера, коэффициент передачи можно получить в виде где- определитель системы уравнений,- соответствующее алгебраическое дополнение, А(t) – коэффициент, определяющий изменение размерности сигнала на каком-либо этапе решения задачи.

Из формулы (2.18) следует, что в самом общем случае, анализ спектрального состава отклика параметрической цепи требует использования аппарата двойных рядов Фурье. Однако в некоторых случаях удается использовать общий ряд Фурье с последующим применением тригонометрических формул.

Напомним основные формы представления функций с периодом рядами Фурье:

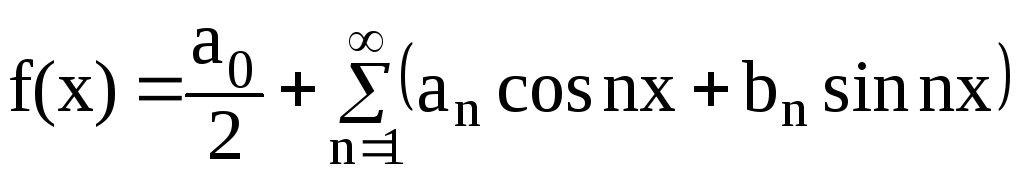, где (2.19)

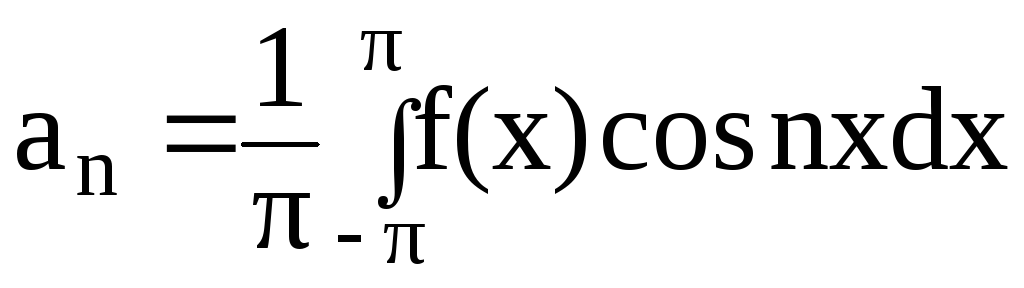; n=0;1;2…

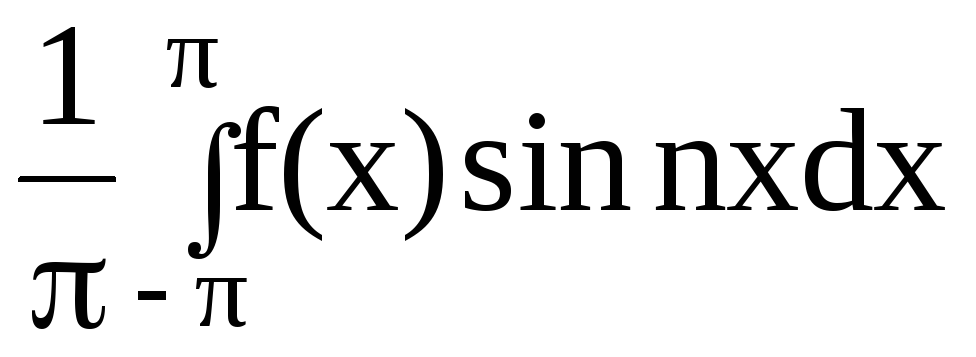; n=1;2;3… (2.20)

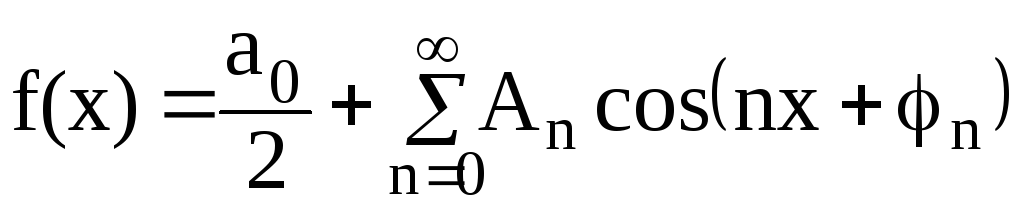, (2.21)

где ;;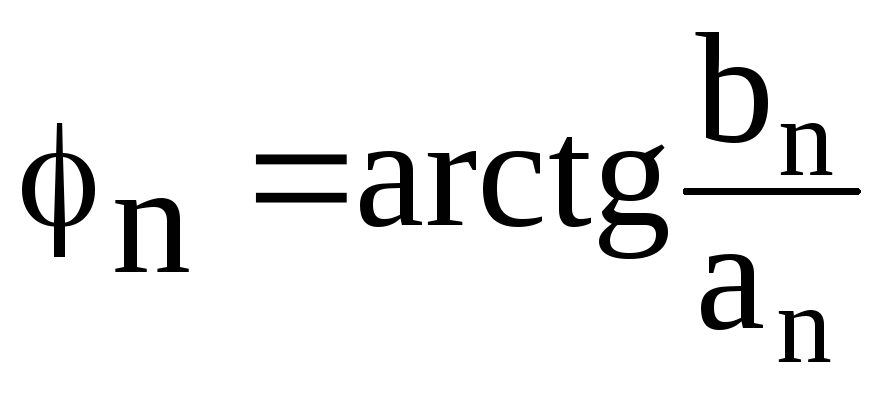 (2.22)

, (2.23)

где 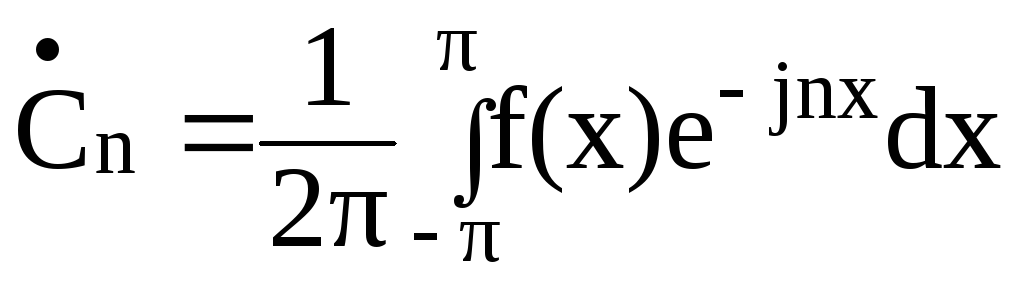. (2.24)

Проиллюстрируем анализ процессов в R – цепях примерами.

П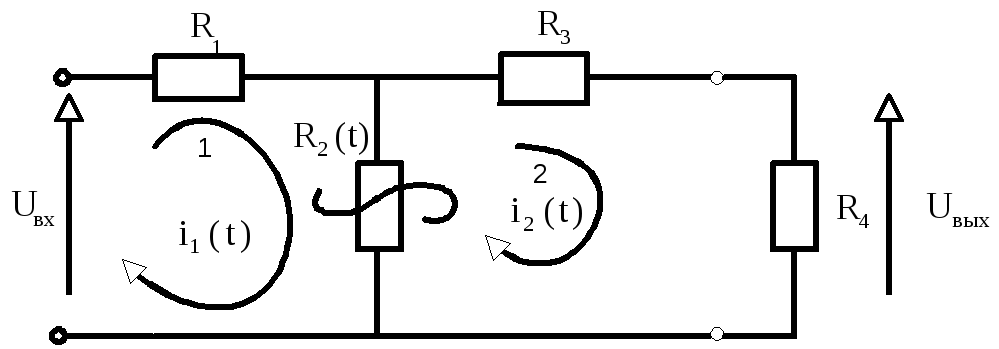ример 2.I. Определить коэффициент передачи параметрической R – цепи, представленной на рис.2.3. Используя теорему об эквивалентном генераторе, заменим входное напряжение на источник напряжения с задающей величиной равной U_вх(t). Выберем два независимых контура 1 и 2 и выберем направление обхода контуров.

Рис.2.3. Параметрическая R – цепь

Запишем систему из двух алгебраических уравнений для двух переменных контурных токов i₁(t) и i₂(t)

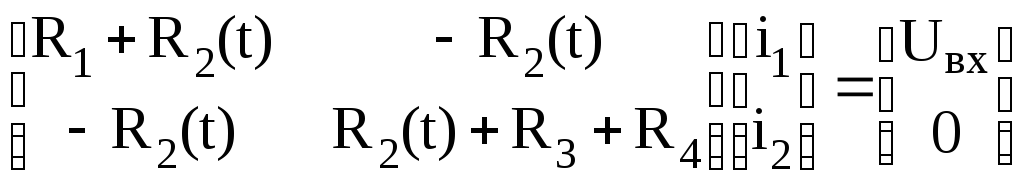
откуда находим, что

.

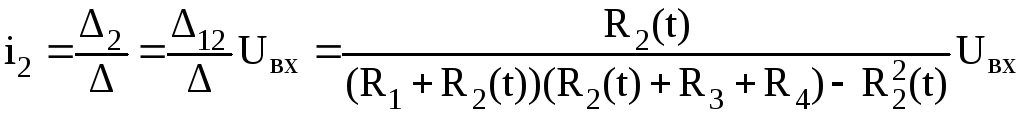Тогда

.

Выражение путем несложных преобразований можно привести к виду

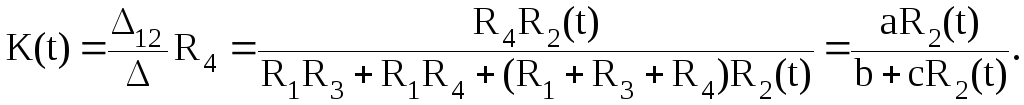Если - периодическая функция с периодом, (– круговая частота первой гармоники колебания параметра), то и его спектр определяется рядом Фурье, например, в такой форме

, где

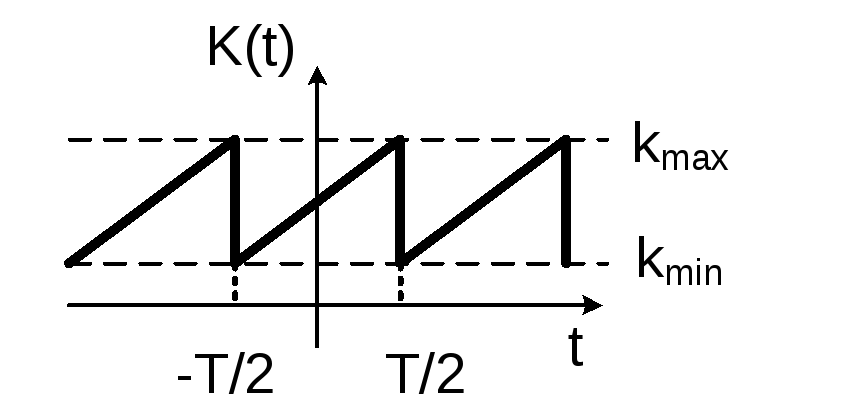Пример 2.2. Коэффициент передачи параметрической R – цепи периодически изменяется по закону, представленному графически на рис.2.4. Определить спектр К(t) в тригонометрическом базисе и построить график его амплитудной части.

Рис 2.4. Закон изменения параметра К(t)

Используя таблицу разложения функций в ряд Фурье, находим:

.

Для нечетной функции

.

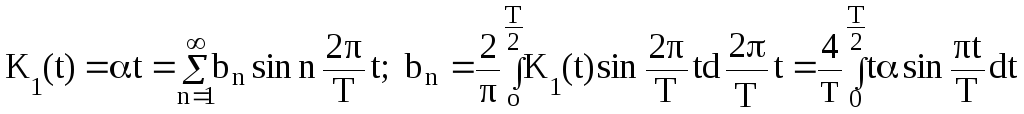Вычисляя последний интеграл, находим спектральный состав коэффициента передачи рис.2.5.:

.

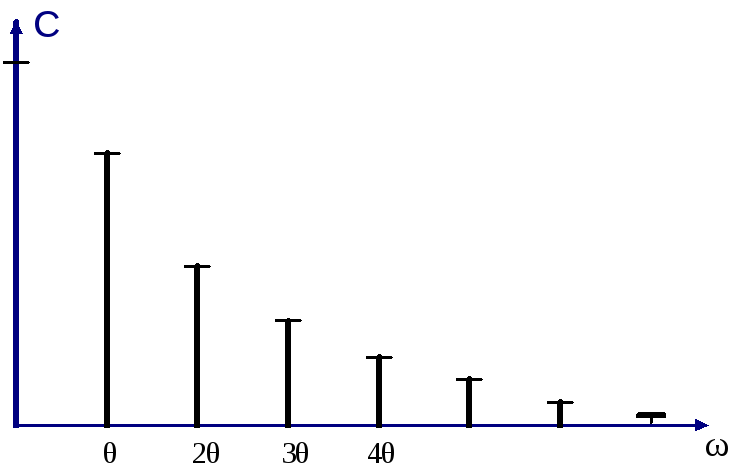
Рис.2.5. Спектральный состав параметра К(t)

Пример 2.3. Пусть к входу параметрической R – цепи с коэффициентом передачи, рассмотренном в предыдущем примере, приложено гармоническое колебание вида:

U_вх(t)=U₀cosΩt.

Тогда выходное колебание имеет следующий вид:

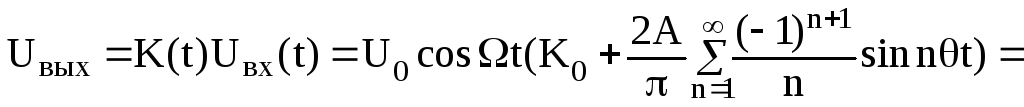
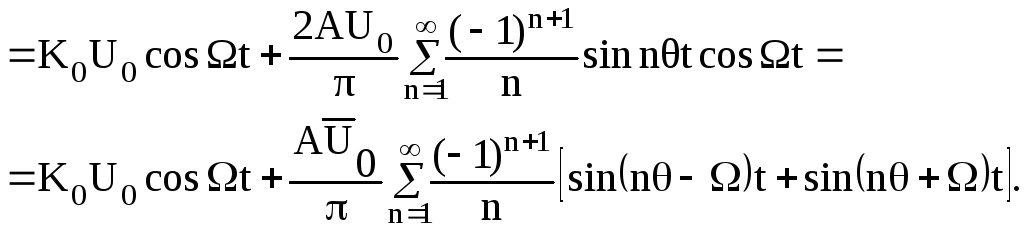
При выводе последнего соотношения использовались следующие тригонометрические соотношения:

Из полученного выражения видно, что в выходном колебании возникли гармонические составляющие, которых не было ни в колебаниях параметра, ни в колебаниях входного сигнала. Спектральный состав входного и выходного колебаний, а также спектральный состав колебаний параметра, представлен на рис.2.6.

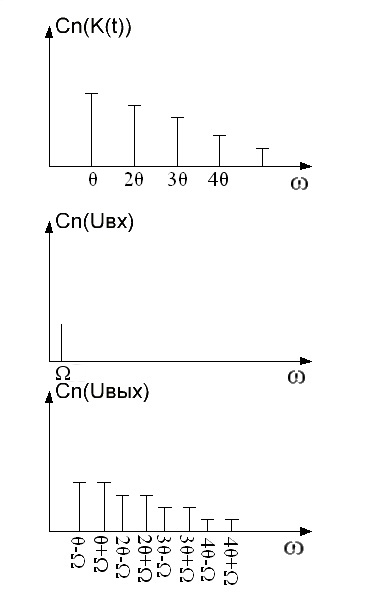
Рис.2.6. Спектральный состав входного и выходного колебаний

и колебаний параметра