Вариант №1
В урне 4 черных, 6 белых и 5 красных шаров. Наудачу извлечены 7 шаров. Найти вероятность того, что среди них окажутся 2 черных, 3 белых и 2 красных шара.
Рабочий обслуживает 3 станка. Вероятность того, что в течение смены первый станок потребует его внимания, равна 0.7, второй – 0.75, а третий – 0.85. Найти вероятность того, что в течение смены внимания рабочего потребуют: какие-либо два станка; все три станка.
Вероятности безотказной работы элементов функциональной цепи равны соответст-
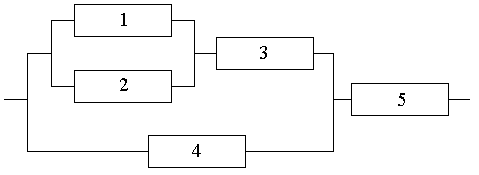
венно p1 = 0.98, p2 = 0.93, p3 = 0.85, p4 = 0.9, p5 = 0.95. Найти вероятность отказа цепи.
Три станка подают детали в общий бункер. Вероятность выпуска бракованной продукции для первого станка 0.003, для второго – 0.02 и для третьего – 0.01. Производительность первого станка в 3 раза больше производительности второго, а производительность третьего в два раза больше второго. Какова вероятность того, что взятая наудачу деталь из бункера окажется годной?
Вероятность надежной работы конструкции при приложении нагрузки равна 0.96. Найти вероятность того, что из 10 конструкций, испытанных независимо друг от друга, больше двух выйдут из строя.
Вероятность выхода из строя каждого из 900 независимо работающих элементов некоторого узла в течение 300 час. равна 0.1. Найти вероятность того, что по истечении этого времени будут работать 70 элементов; будут работать не менее 70 элементов.
Завод отправил на базу 2000 изделий. Вероятность повреждения изделия в пути равна 0.0015. Найти вероятность того, что в пути будет повреждено: хотя бы одно изделие; не более одного изделия.
В бригаде 8 рабочих, из них 5 учатся. Наудачу по списку отобраны 3 человека. Составить закон распределения дискретной случайной величины X – числа рабочих, которые учатся среди отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение σ(X) этого закона и отобразить их на многоугольнике распределения.
Дана плотность вероятностей непрерывной случайной величины X.
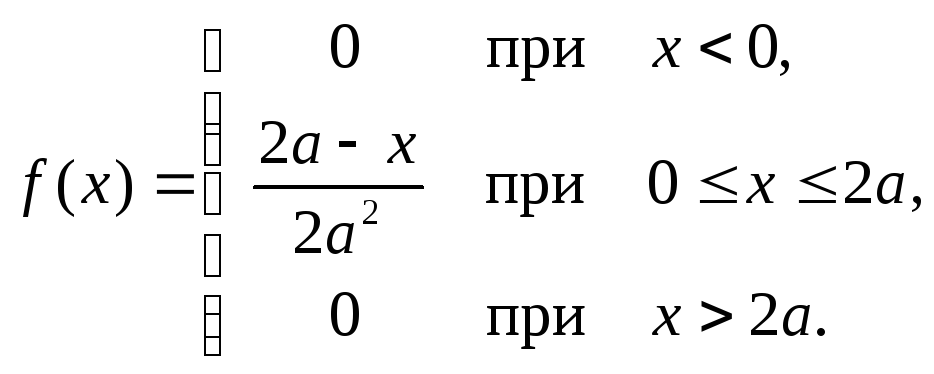
Найти параметр a, интегральную функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение σ(X) и вероятность P(a<X<1.5a). Построить графики плотности и функции распределения и показать на них математическое ожидание и среднее квадратическое отклонение σ(X).
Диаметр детали – нормально распределенная случайная величина с параметрами: a = 75 мм, σ = 2 мм. Найти вероятность того, что диаметр наудачу взятой из партии детали составит от 73.6 мм до 76.4 мм, отличается от a не более, чем на 1.4 мм. Какое отклонение диаметра от a можно гарантировать с вероятностью 0.92? В каком интервале будут заключены диаметры деталей с вероятностью 0.9973?
На основе данных о результатах определения уровня гипотимии (склонности к чувству вины) у 47-ми детей сформировать таблицу значений относительных частот для
-
№
О+ [б/р]
№
О+ [б/р]
№
О+ [б/р]
№
О+ [б/р]
№
О+ [б/р]
1
0.70
11
1.16
21
1.34
31
1.48
41
1.65
2
0.84
12
1.18
22
1.35
32
1.49
42
1.69
3
0.92
13
1.21
23
1.36
33
1.51
43
1.72
4
0.95
14
1.23
24
1.37
34
1.53
44
1.75
5
0.99
15
1.25
25
1.38
35
1.54
45
1.81
6
1.03
16
1.26
26
1.40
36
1.55
46
1.86
7
1.05
17
1.27
27
1.41
37
1.56
47
1.89
8
1.09
18
1.29
28
1.42
38
1.57
9
1.10
19
1.30
29
1.43
39
1.59
10
1.14
20
1.32
30
1.46
40
1.61
равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равных частичных интервалов.
Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0.95 и 0.99.
Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0.01, 0.05.
Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы. Для этого на ос-
-
№
X
Y
№
X
Y
№
X
Y
№
X
Y
№
X
Y
1
0.70
164
11
1.16
133
21
1.34
123
31
1.48
117
41
1.65
107
2
0.84
160
12
1.18
132
22
1.35
122
32
1.49
116
42
1.69
105
3
0.92
154
13
1.21
131
23
1.36
122
33
1.51
115
43
1.72
104
4
0.95
152
14
1.23
129
24
1.37
121
34
1.53
114
44
1.75
103
5
0.99
148
15
1.25
127
25
1.38
121
35
1.54
114
45
1.81
101
6
1.03
146
16
1.26
126
26
1.40
120
36
1.55
113
46
1.86
99
7
1.05
145
17
1.27
126
27
1.41
120
37
1.56
113
47
1.89
97
8
1.09
139
18
1.29
125
28
1.42
120
38
1.57
112
9
1.10
137
19
1.30
125
29
1.43
119
39
1.59
111
10
1.14
135
20
1.32
124
30
1.46
118
40
1.61
109
нове экспериментальных данных сформировать таблицу значений частот для равноотстоящих вариант признака X и признака Y, разбив отрезки их значений на 7 и 6 равных частичных интервалов соответственно.