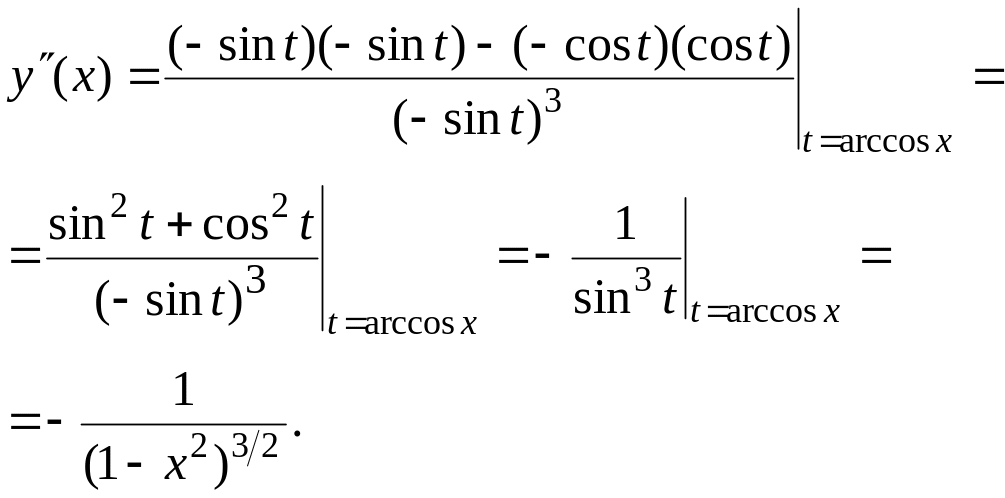- •А.П. Бырдин, н.В. Заварзин, а.А. Сидоренко, л.П. Цуканова
- •А.П. Бырдин, н.В. Заварзин, а.А. Сидоренко, л.П. Цуканова
- •1. Элементы высшей алгебры
- •1.1. Матрицы
- •1.2. Определители
- •1.3. Системы трех уравнений первой
- •Матричная запись системы линейных уравнений. Понятие обратной матрицы Рассмотрим снова систему уравнений
- •1.5. Метод гаусса
- •Векторная алгебра
- •2.1. Скалярные и векторные величины
- •Проекция
- •2.3. Линейные операции над векторами
- •3. Основные свойства линейных операций.
- •4. Теоремы о проекциях векторов.
- •Скалярное произведение векторов
- •1. Определение и основные свойства скалярного произведения.
- •2. Выражение скалярного произведения через координаты векторов.
- •Векторное произведение
- •2 . Основные свойства векторного произведения.
- •4. (Свойство сочетательности по отношению к скалярному множителю).
- •5. (Свойство распределительности относительно суммы векторов).
- •3. Выражение векторного произведения через координаты векторов.
- •Смешанное произведение трех векторов
- •В силу тождества (1) смешанное произведение можно обозначить более простым символом .
- •2. Выражение смешанного произведения через координаты векторов.
- •Аналитическая геометрия на плоскости
- •3.1. Простейшие задачи аналитической геометрии на плоскости
- •Расстояние между двумя точками.
- •Площадь треугольника.
- •3.2. Полярные координаты
- •3.3. Линии первого порядка
- •6. Общее уравнение прямой.
- •Умножая данное уравнение на μ, получаем нормальное уравнение
- •3.4. Линии второго порядка
- •1. Эллипс.
- •3. Парабола.
- •3.5. Общее уравнение линии второго порядка
- •1. Приведение общего уравнения линии второго порядка к простейшему виду.
- •Аналитическая геометрия в пространстве
- •4.1. Уравнение плоскости
- •Раскрывая скобки, приведем уравнение (1) к виду
- •4.2. Уравнение прямой
- •4.3. Поверхности второго порядка
- •5. Предел последовательности
- •5.1. Числовые последовательности
- •2. Ограниченные и неограниченные последовательности.
- •5.2. Сходящиеся последовательности
- •1. Понятие сходящейся последовательности.
- •З а м е ч а н и е. Неравенство (1) равносильно неравенствам
- •2. Основные свойства сходящихся последовательностей.
- •Нетрудно видеть, что для того, чтобы последовательность имела предел а, необходимо и достаточно, чтобы , где есть бесконечно малая.
- •5.3. Монотонные последовательности
- •1. Определение и признак сходимости монотонных последовательностей.
- •6.1. Классификация функций
- •6.2. Предел функции
- •6.3. Теоремы о пределах функции
- •6.4. Два замечательных предела
- •2. Второй замечательный предел
- •6.5 Бесконечно малые и бесконечно большие функции
- •Бесконечно малые функции.
- •2. Бесконечно большие функции.
- •6.6. Сравнение бесконечно малых
- •6.7. Неопределенные выражения
- •6.8. Непрерывные функции
- •6.9. Классификация точек разрыва
- •Определение и классификация точек разрыва функции.
- •6.10. Основные свойства непрерывных функций
- •Дифференцирование
- •7.1. Производная функции
- •4. Правая и левая производные.
- •7.2. Дифференцируемость функции
- •1. Понятие дифференцируемости функции в данной точке.
- •2. Связь между понятиями дифференцируемости и непрерывности.
- •7.3. Дифференциал функции
- •Правила дифференцирования.
- •1. Правила дифференцирования.
- •3. Производные тригонометрических функций.
- •6. Дифференцирование сложной функции.
- •7.5. Производные и дифференциалы высших порядков
- •2. Формулы для n-х производных некоторых функций.
- •4. Дифференциалы высших порядков.
- •Параметрическое задание функции
- •Применение дифференциального
- •8.1. Основные теоремы дифференциального исчисления
- •8.2. Раскрытие неопределенностей. Правило лопиталя.
- •8.3. Формула тейлора
- •Формула Тейлора.
- •3. Разложение некоторых элементарных функций по формуле Маклорена.
- •8.4. Исследование поведения функций
- •1. Признак монотонности функции.
- •2. Отыскание точек локального экстремума функции.
- •Ответы к п.П. 2.1 2.4
- •Задачи к п. 2.5
- •Ответы к п. 2.5
- •Задачи к п. 2.6
- •Ответы к п. 2.6.
- •Задачи к п.П. 3.1 – 3.3
- •Ответы к п.П. 3.1 – 3.3
- •Задачи к п.П. 3.4 – 3.5
- •Ответы к п.П. 3.4 – 3.5
- •Задачи к п.П. 4.1 4.2
- •Задачи к п. 4.3
- •Ответы к п. 4.3
- •Задачи к п.П. 5.1 6.4
- •Ответы к п.П. 5.1 6.4
- •Задачи к п.П. 6.5 6.9
- •Ответы к п.П. 6.5 6.9
- •Задачи к п.П. 7.1 – 7.6
- •Ответы к п.П. 7.1 – 7.6
- •Задачи к п.П. 8.1 – 8.3
- •Ответы к п.П. 8.1 – 8.3
- •Задачи к п. 8.4
- •Ответы к п. 8.4
- •Вопросы к экзамену
- •Рекомендуемая литература
- •Оглавление
- •7. Дифференцирование ……..…………………………..125
- •8. Применение дифференциального исчисления к исследованию функций………...……………………….…..150
- •394026 Воронеж, Московский просп., 14
Параметрическое задание функции
И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ
Параметрическое задание функции. Пусть даны две функции
х = (t), y = (t) (1)
одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если x = (t) строго монотонна, то обратная к ней функция t = (х) однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной х посредством переменной t, называемой параметром: у = (Ф(х)).
В этом случае говорят, что функция у от х задана параметрически с помощью уравнений (1).
Отметим, что функция (ф(х)) непрерывна в силу теоремы о непрерывности сложной функции.
Пример 1. Пусть x = R cos t, y = R sin t ( 0 t ). Так как функция x=R cos t убывает при 0 t , то данные уравнения задают параметрически функцию у от х. Если выразить t через х из первого уравнения и подставить во второе, то получим искомую функцию переменной х в явном виде.
Это еще легче сделать, если заметить, что х2 + у2 = R2 (cos2 t + sin2 t) = R2.
Отсюда у
=
![]() или у =
или у =
![]() Так как функция у
= R
sin
t
неотрицательна для
0
t
,
то перед радикалом выбираем знак плюс:
у=
Так как функция у
= R
sin
t
неотрицательна для
0
t
,
то перед радикалом выбираем знак плюс:
у=
![]() .
Если
t
2
, то у
=
.
Если
t
2
, то у
=
Таким образом, можно сделать вывод, что когда t изменяется от 0 до 2, то формулы x = R cos t и y = R sin t определяют две функции переменной х, графики которых образуют окружность радиуса R.
Пример 2. Пусть х = а cos t, у = b sin t (0 t 2).
Данные равенства являются параметрическими уравнениями эллипса, так как эллипс получается из окружности радиуса а сжатием ее в а/b раз вдоль оси Оу. Из примера 1 следует, что параметрическими уравнениями окружности x2 + y2 = a2 являются уравнения x = a cos t, y = a sin t ( 0 t 2). Итак, параметрические уравнения эллипса получаются из параметрических уравнений окружности умножением правой части уравнения для ординаты у на b/а и имеют вид: x = a cos t, у = b sin t (0 t 2). Можно поступить проще. Исключая из этих уравнений параметр t (разрешая их относительно cos t и sin t, возводя полученные равенства в квадрат и складывая), получаем
(x/a)2 + (y/b)2 = cos2 t + sin2 t = 1 или х2/а2 + у2/b2 = 1 уравнение эллипса. Параметрическое задание функции имеет особо важное значение при изучении движения точки. Если точка движется на плоскости, то ее координаты х, у являются функциями времени t. Задав эти функции х = (t), у = (t), мы полностью определим движение точки. Для каждого промежутка времени, в котором функция (t) строго монотонна, можно, как и раньше, определить функцию у = (Ф(х)), графиком которой является кривая, описываемая за этот промежуток времени движущейся точкой. В последнем примере функции описывали движение точки по эллипсу.
2. Дифференцирование функции, заданной параметрически. Предположим теперь, что функции х = (t) и y= (t) имеют производные, причем (t) 0 на некотором промежутке. Тогда производная функции, заданной параметрически, выражается формулой
![]() (2)
(2)
Пример 1. Найти у'(х), если x = R cos t, y = R sin t ( 0 t ).
Р е ш е н и е. Т. к. в нашем случае t = Ф(х) = arccos (x/R) ), то по формуле (2) получаем
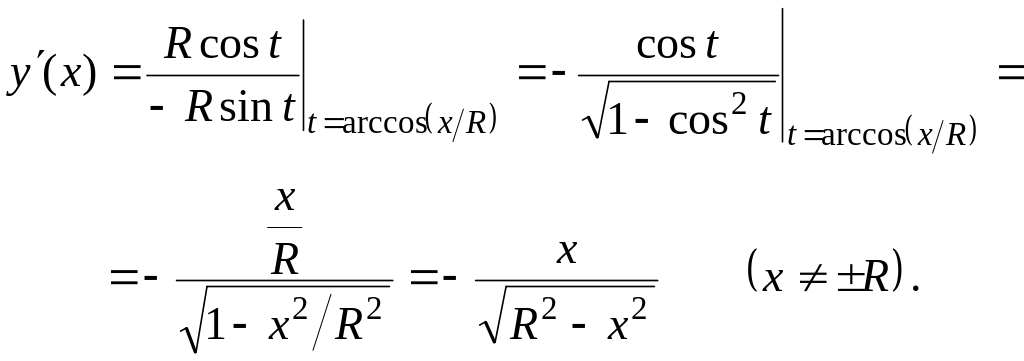
Пусть существуют
вторые производные функций
![]() и
и
![]() в
некоторой точке
t.
Тогда можно вычислить вторую производную
функции, заданной параметрически.
Заметим, что функция
в
некоторой точке
t.
Тогда можно вычислить вторую производную
функции, заданной параметрически.
Заметим, что функция
![]() ,
в свою очередь, задана параметрически
уравнениями
,
в свою очередь, задана параметрически
уравнениями
![]() и
х = (t).
Следовательно,
и
х = (t).
Следовательно,
![]() (3)
(3)
Аналогично можно получить производную от у по x любого порядка.
Пример 2. Найти у(х), если x = cos t, y = sin t ( 0 t ).
Р е ш е н и е. y(t) = cos t, у"(t)= sin t; x'(t) = sin t, х" (t) = cos t, поэтому по формуле (3) найдем