7. Применение дифференциального

ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ

8.1. Основные теоремы дифференциального исчисления

Теорема 1 (теорема Ферма). Пусть функция определена на интервале (a,b) и в некоторой точке этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке существует производная, то она равна нулю, т. е.

Геометрический смысл теоремы Ферма состоит в том, что если в точке дифференцируемая функция имеет наибольшее или наименьшее значение, то в точке касательная к графику функции параллельна оси Ox (рис.49).

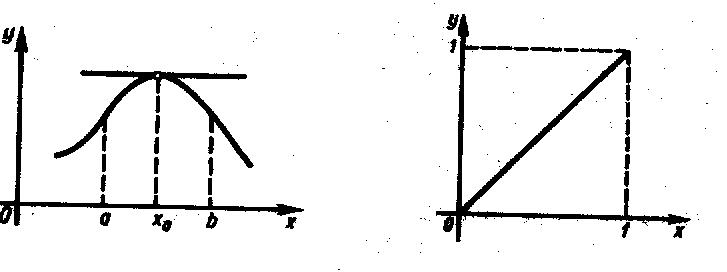
Рис. 49 Рис. 50

З а м е ч а н и е. Теорема неверна, если функцию рассматривать на отрезке [a,b]. Так функция = x на отрезке [0,1] в точке x = 0 принимает наименьшее, а в точке x = 1 – наибольшее значение, однако как в той, так и в другой точке производная в нуль не обращается, а равна единице (рис. 50).

Теорема 2 (теорема Ролля). Пусть на [a,b] определена функция , причём: 1) непрерывна на [a, b]; 2) дифференцируема на (a,b); 3) f(a) = f(b). Тогда существует точка , в которой f(с)=0.

Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [a,b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах равные значения, существует точка (с; f(с)), в которой касательная параллельна оси Ох (рис. 3). На рис. 51 в точке с функция принимает наибольшее значение.

Следует отметить, что все три условия теоремы Ролля существенны. Чтобы убедиться в этом, достаточно привести примеры функций, для которых выполнялись бы два условия теоремы, а третье не выполнялось и производные которых не

Рис. 51

Рис. 3

обращались бы в нуль ни в одной точке. Так, например, функция f(x)=x, x[0,1] (см. рис. 2) удовлетворяет условиям 1 и 2, но не удовлетворяет условию 3 и для неё не существует точки с такой, что f(с)=0. Рассмотрим ещё два примера. Функция f(x), равная x, если , и равная 0, если x=1 (рис. 52), удовлетворяет условиям 2 и 3, но не удовлетворяет условию 1. Функция , x[1,1] (рис. 53) удовлетворяет условиям 1 и 3, но не удовлетворяет условию 2. Для этих функций также не существует точки, в которой их производная обращалась бы в нуль.

Рис. 52 Рис. 53

Отметим, что в математике существенность тех или иных условий доказываемых теорем проверяется построением соответствующих примеров, когда невыполнение того или иного условия теоремы приводит к тому, что утверждение теоремы становится неверным.

Теорема 3 (теорема Лагранжа). Пусть на [a,b] определена функция f(x), причём: 1) f(x) непрерывна на [a,b]; 2) f(x) дифференцируема на (a,b). Тогда сущест-вует точка такая, что справедлива формула

Установим геометрический смысл теоремы Лагранжа (рис.54). Величина является угловым коэффициентом секущей, проходящей через точки и графика функции а  угловой коэффициент касательной к графику в точке Из теоремы Лагранжа следует, что существует точка с такая, что касательная к графику в точке параллельна секущей Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.

З а м е ч а н и е 1. Равенство

Рис. 74

(1)

называется формулой Лагранжа или формулой конечных приращений.

З а м е ч а н и е 2. Так как точка с лежит между a и b, то , где . Учитывая это, формулу Лагранжа можно записать в виде

З а м е ч а н и е 3. Если поло-жить то получим Такая запись формулы Лагранжа часто бывает удобнее, чем запись в виде (1).

Как будет показано в дальнейшем, теорема Лагранжа лежит в основе доказательства многих формул и теорем анализа.

Теорема 4 (теорема Коши). Пусть функции f(x) и g(x) непрерывны на [a,b] и дифференцируемы на (a,b). Пусть, кроме того, . Тогда существует точка такая, что справедлива формула

. (2)

З а м е ч а н и е. Формула (2) называется формулой Коши или обобщенной формулой конечных приращений.