1.3. Системы трех уравнений первой

СТЕПЕНИ С ТРЕМЯ НЕИЗВЕСТНЫМИ

Теория матриц и определителей имеет широкое применение как в самой математике, так и в ее приложениях. Это очень удобный и часто используемый в самых разнообразных исследованиях математический аппарат.

Рассмотрим применение матриц и определителей к исследованию системы трех уравнений первой степени с тремя неизвестными x, y, z:

(1)

(коэффициенты а₁ , a₂ , a₃ , b₁ , b₂ , b₃ , c₁ , c₂ , c₃ и свободные члены h₁ , h₂ , h₃ считаются заданными).

Тройка чисел называется решением системы (1), если в результате подстановки этих чисел вместо x, y, z все три уравнения (1) обращаются в тождества.

В дальнейшем основную роль будут играть следующие четыре определителя:

, ,

, .

Определитель  называется главным определителем системы (1). Определители , , получаются из определителя системы  заменой свободными членами элементов соответственно первого, второго и третьего столбцов.

Теорема (правило Крамера). Если главный определитель  системы (1) отличен от нуля, то существует, и притом единственное, решение этой системы, и оно выражается формулами Крамера

(2)

Пример. Решить систему уравнений

Решение. Так как то данная система имеет единственное решение, определяемое формулами (2):

З а м е ч а н и е 1. Если главный определитель системы (1) равен нулю, а хотя бы один из вспомогательных определителей отличен от нуля, то система (1) не имеет решения.

З а м е ч а н и е 2. Если главный определитель системы (1) и все вспомогательные определители равны нулю, то система (1) либо не имеет решения, либо имеет бесконечное множество решений.

Если , то система (1) называется однородной.

З а м е ч а н и е 3. Однородная система всегда имеет нулевое решение , единственным это решение будет только тогда, когда главный определитель системы отличен от нуля.

4. Матричная запись системы линейных уравнений. Понятие обратной матрицы Рассмотрим снова систему уравнений

(1)

Введем следующие обозначения:

(2)

Тогда, используя правило умножения матриц, систему (1) можно записать в эквивалентном матричном виде

AX = Н, (3)

где А – заданная матрица, Н – заданный вектор-столбец, Х – неизвестный вектор-столбец. Решением уравнения (3) является такой вектор-столбец Х, который обращает уравнение (3) в тождество.

Пусть определитель  матрицы А отличен от нуля. Тогда, как установлено в п. 1.3, система (1) и, следовательно, система (3) имеют единственное решение, которое находится по формулам Крамера. Дадим теперь другую форму записи решения уравнения (3). Для этого введем понятие обратной матрицы.

Определение. Обратной для матрицы А называется такая матрица (обозначение А^-1), которая удовлетворяет условиям

А^-1  А = А  А^-1 = Е, (4)

где Е – единичная матрица.

Если определитель   0, то обратной для матрицы А является матрица:

(5)

где, как и ранее, A_i , B_i , C_i – алгебраические дополнения соответственно элементов а_i , b_i , c_i (i = 1, 2, 3).

Таким образом, обратной для матрицы А является матрица А^-1, определяемая формулой (5). Из равенства (4) следует, что матрица А – обратная для матрицы А^-1. Поэтому матрицы А и А^-1 называются взаимнообратными.

З а м е ч а н и е. Если определитель матрицы А равен нулю ( = 0), то обратная матрица не существует.

Воспользуемся обратной матрицей для решения уравнения (3). Умножая уравнение (3) слева на матрицу А^-1, получаем

(6)

Так как А^-1 А = Е, а ЕХ = Х, то из (6) следует равенство

Х = А^-1Н. (7)

Итак, если   0, то решение уравнения (3), а значит и системы (1), можно записать в матричном виде (7). Это решение, конечно, то же самое, что было получено в п. 1.3 по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1) при   0, можно непосредственно проверить, если подставить в формулу (7) выражение (5) для А^-1 и выражения (2) для Х и Н.

Имеем откуда

т. е. получили формулы Крамера.

Пример. Решить систему уравнений

Р е ш е н и е. Имеем

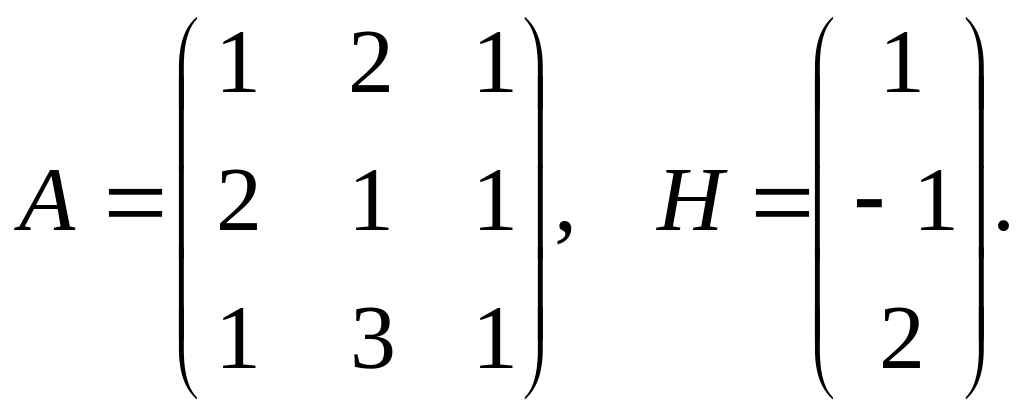
Определитель матрицы А равен 1  0. Следовательно, матрица А имеет обратную. По формуле (5) находим

Используя матрицу А^-1, по формуле (7) получаем

откуда