3. Парабола.

Определение 7. Параболой называется множество всех точек, плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Для вывода уравнения параболы введем на плоскости прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус перпендикулярно директрисе, и будем считать ее положительным направлением направление от директрисы к фокусу; начало координат расположим посередине между фокусом и ди­ректрисой. Выведем уравнение параболы в выбранной системе ко­ординат.

Пусть М (х; у)  произвольная точка плоскости. Обозначим через r расстояние от точки М до фокуса F (r = |MF|), через d  расстояние от точки М до директрисы, а через р  расстояние от фокуса до директрисы (рис. 27). Величину р называют парамет­ром параболы, его геометрический смысл будет раскрыт далее. Точка М лежит на данной параболе в том и только в том случае, когда r = d. Преобразовав полученное равенство, получим

у² = 2рх. (4)

Уравнению (4) удовлетворяют координаты точек данной параболы и только они, т. е. уравнение (4) является уравнение данной параболы и оно называется каноническим уравнением параболы. Это уравнение второй степени. Таким образом, парабола есть линия второго порядка.

Исследуем теперь форму параболы по ее уравнению (4). Так как уравнение (4) содержит у только в четной степени, то парабола симметрична относительно оси Ох. Следовательно, достаточно рассмотреть только ее часть, лежащую в верхней полуплоскости. Для этой части у  0, поэтому разрешая уравнение (4) относительно у, получаем

. (5)

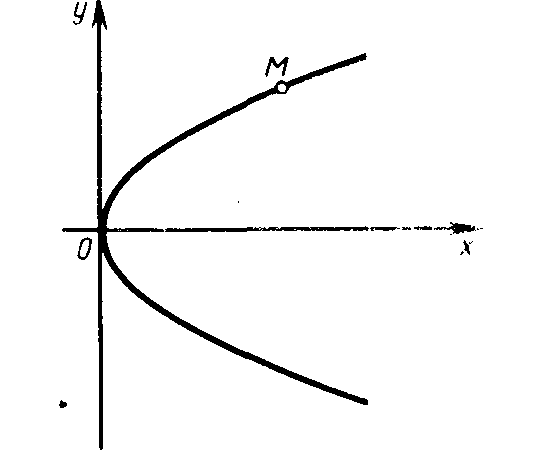
Рис. 27 Рис. 28

Из равенства (5) вытекают следующие утверждения.

1. Если х < 0, то уравнение (5) дает мнимые значения

у. Следовательно, левее оси Оу ни одной точки параболы нет. 2) Если х = 0, то у = 0. Таким образом, начало координат лежит на параболе и является самой «левой» ее точкой.

3) При возрастании х возрастает и у, причем если то и

Таким образом, переменная точка М (х;у), перемещается по параболе с ростом х, исходит из начала координат и движется «вправо» и «вверх», причем при удаление точки М как от оси Оу, так и от оси Ох является бесконечным.

Производя симметричное отражение рассмотренной части параболы относительно оси Ох, получим всю параболу (рис. 28), заданную уравнением (5).

Точка О называется вершиной параболы, ось симметрии (ось Оx)  осью параболы. Число р, т. е. параметр параболы, выражает расстояние от фокуса до директрисы. Выясним, как влияет параметр параболы на ее форму. Для этого возьмем какое-нибудь определенное значение абсциссы, например х = 1, и найдем из уравнения (5) соответствующие значения ординаты: у =  . Полу­чаем на параболе две точки и , симметричные относительно ее оси; расстояние между ними равно 2 . Отсюда заключаем, что это расстояние тем больше, чем больше р. Следовательно, параметр р характеризует «ширину» области, ограниченной параболой. В этом и состоит геометриче­ский смысл параметра р.

П

арабола, уравнение которой , расположена

а) б)

Рис. 29 в)

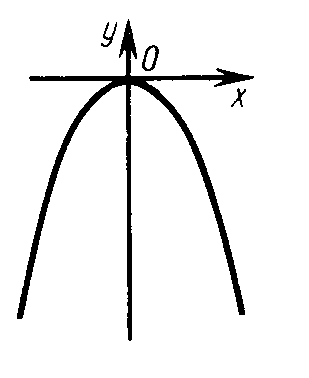
слева от оси ординат (рис. 29, а). Вершина этой параболы совпадает с началом координат, осью симметрии является ось Ох.

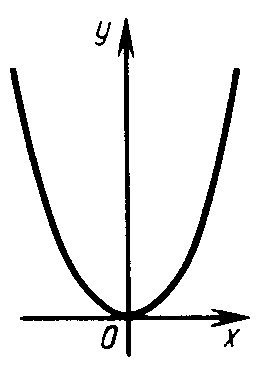
Уравнение , является уравнением параболы, вершина которой совпадает с началом координат, а осью симметрии является ось Оу (рис. 29, б). Эта парабола лежит выше оси абсцисс. Уравнение , определяет параболу, лежа­щую ниже оси Ох, с вершиной в начале координат (рис. 29, в).