5.2. Сходящиеся последовательности

1. Понятие сходящейся последовательности.

Определение. Число а называется пределом последовательности , если для любого положительного числа ε существует номер N такой, что при n > N выполняется неравенство

 ε. (1)

С помощью логических символов это определение можно записать в виде

Последовательность, имеющая предел, называется сходящейся. Последовательность, не являющаяся сходящейся, называется расходящейся.

Если последовательность сходится и имеет своим пределом число а, то символически это записывается так:

(2)

Пример. Используя определение предела последовательности, докажем, что

Возьмем любое число ε  0. Так как то для нахождения значений n, удовлетворяющих неравенству  ε, достаточно решить неравенство  ε, откуда получаем n  (1–ε)/ε. Следовательно, в качестве N можно взять целую часть числа (1–ε)/ε , т.е. Тогда неравенство  ε будет выполняться при всех n  N. Этим и доказано, что

З а м е ч а н и е. Неравенство (1) равносильно неравенствам

ε  х_n – а  ε или а – ε  х_n  a + ε,

которые означают, что элемент х_n находится в ε-окрестности точки а, точнее, существует номер N такой, что все элементы х_n с номерами n  N находятся в этой ε-окрестности.

2. Основные свойства сходящихся последовательностей.

Теорема 1. Сходящаяся последовательность имеет только один предел.

Теорема 2. Сходящаяся последовательность ограничена.

З а м е ч а н и е. Ограниченная последовательность может и не быть сходящейся.

Теорема 3. Сумма (разность) двух сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей и .

Теорема 4. Произведение двух сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей и .

Теорема 5. Частное двух сходящихся последовательностей и при условии, что предел отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и .

Пример. Найти

Р е ш е н и е. При числитель и знаменатель дроби стремятся к бесконечности, следовательно, применить теорему о пределе частного нельзя, так как в условии этой теоремы предполагается существование конечных пределов. Поэтому сначала преобразуем данную последовательность, разделив числитель и знаменатель на . Затем, применяя теоремы о пределе частного и о пределе суммы, найдем

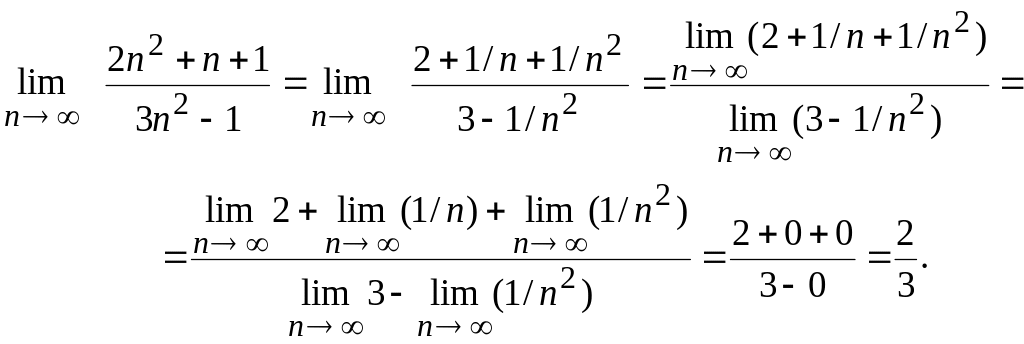
Теорема 6 (предельный переход в неравенствах). Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству то и предел а этой последовательности удовлетворяет неравенству

С л е д с т в и е. Если элементы сходящихся последовательностей и , начиная с некоторого номера, удовлетворяют неравенству то их пределы удовлетворяют неравенству

З а м е ч а н и е. Из строгого неравенства вообще говоря, не вытекает строгое же неравенство а только, по-прежнему, вытекает нестрогое

Теорема 7 (предел промежуточной переменной). Пусть даны три последовательности , и , причем для всех n, и пусть последовательности и имеют один и тот же предел а. Тогда последовательность также имеет предел а.

3. Бесконечно малые и бесконечно большие последовательности.

Определение 1. Последовательность , имеющая предел, равный нулю, называется бесконечно малой.