2. Проекция

1. Проекция вектора на ось. Пусть в пространстве заданы ось и и некоторый вектор . Проведем через точки А и В плоскости, перпендикулярные оси и. Обозначим через А' и В' точки пересечения этих плоскостей с осью (рис. 3).

Определение. Проекцией вектора на ось и называется величина А'В' направленного отрезка на оси и. Напомним, что А'В' = , если совпадает с направлением оси и, А'В' =  , если направление противоположно направлению оси и.

Обозначается проекция вектора на ось и так: пр_и .

Теорема 1. Проекция вектора на ось и равна длине вектора , умноженной на косинус угла между вектором и осью и, т. е.

пр_и = ,

где   угол между вектором и осью и .

З а м е ч а н и е 1. Равные векторы имеют равные проекции на одну и ту же ось.

2. Проекции вектора на оси координат. Пусть в пространстве заданы прямоугольная система координат Oxyz и произвольный вектор . Пусть, далее, X = пр_x , Y = пр_y , Z = пр_z . Проекции X, Y, Z вектора на оси координат называют его координатами.. При этом пишут =

Теорема 2. Каковы бы ни были две точки , координаты вектора определяются следующими формулами: X = x₂  x₁, Y = y₂  y₁ , Z = z₂  z₁ .

З а м е ч а н и е 2. Если вектор выходит из начала координат, то координаты вектора равны координатам точки B.

3. Направляющие косинусы вектора. Пусть дан произвольный вектор будем считать, что выходит из начала координат О и не лежит ни в одной координатной плоскости. Проведем через точку А плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок ОА (рис. 4). Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его измерений. Следовательно,

(1)

Формула (1) выражает длину произвольного вектора через его координаты.

Рис. 4

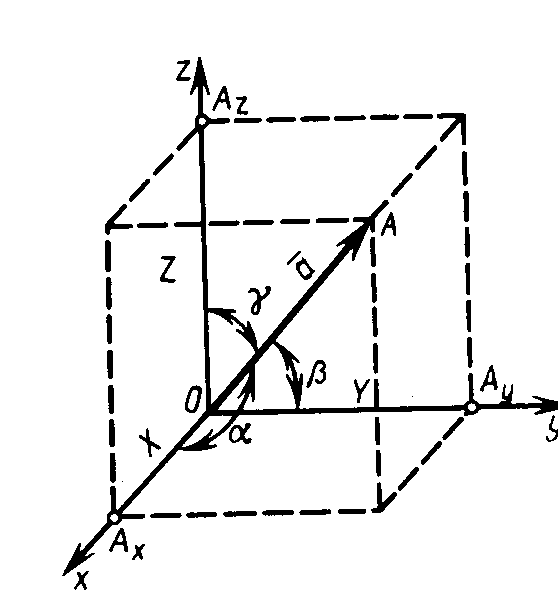
Обозначим через , ,  углы между вектором и осями координат. Очевидно,

Числа cos , cos , cos  называются направляющими косинусами вектора . Возводя в квадрат левую и правую части каждого из этих равенств и суммируя полученные результаты, имеем cos²  + cos²  + cos²  = 1, т. е. сумма квадратов направляющих косинусов любого вектора равна единице.

В заключение пункта рассмотрим задачу. Пусть даны две произвольные точки . Найдем расстояние d между ними. Используя теорему 2 и формулу (1), сразу получаем искомый результат а так как d – длина вектора , то

2.3. Линейные операции над векторами

И ИХ ОСНОВНЫЕ СВОЙСТВА

Линейными операциями над векторами называются операции сложения, вычитания векторов и умножения векторов на числа.

1. Сложение двух векторов. Пусть даны два вектора . Суммой называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора ( рис. 5, а ).

З а м е ч а н и е 1. Действие вычитания векторов обратно действию сложения, т. е. разностью векторов называется вектор, который в сумме с вектором дает вектор ( рис. 5, б ).

З а м е ч а н и е 2. Определив сумму двух векторов, можно найти сумму любого числа данных векторов. Пусть, например, даны три вектора Сложив и , получим вектор . Прибавив к нему теперь вектор , получим вектор .

2. Произведение вектора на число. Пусть даны вектор и число . Произведением называется вектор, который коллинеарен вектору , имеет длину, равную , и направление такое же, как и вектор , если   0, и противоположное, если   0 (рис. 6).

Геометрический смысл операции умножения вектора на число можно выразить следующим образом : если  1, то при умножении вектора на число  вектор ”растягивается” в  раз, а если  1 – “сжимается” в 1/ раз. При   0 вектор изменяет направление на противоположное. На рис. 6 изображен случай  1.

Если  = 0 или , то произведение считается равным нулевому вектору.

 (  0)

 (  0)

а) б)

Рис. 5 Рис. 6

З а м е ч а н и е 3. Используя определение умножения вектора на число, нетрудно доказать, что если векторы и коллинеарны и , то существует (и притом только одно) число  такое, что .