Умножая данное уравнение на μ, получаем нормальное уравнение

.

По формуле (8) находим искомое расстояние:

.

3.4. Линии второго порядка

Рассмотрим три вида линий: эллипс, гиперболу и параболу, уравнения которых в прямоугольной системе координат являются уравнениями второй степени. Такие линии называются линиями второго порядка.

1. Эллипс.

Определение 1. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть вели­чина постоянная, большая, чем рассто­яние между фокусами.

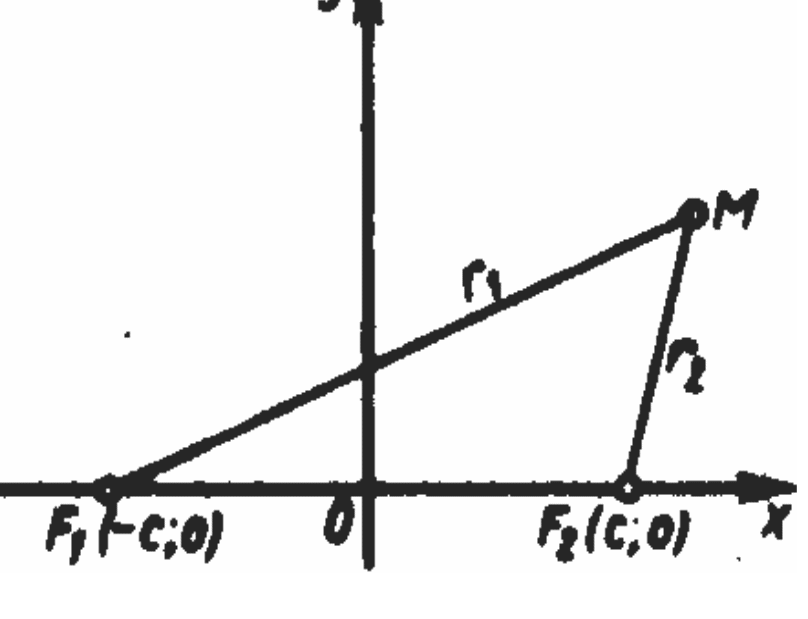
Рис. 23

Обозначим фокусы эллипса через F₁ и F₂ , расстояние

|F₁F₂| между фоку­сами через

2с, сумму расстояний от

произвольной точки эллипса до фокусов через 2a. По определению, 2а > 2с или а > с.

Вве­дем на плоскости прямоугольную сис­тему координат так, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат делило отрезок F₁F₂ пополам. Тогда фокусы имеют координаты: F₁(с; 0), F₂(c; 0) (рис. 23). Урав­нение эллипса в выбранной системе координат имеет вид

(1)

Исследуем теперь форму эллипса по его каноническому урав­нению (1). Заметим, что уравнение (1) содержит только члены с четными степенями координат х и у, поэтому эллипс симметричен относительно осей Ох и Оу, а также относительно начала коорди­нат. Таким образом, можно узнать форму всего эллипса, если установить вид той его части, которая лежит в первом координатном угле. Для этой части у ≥ 0, поэтому, разрешая уравнение (1) относи­тельно у, получаем

. (2)

Из равенства (2) вытекают следующие утверждения.

1) Если х = 0, то у = b. Следовательно, точка (0; b) лежит на эллипсе. Обозначим ее через В.

2) При возрастании х от 0 до а ордината у уменьшается.

3) Если х = а, то у = 0. Следовательно, точка (а; 0) лежит на эллипсе. Обозначим ее через A.

4) При х > а получаем мнимые значения у. Следовательно, точек эллипса, у которых х > а, не существует.

Итак, частью эллипса, расположенной в первом координатном угле, является дуга ВА (рис. 24). Произведя симметрию относительно координатных осей, по­лучим весь эллипс.

З а м е ч а н и е. Если а = b, то уравнение (1) принимает вид Это уравнение окружности радиуса а. Таким обра­зом, окружность  частный случай эл­липса. Заметим, что эллипс можно по­лучить из окружности радиуса а, если сжать ее в а/b раз вдоль оси Оу. При таком сжатии точка (х,у) перейдет в точку (х; y₁), где у₁= у (b/a). Подставляя у = у₁(a/b) уравнение окружности, получаем уравнение эллипса .

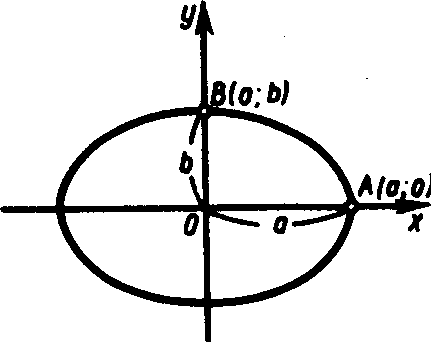
Рис. 24

Оси симметрии эллипса называются его осями, а центр симмет­рии (точка пересечения осей)  центром эллипса. Точки, в кото­рых эллипс пересекает оси, называются его вершинами. Вершины ограничивают на осях отрезки, равные 2а и 2b. Из (1) следует, что a > b. Величины а и b называются соответственно большой и малой полуосями эллипса. В соответствии с этим оси эллипса называются большой и малой осями. Введем еще одну величину, характеризующую форму эллипса.

Определение 2. Эксцентриситетом эллипса называется отноше­ние , где с  половина расстояния между фокусами, а  большая полуось эллипса.

Эксцентриситет обычно обозначают буквой ε: . Так как c < a, то 0 ≤ ε < 1 т. е. эксцентриситет эллипса меньше единицы. Принимая во внимание, что с² = a² – b², найдем

Из последнего равенства получается геометрическое истолко­вание эксцентриситета эллипса. При очень малом  числа а и b почти равны, т.е. эллипс близок к окружности. Если же  близко к единице, то число b весьма мало по сравнению с числом а, и эллипс сильно вытянут вдоль большой оси. Таким образом, эксцентриси­тет эллипса характеризует меру вытянутости эллипса.

Как известно, планеты и некоторые кометы движутся по эллип­тическим траекториям. Оказывается, что эксцентриситеты планет­ных орбит весьма малы, а кометных  велики, т.е. близки к еди­нице. Таким образом, планеты движутся почти по окружностям, а кометы то приближаются к Солнцу (Солнце нахо­дится в одном из фокусов), то значи­тельно удаляются от него.

Определение 3. Две пря­мые, перпендикулярные большой оси эллипса и расположенные сим­метрично относительно центра на расстоянии а/ε от него, на­зываются директрисами эллипса (здесь а  большая полуось, ε  эксцентриситет эллипса).

Уравнения директрис эллипса, заданного каноническим урав­нением (1), имеют вид .

Так как для эллипса ε < 1, то a/ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая  левее его левой вершины .

2. Гипербола. Определение 4. Гипер­болой называется множество всех точек плоскости, для которых модуль раз­ности расстояний от двух данных точек, называемых фокусами, есть ве­личина постоянная, меньшая, чем расстояние между фокусами.

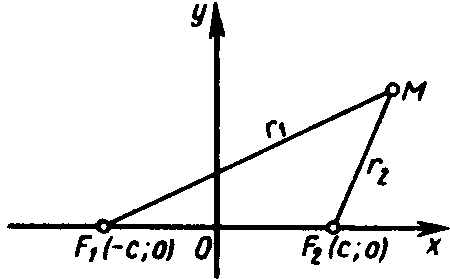
Рис. 25

Обозначим расстояние между фокусами через 2с, а модуль разности расстояний через 2а. По определению, а с.

Вве­дем на плоскости прямоугольную сис­тему координат так, чтобы фокусы гиперболы лежали на оси абсцисс, а начало координат делило отрезок F₁F₂ пополам. Тогда фокусы имеют координаты: F₁(с; 0), F₂(c; 0) (рис. 25). Урав­нение гиперболы в выбранной системе координат имеет вид

(3)

Уравнение (3) называется каноническим уравне­нием гиперболы.

Форма гиперболы исследуется по ее каноническому уравнению подобно тому, как это было сделано для эллипса.

Гипербола состоит из двух ветвей и имеет две асимптоты: и (см. рис. 26).

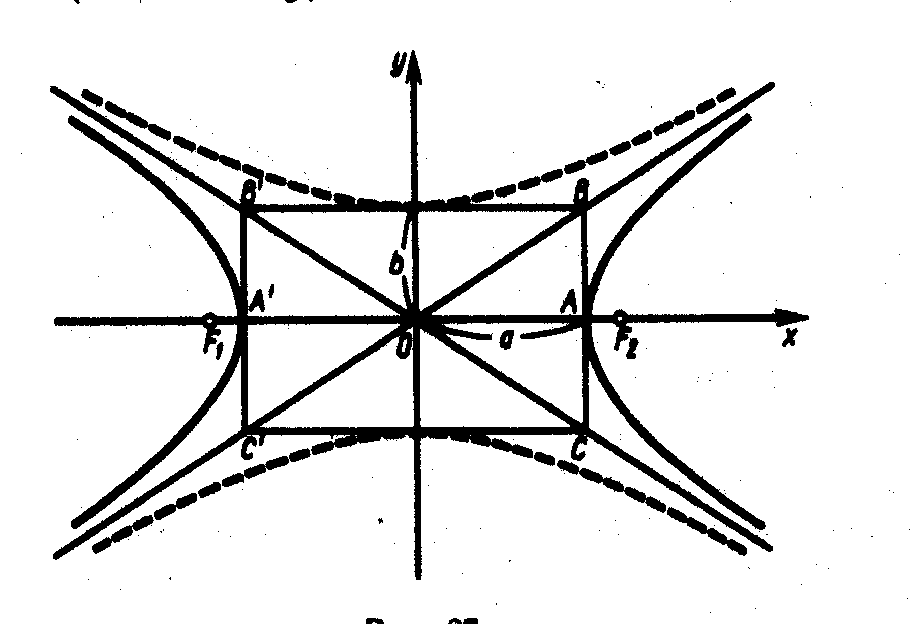
Рис. 26

Уравнение также определяет гиперболу. Она изображена на рис. 26 пунк­тирными линиями; вершины ее лежат на оси Оу. Эта гипербола называется сопряженной по отношению к гиперболе (3). Обе эти гиперболы имеют одни и те же асимптоты.

Гипербола с равными полуосями (а = b) называется равносто­ронней и ее каноническое уравнение имеет вид .

Определение 5. Эксцентриситетом гиперболы называется отно­шение , где с  половина расстояния между фокусами, а  дей­ствительная полуось гиперболы.

Эксцентриситет гиперболы (как и эллипса) обозначим буквой ε. Так как с > а, то ε > 1, т. е. эксцентриситет гиперболы больше единицы. Заметив, что , найдем , откуда .

Из последнего равенства легко получается геометрическое истол­кование эксцентриситета гиперболы. Чем меньше эксцентриситет, т.е. чем ближе он к единице, тем меньше отношение b/а, а это озна­чает, что основной прямоугольник более вытянут в направлении действительной оси. Таким образом, эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а значит, и форму самой гиперболы.

В случае равносторонней гиперболы (а = b) ε = .

Определение 6. Две пря­мые, перпендикулярные действительной оси гиперболы и расположенные сим­метрично относительно центра на расстоянии а/ε от него, на­зываются директрисами гиперболы (здесь а  действительная полуось, ε  эксцентриситет гиперболы).

Уравнения директрис гиперболы, заданной каноническим урав­нением (3), имеют вид .

Так как для гиперболы ε > 1, то a/ε < a. Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной.