
Учебное пособие 553
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
328 - 2014
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность»,
профили «Защитавчрезвычайныхситуациях», «Безопасностьжизнедеятельностивтехносфере», «Защитаокружающейсреды», очной формы обучения
Воронеж 2014
Составитель канд. физ.-мат. наук И.Н. Пантелеев
УДК 681.3.06
Функции нескольких переменных: методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность», профили «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды», очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев. Воронеж, 2014. 41с.
Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" при изучении во 2 семестре раздела «Функции нескольких переменных» для студентов специальности ТБ. В работе приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.
Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и
содержатся в файле Vmfmm_FNPMeT _1.pdf.
Ил.1. Библиогр.: 6 назв.
Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский государственный технический университет», 2014
1. Понятие функции двух переменных. Область определения
Переменная величина z называется функцией двух переменных величин x и y, если каждой паре допустимых значений x и y соответствует единственное значение z. Функция двух переменных обозначается символом: z = f (x, y)
или z = z( x, y).
Систему значений x и y называют точкой М( x, y), а функцию двух переменных – функцией точки z = f (М).
Геометрическим изображением функции двух переменных является некоторая поверхность в пространстве.
Значение функции z = f (x, y) при x = a, y = b обозначается через f ( a, b).
Совокупностью всех точек, в которых определена функция двух переменных, называется областью существования или областью определения функции и является некоторая часть координатной плоскости, ограниченная одной или несколькими линиями ( или вся плоскость).
Пример 1 . Найти область определения функций:
1) z = xy ; 2) z = |
1 |
|
; |
|
|
||
|
9 x 2 |
y 2 |
|
Решение: 1) Данная функция определена, когда подкоренное выражение неотрицательно, т. е. xy ≥ 0. Это
возможно в двух случаях: 1) x 0, y 0; 2) x 0, y 0. Первому условию удовлетворяют координаты всех точек, лежащих в первой четверти и на координатных осях, второму
– координаты точек, лежащих в третьей четверти и на координатных осях. Следовательно, область определения – совокупность точек, расположенных в первом и третьем координатных углах и на координатных осях.
2) Функция определена, когда подкоренное выражение положительно, т. е. 9 – x2 – y2 > 0 или x2 + y2 < 9. Последнему неравенству удовлетворяют точки, лежащие внутри круга радиуса R =3 (граничные точки исключаются). Область
определения функции – совокупность точек, лежащих внутри круга радиуса R = 3 с центром в начале координат.
Линией уровня функции z = f (x, y) называется геометрическое место точек плоскости xOy, для которых данная функция имеет одно и тоже значение: уравнение линии уровня есть f (x, y) = с.
2. Частные производные и полный дифференциал функции двух переменных
Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю.
Для функции z = f (x, y) по определению имеем:
z |
= |
f x' (x , y) = lim |
f (x x, y) f (x, y) |
(частная |
x |
|
|||
|
x 0 |
x |
||
производная по x),
z |
f y' (x, y) lim |
f (x, y y) f (x, y) |
(частная |
|
y |
y |
|||
y 0 |
|
производная по y).
При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая другой аргумент постоянным.
Полный дифференциал функции z = f (x, y) вычисляется по формуле
dz = xz dx yz dy .
Функция, имеющая полный дифференциал, называется
дифференцируемой.
2
П р и м е р 2. Найти частные производные функции z x2 2xy y3 .
Решение: Считая y постоянной и дифференцируя z как функцию x, получаем частную производную по x:
z |
(x 2 )'x (2xy)'x ( y 3 )'x 2x 2 y 0 2(x y). |
x |
|
Аналогично, считая x постоянной и дифференцируя z как функцию y, получаем частную производную по y:
z |
(x 2 )'y (2xy)'y ( y3 )'y 0 2x 3y 2 . |
y |
|
|
3. Дифференцирование неявных функций |
Функция двух переменных называется неявной, если она задана уравнением F (x , y, z) = 0, не разрешенным относительно z.
Производные неявной функции находятся по формулам:
z |
|
|
F ' |
z |
|
|
Fy' |
|
|
||
|
|
x |
, |
|
|
|
|
|
. |
|
|
x |
|
y |
|
Fz' |
|
||||||
|
|
Fz' |
|
|
|
|
|||||
4. Экстремум функции двух переменных |
|
||||||||||
Максимумом (минимумом) функции |
z = |
f (x, y) |
|||||||||
называется такое ее |
значение |
f (x0, |
y0), |
которое |
больше |
||||||
(меньше) всех других значений, принимаемых ею в точках, достаточно близких к точке M0 (x0, y0) и отличных от нее.
Максимум или минимум функции называется ее экстремум. Точка, в которой достигается экстремум,
называется точкой экстремума.
Экстремум функции может достигаться лишь в точках, лежащих внутри области ее определения, в которых все частные производные первого порядка обращаются в нуль. Такие точки называются критическими. Для функции z = f (x, y) критические точки находятся из системы уравнений:
3

fx (x, y) 0,f y (x, y) 0.
Условия являются необходимыми условиями
экстремума. Достаточные условия экстремума выражаются с помощью определителя
BA CB AC B 2 ,
где
А = f”xx(x0 , y0), B = f”xy (x0 , y0), C = f”yy(x0 , y0),
а именно: |
|
|
1) если >0, то |
M0 (x0, |
y0) – точка экстремума: при |
А<0 (или C<0) – точка максимума, при A>0 (или C >0) – точка |
||
минимума, |
|
|
2) если < 0, то в точке M0 нет экстремума. |
||
Если = 0, то |
вопрос |
о наличии или отсутствии |
экстремума функции остается открытым (требуется дальнейшее исследование функции).
Пример 3. Исследовать на экстремум функцию z = x3 + y3 + 9xy.
Решение. Находим частные производные первого и второго порядка:
f’x( x, y) = 3x2 + 9y; f’y ( x, y) = 3y2 + 9x;
f”xx ( x, y) = 6x; f”xy ( x, y) = 9; f”yy ( x, y) = 6y.
Приравнивая к нулю первые производные, получим систему уравнений для определения критических точек:
3x 2 9y 0,
3y 2 9x 0.
Решая систему находим две критические точки
М1 (0, 0), М2 ( –3, –3).
4
Вычисляем значения частных производных второго порядка в этих точках:
А1 = fxx ( 0, 0) = 0, B1 = fxy ( 0, 0) = 9, C1 = fyy ( 0, 0) = 0,
A2 = fxx (–3, –3) = –18, B2 = fxy (–3, –3) = 9, C2 = fyy (–3,–3) = – 18.
Затем находим определитель:
1 А1С1 В12 0 0 92 81;
2 А2С2 В22 ( 18) ( 18) 92 243.
Всилу достаточных условий заключаем, что в точке М1 нет
экстремума, так как 1 < |
0, |
а в точке М2 функция имеет |
максимум, так как 2 > 0 |
и А2 < 0, причем |
|
max f ( x , y) = |
f (–3, –3) = 27. |
|
5. Производная в данном направлении. Градиент функции.
Производной |
функции |
z f (x, y) в точке M (x, y) |
в |
||||||
направлении вектора |
|
|
называется предел |
|
|||||
l |
MN |
|
|||||||
|
z |
|
lim |
f (N |
) f (M ) |
. |
|
||
|
l |
|
|
|
|||||
|
|
M N |
0 |
|
M N |
|
|
|
|
|
|
|
f (x, y) |
|
|
|
|
||
Если |
функция |
|
дифференцируема, |
то |
|||||
производная в данном направлении вычисляется по формуле |
|
||||||||
|
z |
|
z cos |
z sin , |
|
||||
|
l |
|
x |
|
y |
|
|||
где – угол, образованный вектором l с осью Оx. Градиентом функции z f (x, y) в точке M (x, y)
называется вектор с началом в точке М, имеющим своими координатами частные производные функции z:
5

gradz xz i yz j.
Градиент указывает направление наибыстрейшего роста
функции в данной |
точке. Производная |
z |
в направлении |
|||||||
|
|
|
|
|
|
|
|
l |
|
|
градиента имеет наибольшее значение, равное |
|
|||||||||
|
z |
|
gradz |
|
|
z |
2 |
|
z 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
. |
||||
l наиб |
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
y |
|||||
6. Дифференциал сложной функции. Инвариантность формы первого дифференциала
Пусть дана сложная функция z = f (u,v), u =u (x, у) , v =v (x, у) и пусть все эти функции дифференцируемы. Найдем полный дифференциал сложной функции. Имеем :
|
|
|
|
|
|
|
|
dz |
z dx |
z |
dy . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||
|
|
z u |
|
z v |
|
|
z u |
|
z v |
|
|
|
|
||||||||||||
dz |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dy = |
|
|
||||
|
|
|
|
u y |
|
|
|
|
|
||||||||||||||||
|
|
u x |
|
v x |
|
|
|
v y |
|
|
|
|
|||||||||||||
z |
u |
|
|
u |
|
|
z |
v |
|
|
v |
|
|
|
z |
du |
z |
dv . |
|||||||
|
|
|
|
dx |
|
|
dy dx |
|
|
|
|
dx |
|
|
dy |
= |
|
|
|||||||
|
x |
y |
x |
y |
u |
v |
|||||||||||||||||||
u |
|
|
|
|
v |
|
|
|
|
|
|
|
|||||||||||||
Таким образом, dz uz du vz dv .
То есть формула для дифференциала первого порядка такая же, как и для случая, когда u и v независимые переменные.
Следовательно, форма записи дифференциала первого порядка не зависит от того, являются ли u и v независимыми переменными или функциями. Это свойство называется инвариантностью.
6
7.Метод наименьших квадратов
Вразличных исследованиях приходится использовать формулы, составленные на основании эксперимента. Одним из лучших способов получения таких формул является метод наименьших квадратов.
Пусть на основании эксперимента необходимо установить функциональную зависимость между двумя переменными величинами х и у. Например, между температурой и удлинением прямолинейного металлического стержня. По результатам измерений составим следующую таблицу:
х |
х1 |
х2 |
… |
хi |
… |
|
xn |
|
у |
у1 |
у2 |
… |
yi |
… |
|
yn |
|
Установим теперь вид функции у = f(x) |
по характеру |
|||||||
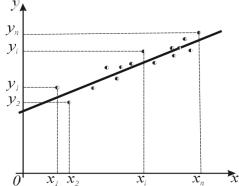
расположения на координатной плоскости экспериментальных точек. Пусть, например, точки, взятые из таблицы, расположены так, как показано на рис.1. В данном случае естественно предположить, что между х и у существует линейная зависимость, выражающаяся формулой
y = ax + b |
(1) |
Рис.1
7
Ограничимся только случаем линейной зависимости. Так как точки (х1 ; у1), (х2 ; у2),….,( хn ; уn ) не лежат точно на прямой, а лишь вблизи нее, то формула (1) является приближенной. Поэтому, подставляя значения координат точек в выражение у – (ах+b), получаем равенства
у1 – (ах1 + b ) = δ1, у2 – (ах2 + b ) = δ2 , … , уn – (axn + b) =
δn,
где δ1, δ2,…., δn – некоторые числа, которые назовем погрешностями.
Поставим задачу подобрать коэффициенты а и b таким образом, чтобы эти погрешности были возможно меньше по абсолютной величине. Для решения этой задачи воспользуемся методом наименьших квадратов. Рассмотрим сумму квадратов погрешностей.
n
S(a,b) y1
i 1
(axi b) 2 |
n |
i2 . |
|
|
i 1 |
Здесь хi и yi – заданные числа, а коэффициенты а и b – неизвестные числа, подлежащие определению, исходя из условий минимума S(a, b), т.е. S(a, b) можно рассматривать как функцию двух переменных a и b и исследовать ее на экстремум.
Таким образом, задача свелась к нахождению значений а и b, при которых функция S(a, b) имеет минимум. Имеем
S |
n |
S |
n |
2 yi (axi b) xi , |
2 yi (axi b) . |
||
a |
i 1 |
b |
i 1 |
Приравнивая эти частные производные к нулю, получаем линейную систему двух уравнений с двумя неизвестными a и b:
8
|
n |
n |
n |
|
|
yi xi a xi2 |
xi , |
|
|
|
i 1 |
i 1 |
i 1 |
(2) |
n |
n |
|
||
|
|
|
||
|
yi a xi bn. |
|
||
|
i 1 |
i 1 |
|
|
Система (2) называется нормальной системой метода наименьших квадратов. Из этой системы находим числа a и b и затем, подставляя их в уравнение (1) , получаем уравнение искомой прямой.
Тот факт, что функция S(a,b) в найденной точке М(a; b) имеет минимум, легко устанавливается с помощью частных производных второго порядка. Имеем
|
|
|
2 S |
n |
2 |
|
2 S |
|
n |
2 S |
|
|
|
|
|||||
|
|
|
2 2 xi , |
|
|
|
2 xi , |
|
|
2 |
|
2n. |
|
||||||
|
|
|
|
a b |
|
|
|
|
|||||||||||
|
|
|
a |
i 1 |
|
|
|
|
|
|
i 1 |
b |
|
|
|
|
|
||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 S 2 S |
|
2 S 2 |
|
n |
2 |
|
|
|
n |
|
2 |
|||||
|
|
|
a2 b2 |
|
|
|
|
|
4n xi |
|
|
2 xi . |
|||||||
|
|
|
|
||||||||||||||||
|
|
|
|
a b2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
i 1 |
|
|
||
|
Это |
|
выражение |
|
можно |
записать |
в |
виде |
|||||||||||
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (xi x j |
)2 , |
|
откуда |
следует, |
что |
>0. |
Так как |
|||||||||||
2 S |
i 1 i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0, |
то в точке |
М (a; |
b) функция S (а, b) имеет минимум. |
||||||||||||||||
a2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. Индивидуальные задания для контрольной работы Вариант 1
9
