6. Дифференцирование сложной функции.

Теорема 3. Если функция x=(t) имеет производную в точке t₀, а функция y = f(x) имеет производную в соответствующей точке x₀ =  (t₀), то сложная функция f((t)) имеет производную в точке t₀ и справедлива следующая формула: y (t₀) = f  (x₀) (t_o).

З а м е ч а н и е 1. В данной теореме рассмотрена сложная функция, где у зависит от t через промежуточную переменную х. Возможна и более сложная зависимость  с двумя, тремя и боль­шим числом промежуточных переменных, но правило дифференци­рования остается таким же.

Так, например, если у = f(х), где x = (u), a u = (v) и v = (t), то производную у (t) следует вычислять по формуле у (t) = f(х)(u)(v)(t).

Пример 1. Вычислить производную функции

Р е ш е н и е. Данную функцию можно представить в виде у = е^u, где u = arctg x. Тогда по правилу дифференцирования сложной функции

у' (х) = у' (и) и' (х) =

Заменяя и на arctg x, окончательно получим

Пример 2. Вычислить производную функции

Р е ш е н и е. Данную функцию можно представить в виде у = и², где u = tg v, a и w = x² + 1. По правилу дифференцирования сложной функции получаем

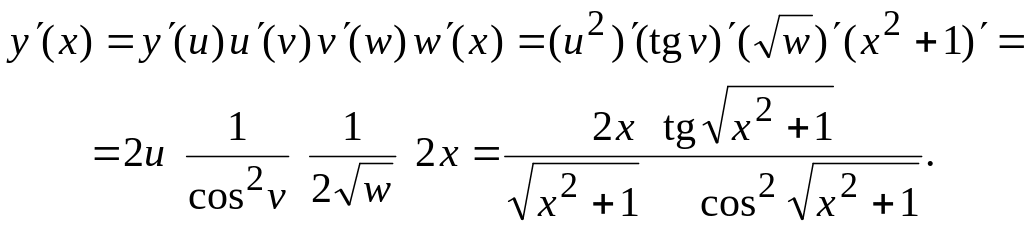
З а м е ч а н и е 2. Иногда производную приходится вычислять непосредственно исходя из ее определения. Найдем, например, производную функции

При x  0 производная вычисляется по формулам и правилам дифференцирования:

Этим выражением нельзя воспользоваться при х = 0. В точке х = 0 производную можно вычислить, используя определение производной:

т.к. произведение бесконечно малой функции на ограниченную есть бесконечно малая. Таким образом,

Теорема 4 (инвариантность формы дифференциала). Дифференциал функции у выражается по одной и той же формуле независимо от того, будет ли у рассматриваться как функция от независимой переменной х, или от зависимой переменной х.

7. Логарифмическая производная. Производная степенной функции. Вычислим производную функции у = ln |x| ( x  0 ). Так как (1n х) = и (ln(х)) = (последнее равенство получено на основании правила дифференцирования сложной функции), то производная данной функции выражается следующей формулой

Учитывая эту формулу, вычислим производную сложной функции у = ln |u|, где u = f(x)  дифференцируемая функция. Имеем

или

Производная (1n|f(х)|) называется логарифмической произ­водной функции f(х). Для упрощения записи при логарифмическом дифференцировании знак модуля у функции f(х) обычно опуска­ется.

Вычислим с помощью логарифмической производной производ­ную показательно-степенной функции у = , где и и v – некоторые функции от х ( и > 0 ), имеющие в данной точке х про­изводные и (х) и v (х). Так как ln у = v(х) ln и(х), то имеем

Отсюда, учитывая, что у = , получаем следующую фор­мулу для производной показательно-степенной функции:

Пример. Вычислить производную функции y = .

Р е ш е н и е. Данную функцию можно представить в виде у = , где u(х) = х и v (х) = х. Поэтому

Логарифмическая производная очень удобна при нахождении производной степенной функции с любым вещественным показа­телем.

Производная степенной функции с любым действительным по­казателем (  любое веществен­ное число) выражается формулой

8. Таблица производных простейших элементарных функций. Нами вычислены производные всех простейших элементарных функций и мы можем составить следующую таблицу производных.

I. (С) = 0.

II. в частности

III. (log_а х) = log_а е, в частности (ln х) = .

IV. в частности,

V. (sin х) = cos х.

VI. (cos х) =  sin х.

vii. (tg x) =

VIII. (ctg x)=

IX. (arcsin х) = .

X. (arccos x) = .

XI. (arctg x) = .

12. (arcctg x) = .

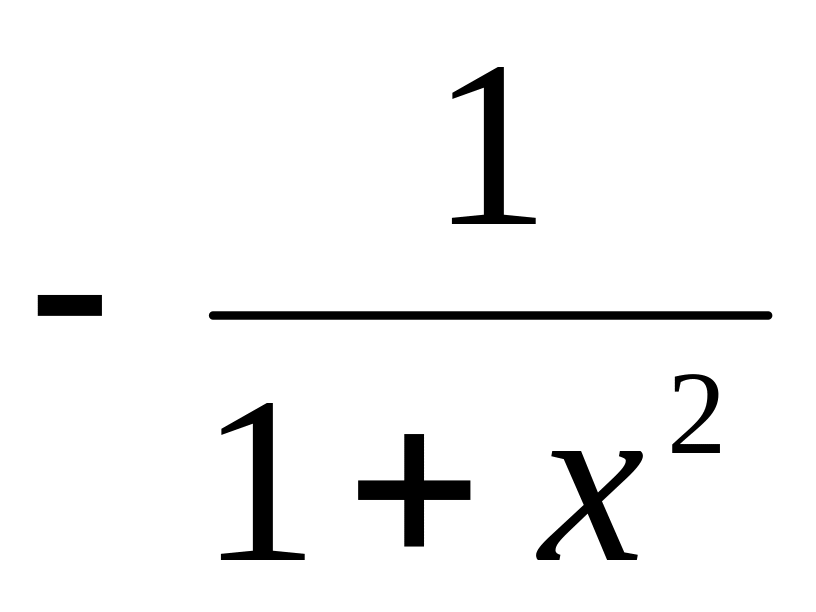XIII. (sh х) = ch х.

XIV. (ch х) = sh х.

15. (th x) =

XVI. (cth x) =

Формулы, приведенные в таблице, а также правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.