5. Предел последовательности

5.1. Числовые последовательности

1. Числовые последовательности и арифметические действия над ними. Числовые последовательности изучают уже в школе. Примерами таких последовательностей могут служить: 1) последовательность всех членов арифметической и геометрической прогрессий; 2) последовательность периметров правильных п-угольников, вписанных в данную окружность; 3) последовательность х₁ = 1, х₂ = 1,4, х₃ = 1,41… приближенных значений . Уточним и расширим понятие числовой последовательности.

Определение. Если каждому числу п из натурального ряда чисел 1, 2, 3, … , п, … поставлено в соответствие действительное число х_п , то множество действительных чисел х₁, х₂ , х₃ , …, х_n , … называется числовой последовательностью или просто последовательностью.

Числа х₁, х₂ , х₃ , …, х_n ,… будем называть элементами (или членами) последовательности, символ х_n – общим элементом (или членом) последовательности, а число п – его номером. Сокращенно последовательность будем обозначать символом {х_n}. Так, например, символ обозначает последовательность

Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула задает последовательность: 0, 2, 0, 2 … Обращая дробь в десятичную и оставляя один, два, три и т. д. знака после запятой, получим последовательность

По самому определению, последовательность содержит бесконечное число элементов: любые два ее элемента отличаются, по крайней мере, своими номерами.

Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам

последовательности. На рис. 41 изображены соответственно последовательности

1

0 х₄ х₃ х₂ х₁ х

1

х₁ х₃ х₅ х₇ 0 х₆ х₄ х₂ х

Рис. 41

Введем арифметические действия над числовыми последовательностями. Пусть даны последовательности {х_n} и {y_n}.

Произведением последовательности {х_n} на число m назовем последовательность mх₁ , mх₂ , …, mх_n , …;

cуммой данных последовательностей назовем последовательность х₁у₁ , х₂у₂ , …., х_пу_п , …;

разностью – последовательность х₁у₁ , х₂ у₂ , …., х_nу_n , …;

произведением – последовательность х₁у₁ , х₂у₂ , …., х_nу_n , …;

частным – последовательность 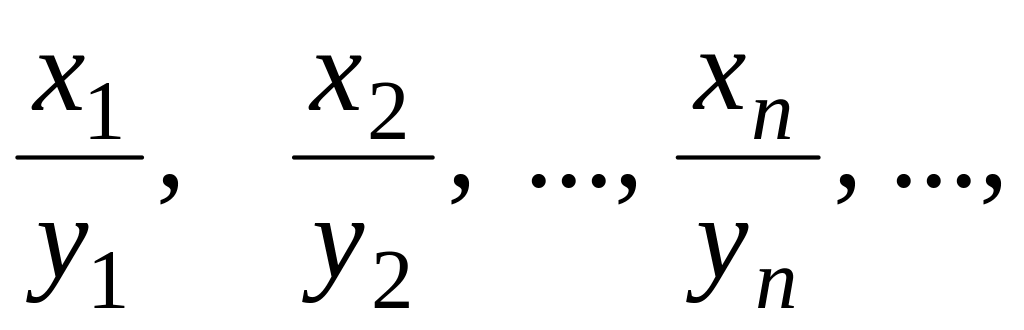если все члены последовательности {y_n} отличны от нуля.

2. Ограниченные и неограниченные последовательности.

Определение 1. Последовательность {х_п} называется ограниченной сверху (снизу), если существует число М (число m) такое, что любой элемент х_п этой последовательности удовлетворяет неравенству

Определение 2. Последовательность {х_п} называется ограниченной, если она ограничена и сверху и снизу.

Пусть Тогда условие ограниченности последовательности можно записать в виде

Определение 3. Последовательность {х_п} называется неограниченной, если для любого положительного числа А существует элемент х_п этой последовательности, удовлетворяющий неравенству